Johann Carl Friedrich Gauß, der Zahlenmann
In den ersten Jahrzehnten des 19. Jahrhunderts bestimmten die Seeleute den Breitengrad entweder nach der Mittagsbreite oder Nordsternbreite mit anschließender Koppelnavigation oder nach der Douw’schen Methode. Um den Längengrad bestimmmen zu können, musste man Monddistanzen zu anderen Himmelskörpern messen und daraus die Zeit am Nullmeridian berechnen, wozu zahlreiche Tabellen zur Verfügung standen. Eine einmal gefundene Breite, egal nach welcher Methode, musste bis zu einer neuen Breitenbestimmung oder Standortbestimmung unter Berücksichtigung von Fahrgeschwindigkeit, Kurs und Abdrift gekoppelt werden. Nachdem gegen Ende des 18. Jahrhunderts das Chronometer erfunden war, begann dessen Serienfertigung, doch es sollte noch lange dauern, bis alle Schiffe mit einem Chronometer ausgerüstet werden konnten.
Johann Carl Friedrich Gauß war ein deutscher Mathematiker, Statistiker, Astronom, Geodät, Physiker und Elektrotechniker. Wegen seiner überragenden wissenschaftlichen Leistungen galt er bereits zu seinen Lebzeiten als „Princeps mathematicorum“. Gauß leitete in den Jahren 1821 – 1825 die Vermessung des Königreiches Hannover. Doch sein Interesse an der Landvermessung war schon viel früher vorhanden. Zwischen 1802 und 1807 führte er trigonometrische Vermessungen unter anderem weit über das Stadtgebiet von Braunschweig hinweg aus. Dabei benutzte er einen Sextanten, den er sich von seinem Freund Franz Xaver von Zach auslieh. Unter Anwendung der von ihm selbst entwickelten Methode der kleinsten Quadrate konnte er Beobachtungsfehler minimieren und auf diese Weise sehr präzise Messungen anstellen.
Im Jahre 1807 wurde Gauß zum Universitätsprofessor und Sternwartendirektor in Göttingen berufen. Die Sternwarte wurde allerdings erst 1816 fertiggestellt. Neben der Mathematik und seinen Landvermessungen war natürlich auch Astronomie ein Gebiet, auf dem sich Gauß überaus gerne bewegte. Überhaupt war damals die Astronomie ein sehr populärer Wissenschaftszweig.
Gauß war kein Seemann, doch eine Ortsbestimmung auf See unterscheidet sich nicht wirklich von einer Ortsbestimmung an Land. Schließlich muss auch ein Kartograf Längen- und Breitengrade auf seinen Landkarten einzeichnen können. So war die Dissertation eines Herrn Kraft für Gauß der Anlass für eine bemerkenswerte Arbeit, mit der er gleichzeitig auch eine Lösung des Zweihöhenproblems der Seefahrer lieferte. In seiner Arbeit beschreibt W. Kraft, wie aus der gemessenen Höhe zweier Sterne die geografische Breite berechnet wird.
Seine Arbeit basierte auf dem, damals jedem Astronomen bekannten, Modell mit den zwei bekannten Sternpositionen X und X’, dem zu bestimmenden Scheitelpunkt Z und dem Nordpol P, wie es das Bild zeigt. Doch erstmalig gab es einen entscheidenden Unterschied. Herr Kraft stützte sich nicht auf das grafische Modell, sondern auf ein Gleichungssystem, in das er die Zeichnung zuvor verwandelt hatte und diese damit mathematisch exakt mit zwei verbundenen Gleichungen beschrieb. Diese Transformation von einem allgemein verständlichen Bild in eine abstrakte mathematische Form war ein völlig neuer Ansatz.
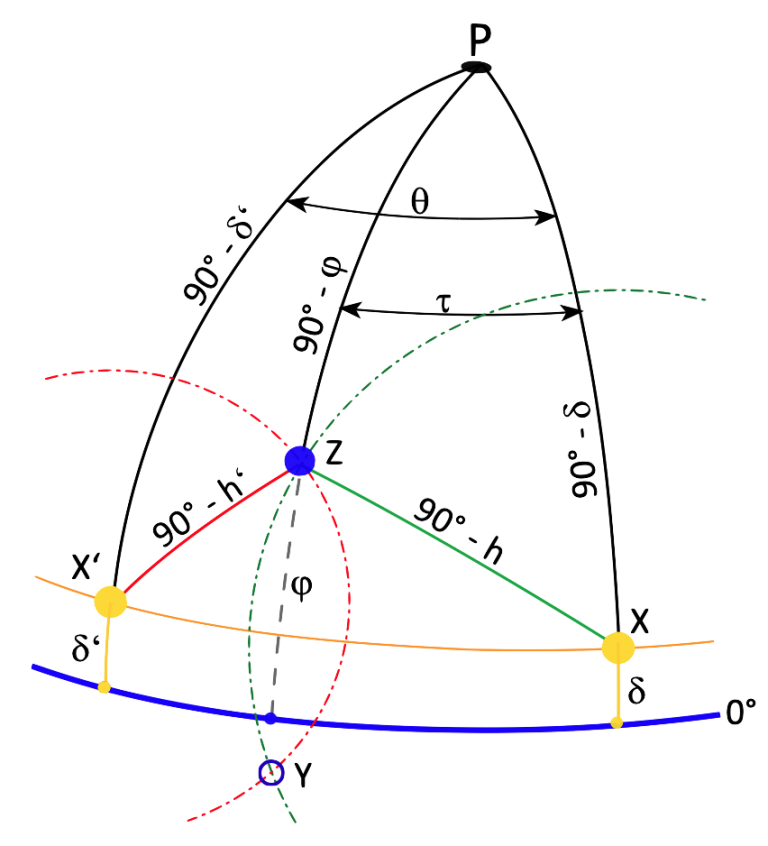
An einer gezeichneten Sache entsteht visueller Kontakt mit einem Problem und es fällt sehr viel leichter, an solch einem Modell Lösungswege zur Berechnung noch unbekannter Elemente aus den vorhandenen bekannten Elementen zu entwickeln. So kann man Schritt für Schritt echte Elemente oder Teile eines solchen Modells berechnen und dabei verschiedene Lösungswege ausprobieren, bis man auf eine gewünschte oder annehmbare Lösung kommt. Das ist die Arbeitsweise eines Ingenieurs. Herr Kraft war aber kein Ingenieur, sondern Mathematiker und hat deshalb die Bildsprache, die eine Zeichnung vermittelt, in seine abstrakte mathematische Sprache übersetzt.
Er stellte für die beiden Dreiecke XPZ und X’PZ ein Gleichungssystem mit zwei Unbekannten auf, welche in diesem Fall die Breite ![]() und der Stundenwinkel
und der Stundenwinkel ![]() sind. Damit, dachte er, müssen nicht mehr einzeln und nacheinander Strecken und Winkel berechnet werden, um das Ziel zu erreichen, man müsse jetzt nur das Gleichungssystem auflösen und hätte das Ergebnis.
sind. Damit, dachte er, müssen nicht mehr einzeln und nacheinander Strecken und Winkel berechnet werden, um das Ziel zu erreichen, man müsse jetzt nur das Gleichungssystem auflösen und hätte das Ergebnis.
Herrn Kraft ist es zwar gelungen, beides zu berechnen, jedoch in einer ziemlich verwickelten Auflösung. Gauß bemerkte dazu, dass es stattdessen einfacher wäre, die Breite durch direkte Betrachtung dreier Dreiecke zu finden (siehe hier). Außerdem fand er die spezielle Einschränkung von Herrn Kraft sonderbar, dass die Höhen der beiden Sterne zum selben Zeitpunkt gemessen werden müssen. Das hätte zwei Meßwerkzeuge und zwei Beobachter gleichzeitig erfordert. Die Sonne würde dann als Navigationsgestirn sogar ausscheiden, weil sie zur selben Zeit nur eine Höhe besitzen kann. Gerade der Sonne maß Gauß eine besondere Bedeutung zu, denn sie scheint am Tag und der Winkel am Sextanten ist bei Tageslicht viel besser abzulesen.
Gauß erkannte den Vorteil, den dieser neue mathematische Ansatz für die Arbeit in der Kartographie und für die Seefahrer bedeuten konnte. So machte er sich daran, mit dem Ansatz des Herrn Kraft eine eigene und bessere Lösung zu erarbeiten. Das Ergebnis seiner Arbeit erschien im Jahre 1809 in „Bodes Astronomisches Jahrbuch“ für das Jahr 1812 unter dem Titel:
„ Neue Methode, aus der Höhe zweier Sterne die Zeit und die Polhöhe zu bestimmen, nebst astr. Beobachtungen, von Herrn Professor Gauß in Göttingen.“
Es hätte eine Sternstunde in der Hochseenavigation sein können und Gauß selbst war davon überzeugt, eine Methode gefunden zu haben, die für praktische Anwendungen endlich geeignet sei, doch er sollte sich irren. Tatsächlich ermöglichte sein Formelapparat eine präzise Berechnung des Breitengrades und der Zeit und das sogar mit Logarithmen innerhalb vertretbarer Zeit, doch das war nicht das Problem. Seine Auflösung bestand letzlich aus Substitutionen, die er mit V, W, und G bezeichnete, die jedoch keinem einzigen Element aus der Praxis oder dem bekannten Grafikmodell zugeordnet werden konnten. Zwar konnten mit diesen Substitutionen Breite und Zeit und aus der Zeit die Länge ganz einfach errechnet werden, doch niemand konnte daraus eine Vorstellung entwickeln. Sein Lösungsweg war nicht vermittelbar. Gauß war seiner Zeit viel zu weit voraus und Mathematik passte auch ein Jahrhundert nach Douwes noch immer nicht zum Handwerk eines Seemannes.
Die Methode von Gauß
Gauß hat zu seinen Lebzeiten relativ zurückhaltend publiziert. Die meisten seiner Arbeiten stammen aus einem Nachlass, den ein Urenkel lange nach seinem Tod entdeckt und der Wissenschaft zugänglich gemacht hat. Deshalb ist es verwunderlich, dass gerade diese Arbeit publiziert wurde. Seine Lösung war nicht nur ein Meilenstein in der Historie der astronomischen Navigation, der als solcher allerdings nicht erkannt wurde, sondern aus heutiger Sicht sogar ein Juwel. Es existiert kein Verfahren, das sich besser digitalisieren läßt und somit als App oder Computerprogramm zur Navigation mit einem Sextanten benutzt werden kann. Die Gauß’sche Methode, wie sie in Bodes astronomischem Jahrbuch publiziert wurde, soll deshalb nachfolgend im Original wiedergegeben werden. Gestartet wird mit dem Gleichungssystem, das W. Kraft von dem gezeichneten Modell abgeleitet hat. Die Terminologie im Text und in den Formeln sind dabei weitgehend unserem heutigem Verständnis angepasst.
Hiernach beruht also die Auflösung dieses Problems auf der Entwicklung folgender beider Gleichungen:
(1) ![]()
(2) ![]()
(Anmerkung ![]() : In Grad verwandelte Zeit zwischen den Beobachtungen.)
: In Grad verwandelte Zeit zwischen den Beobachtungen.)
Die Eliminierung einer der beiden unbekannten Größen ![]() oder
oder ![]() würde auf eine sehr verwickelte Gleichung führen. Herr Kraft hat in seiner Dissertation diesen Weg gewählt, aber seine Auflösung ist meiner Meinung nach ungleich weitläufiger und mühsamer als diejenige, welche unmittelbar aus der Betrachtung dreier Dreiecke hervorgeht, obgleich sie sich bloß auf die Bestimmung von
würde auf eine sehr verwickelte Gleichung führen. Herr Kraft hat in seiner Dissertation diesen Weg gewählt, aber seine Auflösung ist meiner Meinung nach ungleich weitläufiger und mühsamer als diejenige, welche unmittelbar aus der Betrachtung dreier Dreiecke hervorgeht, obgleich sie sich bloß auf die Bestimmung von ![]() einschränkt, und sich auf die Bestimmung der Zeit nicht einlässt. Es ist daher besser, beide,
einschränkt, und sich auf die Bestimmung der Zeit nicht einlässt. Es ist daher besser, beide, ![]() und
und ![]() mit Hilfe einer neuen unbekannten Größe zu eliminieren. Es ist nämlich offenbar:
mit Hilfe einer neuen unbekannten Größe zu eliminieren. Es ist nämlich offenbar:
![]()
![]()
und daher zufolge der Gl. 1:
![]()
Man kann daher setzen:
(3) ![]()
(4) ![]()
Verbindet man nun die Gleichungen 3 und 1, so folgt:
(5) ![]()
(6) ![]()
Man gebe ferner der Gleichung 2 folgende Gestalt:
![]()
und setze für sin 𝜑, cos 𝜑 ⋅ cos 𝜏 und cos 𝜑 ⋅ sin 𝜏 ihre Werte aus den Gln. 5, 6 und 4, so findet sich:
![]()
![]()
Diese Gleichung verwandelt sich, wenn man setzt:
(7) ![]()
in Folgende:
![]()
![]()
Macht man ferner V – U = W , so hat man:
(8) ![]()
Woraus also W und auch U = V – W bekannt wird.
Nachdem der Winkel U gefunden worden ist, lässt sich nun auch ![]() aus der Verbindung der Gleichungen 4 und 6 leicht herleiten, woraus sich ergibt:
aus der Verbindung der Gleichungen 4 und 6 leicht herleiten, woraus sich ergibt:
(9) ![]()
Ist aber ![]() bekannt, so ergibt sich auch
bekannt, so ergibt sich auch ![]() , und wenn man diesen Winkel in Zeit verwandelt, so hat man den Stand der Uhr. Aus der Verbindung der Gleichungen 4 und 5 ergibt sich:
, und wenn man diesen Winkel in Zeit verwandelt, so hat man den Stand der Uhr. Aus der Verbindung der Gleichungen 4 und 5 ergibt sich:
(10) ![]()
Mit dieser Formel kann man noch die Gleichung 4 verbinden, so hat man zugleich eine Kontrolle, wodurch die Richtigkeit der Rechnung geprüft wird.
Über die im voranstehenden Teil gelehrte Auflösung bemerke ich noch folgendes: da der Winkel W nach der Formel 8 durch die Kosinus gefunden wird, so sind für ihn zwei Werte, ein positiver und ein negativer möglich und die Aufgabe lässt mithin eine doppelte Auflösung zu, wie bereits oben bemerkt worden ist: …
Übrigens lässt sich die vorhin gegebene Auflösung auch noch etwas abkürzen und für die numerische Entwicklung durch Einführung zweier Hilfswinkel bequemer einrichten. Setzt man nämlich:
(11) ![]()
so verwandeln sich die Gleichungen 9 und 10 in die folgenden:
(12) ![]()
(13) ![]()
(Anmerkung: P = +1wurde hinzugefügt, P = -1 berechnet den südlichen Schnittpunkt)
Ferner nenne man einen zweiten Hilfswinkel G, und mache:
(14) ![]()
So verwandeln sich die Gleichungen 9 und 10 in die folgenden:
(15) ![]()
(16) ![]()
(17) ![]()
Die praktischen Astronomen pflegen sich nicht selten zu beschweren, dass die von den Theoretikern vorgeschlagenen Methoden zu wirklichen Anwendung nicht immer ganz geeignet sein, oder wenigstens nicht vollkommen leisten, was sie sich von Ihnen versprechen. Dass dieser Vorwurf die hier vorgetragenen Methode nicht treffe, wird das folgende Beispiel hinlänglich dartun, wozu ich die Data aus wirklich angestellten Beobachtungen entlehne. Mit einem Troughton’schen Sexstanten von 10 Zoll fand ich am 21. August 1808 die doppelte und verbesserte Höhe von ![]() im Adler …”
im Adler …”
Die letzte Gleichung liefert auch gleich die Standortlänge. Bei ![]() handelt es sich um Westlängen, sofern der Wert kleiner als 180° ist, ist er größer als 180°, dann muss er von 360° subtrahiert werden und es sind Ostlängen.
handelt es sich um Westlängen, sofern der Wert kleiner als 180° ist, ist er größer als 180°, dann muss er von 360° subtrahiert werden und es sind Ostlängen.
Soweit die Wiedergabe der einzigen Übersetzung der Publikation von Carl Friedrich Gauß, die als Original im lateinischen abgefasst war. Gauß hat argumentiert, dass diese Methode für die Praxis geeignet sei, weil damit in wenigen Minuten ein Standort berechnet werden kann, ohne dass dazu besondere mathematische Kenntnisse nötig wären. Seine Formeln von Gl. 11 bis 17 hat er auch so zugeschnitten, dass sie mit Logarithmen leicht lösbar sind. So kommen praktisch nur Multiplikationen und Divisionen vor, was im Bildbereich der Logrithmenrechnung nur noch Additionen und Divisionen sind.
Doch die Gauß Formeln erreichten die Seefahrt nicht. Sie hätten den Seefahrern auch nicht geholfen. Woran sollte man überhaupt erkennen können, dass ein Ergebnis richtig ist? Bei dem Schritt für Schritt Verfahren über die Dreiecke hätte man wenigstens eine ungefähre Orientierung, ob die Zwischenergebnisse noch von dieser Welt sind. Doch die Substitutionen V, W und G entziehen sich jeglicher Vorstellungskraft. Das hat mathematische Analysis so an sich. Außerdem hätte man für die ganze Berechnung fast genauso viele Logarithmen gebraucht wie zu dem Schritt für Schritt Verfahren über die Dreiecke. Außerdem ist nicht vorstellbar, wie diese vorstehende Gauß-Analyse einem Seefahrer oder heute einem Skipper in einer Segelschule vermittelt werden könnte. Derartig “leblose” Gleichungen kann nur ein Computer verarbeiten.
Die Gauß Methode ist in der nautischen Literatur auch international nicht überliefert. Heute werden Gauß oft das Bild mit den sich überlappenden Höhenkreisen und die direkte Berechnung eines Standortes über die drei sphärischen Dreiecke zugeschrieben. Beides ist jedoch viel älter und hat mit Gauß gar nichts zu tun.
Im Jahre 1949 veröffentlichte der damals recht populäre Mathematiker Heinrich Dörrie in seinem Buch Ebene und sphärische Trigonometrie unter dem Titel „Gauß’ Zweihöhenproblem.“ einen Aufsatz, in dem er die Breite anhand des geometrischen Modells mit verschiedenen Formeln aus der spärischen Geometrie präsentierte. Dazu benutzte er nacheinander die Neperschen Formeln, den Sinussatz, den Tangenssatz für den Halbwinkel und schließlich den Kosinus Seitensatz. Genau diesen Lösungsweg wollte Gauß ja geade vermeiden, was er klar in seiner Einleitung zu den Berechnungen formulierte, nachdem er das geometrische Modell verbal beschrieben hatte:
„Dieses alles beruhet auf rein geometrischen, freilich ganz einfachen Betrachtungen: es wird aber ohne Zweifel manchem angenehm seyn, eine directe Auflösung dieses Problems auf blos analytischem Wege entwickelt zu sehen wodurch sich aufs Neue bestätigen wird, daß alle Wahrheiten, welche aus geometrischen Betrachtungen abgeleitet werden, ebenso zierlich mit Hülfe der Analyse entdeckt werden können, wenn diese nur auf die rechte Art behandelt wird.“
Bemerkenswert ist, dass die Gauß Methode in dem in sehr vielen Auflagen über Jahrzehnte erschienenden Lehrbuch „Steuermannskunst“ von Arthur Breusing, dem bedeutendsten deutschen Navigationslehrer des 19. Jahrhunderts, nicht einmal erwähnt wird. Dabei hat Breusing sogar in Göttingen Astronomie studiert. Das ist höchst verwunderlich, denn Breusing gab analytischen Navigationsverfahren den Vorzug. Er lehnte sogar das Sumner Prinzip ab, weil es eine grafische Grundlage hatte und nahm die ebenfalls grafische Methode von Hilaire erst in einer recht späten Auflage seines Buches auf, aber nur, weil sie international schon sehr verbreitet war. Dabei ist gerade die Gauß Methode das brillianteste analytische Stück der Lösung des Zweihöhenproblems überhaupt.
Heute, im Zeitalter des Computers, stehen analytische Lösungen auf allen Gebieten absolut im Vordergrund und dabei wäre die Methode von Gauß ohne Frage der Algorithmus der Wahl, wenn es um die Digitalisierung der astronomischen Navigation für Hobby oder Backup Anwendungen geht. Doch leider ist die Gauß Methode nur in der Originalversion von 1809 oder als Faximile zu bekommen und ist seitdem nie wieder aufgetaucht.
Logarithmische Berechnung
An einem Beispiel soll nun gezeigt werden, wie eine logarithmische Berechnung eines Standortes nach der Gauß Methode ausgeführt wird. Das soll aufzeigen, wie die Seeleute damals die Gauß-Methode bei zwei Beobachtungen ohne Versegelung hätten anwenden müssen.
Aus diesen Daten werden nun die Positionen der Sonne bzw. ihres Bildpunktes berechnet, was mit Hilfe eines Nautischen Jahrbuches möglich ist, hier jedoch mit den Formeln aus dem Kapitel „ die Sonne am Himmel“ erfolgt:
Außerdem wird der Stundenwinkel der Sonne zwischen beiden Beobachtungen gebraucht, der sich aus dem Produkt der verstrichenen Zeit und der Winkelgeschwindigkeit der Sonne von 15°/h oder einfach aus der Differenz der Greenwichwinkel ergibt:
![]() = Grt’ – Grt = 38,1224°
= Grt’ – Grt = 38,1224°
Gauß war der Ansicht, dass eine Standortberechnung nach seiner Methode ganz einfach sei. In der Tat fallen lediglich Additionen und Subtraktionen an. Die Arbeit mit Logarithmentafeln ist jedoch ganz erheblich, denn für einen unversegelten Standort müssen schon 21 Logarithmen aufgesucht und für 7 Logarithmen die reellen Zahlen gefunden werden, wobei jedesmal auch noch eine kleine Interpolationsrechnung fällig ist. Die Berechnung der Breite des unversegelten Standortes, wenn sich also der Standort zwischen den Beobachtungen nicht geändert hätte, würde dann folgendermaßen ablaufen:
Die Ergebnisse des Stundenwinkels ![]() und der Breite
und der Breite ![]() liegen ursprünglich als Radiant vor. Eine Multiplikation mit 180/
liegen ursprünglich als Radiant vor. Eine Multiplikation mit 180/![]() führt auf das Ergebnis in Grad. Wie oben schon gezeigt, ist die Standortlänge die Summe aus Grt und
führt auf das Ergebnis in Grad. Wie oben schon gezeigt, ist die Standortlänge die Summe aus Grt und ![]() , also 32,74° + 320,72° = 353,43°. Das ist immer noch ein Stundenwinkel, der auf geografische Ost- bzw. Westgrade anzupassen ist. Wenn die erhaltene Summe kleiner als 180° wäre, dann würde es sich um Westgrade handeln. Werte von großer als 180° sind von 360° abzuziehen und das Ergebnis sind Ostgrade. Das muss hier gemacht werden und man rechnet 360° – 353,43° = 6,55°. Damit lautet der Standort:
, also 32,74° + 320,72° = 353,43°. Das ist immer noch ein Stundenwinkel, der auf geografische Ost- bzw. Westgrade anzupassen ist. Wenn die erhaltene Summe kleiner als 180° wäre, dann würde es sich um Westgrade handeln. Werte von großer als 180° sind von 360° abzuziehen und das Ergebnis sind Ostgrade. Das muss hier gemacht werden und man rechnet 360° – 353,43° = 6,55°. Damit lautet der Standort:
41° 41,24′ N / 006° 32,81′ E
In dieser Berechnung wird 28 mal auf eine Logarithmentafel zugegriffen. Das ist im Vergleich mit der Methode der Breitenberechnung über die Dreiecke mit anschließender Chronometer-Längenberechnung, wo insgesamt 32 Tafelzugriffe nötig sind, kein allzu großer Fortschritt. Der klare Vorteil bei Gauß ist die Kompaktheit seines Formelsystems. Zur Berechnung des möglichen südlichen Standortes ist nichts weiter nötig, als W ein negatives Vorzeichen zu geben. Leider ist die Gauß Methode nicht vermittelbar. Während bei der Methode über die Dreiecke jeder Rechenschritt auf ein real vorhandenes Element führt, besteht das Ergebnis der Gauß Methode im Grunde nur aus abstrakten mathematischen Schritten, die sich an keiner modellhaften Vorstellung orientieren. Deshalb kann ein Standort nach Gauß nur berechnet werden, ohne dass der Rechenweg den Seeleuten in der Praxis plausibel erscheinen könnte. Mit derartigen Voraussetzungen können nur Computer gut arbeiten.
Gauß heute
Die Gauß Methode ist nie in der Seefahrt verwendet worden und heute vergessen. Genau betrachtet ist es auch nur ein anderer, dafür aber ein sehr eleganter Lösungsweg der wesentlich älteren geometrischen Methode zur Berechnung der Breite über die drei Dreiecke. Die wurde auch in der neueren Literatur hin und wieder beschrieben und wird allgemein sogar als Gauß Methode bezeichnet. Gauß hat damit aber nichts zu tun. Vielleich beruht dieser Irrtum auf einem Beitrag in einem Buch über die Trigonometrie von Heinrich Dörrie, einem sehr bekannten und sogar populären Mathematiker aus der Mitte des 20. Jahrhunderts. Darin beschreibt er unter der Überschrift “Gauß und das Zweihöhenproblem” nicht die Gauß Methode, sondern die viel ältere geometrische Methode mit den drei Dreiecken.
Wenn beispielsweise die erste Beobachtung um 23:00 UT1 und die zweite um 1:00 UT1 erfolgte, dann rechnen die Gauß Formeln automatisch mit einer Zwischenzeit von 2 Stunden. Dem geometrischen Verfahren muss dagegen extra mitgeteilt werden, dass die zweite Beobachtung am Folgetag stattgefunden hat. Außerdem muss immer die Peilrichtung angegeben werden, ob die Sonne im Osten oder im Westen beobachtet wurde, was sich bei Gauß ebenfalls erübrigt.
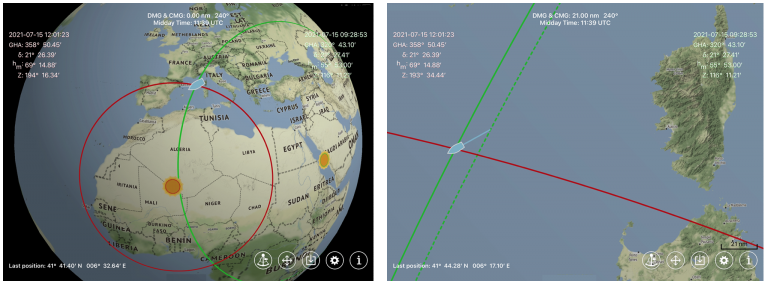
Unabhängig davon ermöglicht die Verfügbarkeit von Computern endlich eine Benutzung der alten und präzisen analytischen Methoden. Optimal funktioniert das nur mit einem Programm, in das dann auch gleich eine elektronische Karte integriert ist. Das gibt es bisher nur in der Satellitennavigation, ähnlich einfach geht das aber auch mit den Gauß Formeln oder dem Verfahren der Berechnung über die drei Dreiecke. Damit das endlich mal realisiert wird, habe ich die Gauß Methode in verschiedenen Navigationsprogrammen umgesetzt. Zuerst in einer Tabellenkalkulation, die später als Vorlage zur Programmierung einer App für mobile Anwendungen diente.
Die Vorteile sind ganz klar. Ein Hobbynavigator kann jetzt wie die alten Seefahrer mit einem Sextanten navigieren, ohne auf die lästigen Berechnungen angewiesen zu sein, was ihm bestimmt die Anerkennung seiner Mitsegler einbringt. Im Notfall wird jedermann ohne weiteres mit der App zurechtkommen, da sie selbsterklärend ist. Man muss ja nichts weiter tun, als die Sonnenhöhe und die Beobachtungszeiten von zwei Beobachtungen eintragen und bekommt seinen Standort auf der Karte im Display angezeigt und als Zahl ausgegeben.
Wer sich tiefergehend für die gesamten Berechnungsabläufe in der App interessiert, der findet diese im Beitrag Navigationsprogramm mit Excel selbst gemacht ausführlich dargelegt. In diesem kleinen Excel Sheet wird auch gezeigt, wie die Sonnenephemeriden, also die Deklination und der Greenwichwinkel der Sonne in diesem Jahrhundert aus ihren Bahnparametern berechnet werden. Dieselbe Berechnung ist in der App “Sun Navigation Basic” umgesetzt. In der Pro Version werden für die Ephemeriden Datenbanken verwendet.