Die Navigation mit der Sonne hatte schon immer die größte Bedeutung in der astronomischen Navigation. Mit Sternen kann nur in der Dämmerung oder am Tage navigiert werden. Nachts ist eine Navigation mit Sternen nicht möglich, weil zu deren Höhenmessung mit dem Sextanten auch der Horizont sichtbar sein muss. Mondlicht macht in der Nacht zwar eine Horizontlinie sichtbar, die ist jedoch eine optische Täuschung. Der wahre Horizont liegt viel tiefer. Mond und Sterne können als Navigationsgestirne nur am Tag gut verwendet werden, wenn sie überhaupt sichtbar sind. Eine Navigation mit Sternen in den kurzen Zeiten der Dämmerung hat den Vorteil, dass man einen Standort sofort erhält, ohne Versegelungen berücksichtigen zu müssen. Ein weiterer Vorteil besteht darin, dass man sich etwas höher stehende Sterne aussuchen kann, wodurch der Einfluss der Lichtbrechung nicht ganz so groß ist. Wer mit Sternen navigieren will, muss sich jedoch sehr gut am Sternenhimmel zurechtfinden, damit keine Verwechslungen auftreten.
Letztendlich liegt die Bedeutung der Astronavigation heute neben einer Notfallnavigation nur noch in der Ausübung als Hobby. Man will auf einem Segelschiff genauso navigieren können, wie die alten Seefahrer es einst taten. Für diese Zwecke ist eine Navigation mit der Sonne allgemein ausreichend genug. Auch in früheren Zeiten haben die Seeleute am liebsten und am häufigsten am Tag mit der Sonne navigiert.
1 Bildpunkt und Höhengleiche
In der terrestrischen Navigation verwenden wir zur Orientierung die in den Seekarten eingezeichneten bekannten Positionen von Türmen, Gebäuden oder Bergen. Auf hoher See stehen uns diese nicht zur Verfügung. Dafür haben wir dort die Sterne und tagsüber die Sonne. Die Positionen der Gestirne sind jedoch nicht fest und was ist überhaupt die Position eines Gestirns? Die Gestirne stehen am Himmel und sind praktisch unendlich weit entfernt. Wie sollen da ihre Positionen auf der Erde angegeben werden können, wie z. B. die Position eines Leuchtturms? Wie bekommt man also eine Position der Sonne auf die Erdoberfläche?
Die Lösung ist der Bildpunkt. Das ist der Punkt, an dem eine gerade Linie zwischen dem Erdmittelpunkt und dem Mittelpunkt eines Gestirns, in unserem Fall der Sonne, die Erdoberfläche durchbricht. Es ist genau der Ort, an dem die Sonne gerade im Zenit steht.

Erschwerend ist jedoch, dass dieser Punkt infolge der Erdrotation mit Überschallgeschwindigkeit von Ost nach West rast. Terrestrische Orientierungspunkte bleiben dagegen immer am selben Ort. Eine zusätzliche und ganz wichtige Bedeutung bei der astronomischen Navigation hat deshalb die Zeit. Die Position eines Bildpunktes gilt nämlich nur für einen Augenblick, praktisch nur für eine Sekunde.
Ein Navigator beobachtet die Sonne selten im Zenit, sondern sieht sie vielmehr in einer bestimmten Höhe h über dem Horizont. Dieser Horizontabstand wird im Winkelmaß gemessen und beträgt 0° bei Sonnenaufgang und würde 90° sein, wenn die Sonne tatsächlich im Zenit eines Beobachters stehen würde.
Eine bestimmte Höhe der Sonne über dem Horizont kann in derselben Sekunde von allen Beobachtern festgestellt werden, die vom Bildpunkt denselben Abstand haben und sich so z. B. auf der im Bild 1 dargestellten grünen Linie befinden. Diese Linie hat deshalb den bezeichnenden Namen Höhengleiche. Im englischen wird sie Circle of Position (Positionskreis) genannt. Mit dem Positionskreis ist die Position eines Schiffes durch Bestimmung des Horizontabstandes h schon mal definiert, nämlich genau irgendwo auf dieser Kreislinie. Auf einem Globus und damit auf der Erdoberfläche ist diese Linie kreisrund mit dem Bildpunkt als Mittelpunkt.
Wir stellen uns jetzt mal vor, wir wären in Sizilien und sehen die Sonne am Nachmittag bereits im Westen. Ihr Bildpunkt befindet sich, wie im Bild 1 gezeigt, schon im Atlantik. Die Sonne wandert weiter nach Westen, ihr Bildpunkt entfernt sich von uns und ihre sichtbare Höhe h nimmt ab. Wir können uns leicht ausmalen, dass der grüne Positionskreis dadurch immer größer wird. Bald geht er sogar über den Nordpol hinweg. Größer als der Erddurchmesser kann er jedoch nicht werden und das ist dann der Punkt, wo die Sonne, wenn man den Lichtbrechungsfehler außer acht lässt, zur Hälfte im Meer versunken ist.
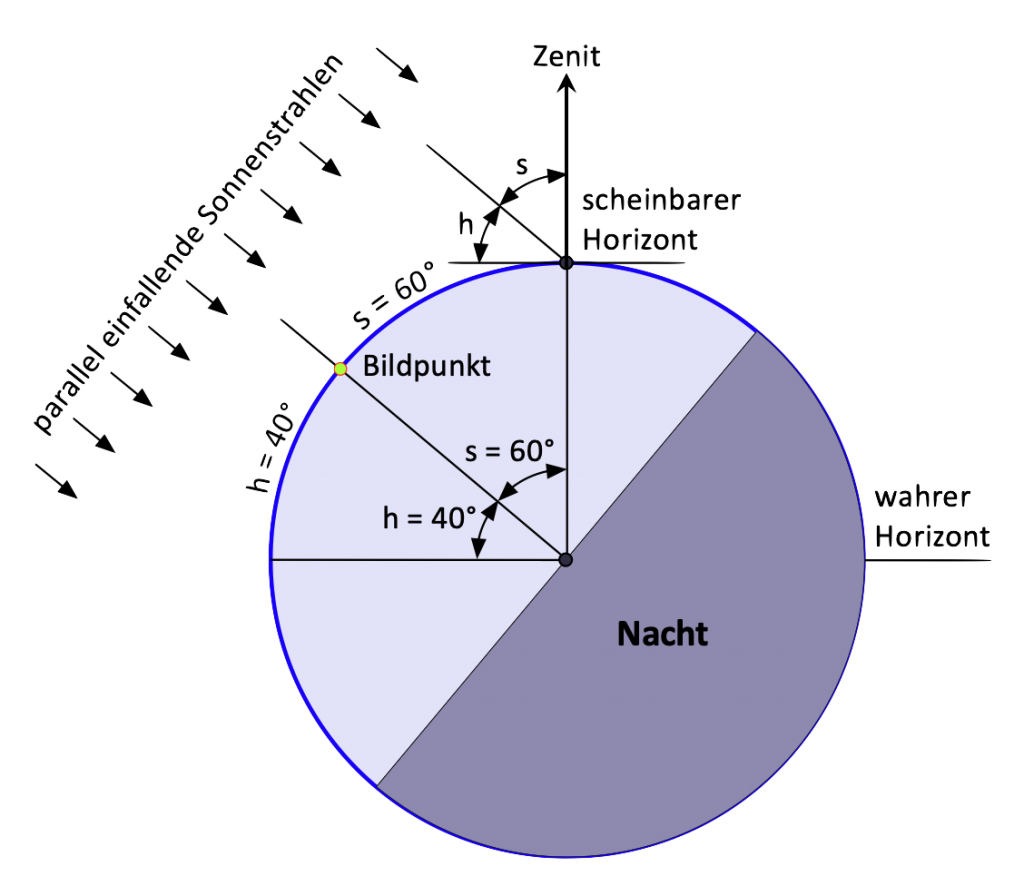
Daraus leiten wir als Erkenntnis ab, dass die sphärische Distanz zwischen der Position eines Beobachters und dem Bildpunkt der Sonne aus dem beobachteten Horizontabstand berechnet werden kann. Unter sphärischer Distanz wird die Distanz entlang der Erdkrümmung verstanden. Die Zusammenhänge werden im Bild 2 deutlich. Von seinem scheinbaren Horizont aus stellt ein Beobachter beispielsweise einen Horizontabstand h im Winkel von 40° fest. Weil der Zenit des Beobachters immer 90° beträgt, ergibt sich damit gleichzeitig ein Zenitabstand von 90° – 40° und somit s = 60°.
Nehmen wir jetzt an, dass die Sonne sinkt und dabei die Höhe h bis auf null abnimmt, dann fallen die Sonnenstrahlen bei Sonnenuntergang im scheinbaren Horizont des Beobachters waagerecht ein. Das ist dann der Moment, in dem die Distanz zwischen Beobachter und Bildpunkt der Sonne genau ein Viertel des Erdumfangs und der Horizontabstand s = 90° betragen.
Bei einem Erdumfang von 40 000 km oder 21 600 Seemeilen (NM) beläuft sich ein Viertel des Erdumfangs auf genau 5 400 NM. Besser ist es jedoch, gleich mit Winkelmaßen zu rechnen. Bei einem Erdumfang von 360° sind ein Viertel dann 90°. Ein Grad entspricht hier auf einem Großkreis einer Distanz von 60 NM. Da auch der Horizontabstand im Gradmaß gemessen wird, etwas anderes wäre gar nicht möglich, ergibt sich sofort ein direkter Zusammenhang:
Der von einem Beobachter festgestellte Zenitabstand der Sonne ist identisch mit der Distanz zwischen dem Beobachter und dem Bildpunkt der Sonne.
Da der Himmel im Zenit keine Markierung besitzt, muss zur Bestimmung des Zenitabstandes der Horizontabstand von 90° subtrahiert werden. Damit ist der Zenitabstand das Komplement des Horizontabstandes und umgekehrt. Eine Multiplikation des in Grad vorliegenden Ergebnisses mit 60 NM/ Grad liefert die Distanz des Beobachters zum Bildpunkt schließlich in Seemeilen.
2 Das Nautische Jahrbuch
Allein aus der Höhe der Sonne kann nur der sphärische Radius des Höhenkreises genau bestimmt werden. Die genaue Lage des dadurch auf dem Globus vorstellbaren Kreises wird jedoch von der Position des Kreismittelpunktes, des Bildpunktes der Sonne, bestimmt und ist zeitabhängig. Vollständige Zeitangaben umfassen das Datum und die Tageszeit und so muss die Zeitabhängigkeit über ein ganzes Jahr betrachtet werden. Über ein Jahr gesehen schwankt die Abweichung des Kreismittelpunktes zwischen 23,44° Nord und 23,44° Süd. Anstelle des früher verwendeten Begriffs Abweichung (vom Äquator) wird heute der Begriff Deklination verwendet. Das Formelzeichen dafür lautet ![]() .
.
Sehr viel dynamischer wird die Position des Bildpunktes der Sonne und überhaupt aller Gestirne von der Rotation der Erde um sich selbst bestimmt. Dafür ist dann die Tageszeit verantwortlich, denn der Bildpunkt umkreist die Erde einmal in 24 Stunden und gesucht wird jeweils der Meridian, auf dem sich der Bildpunkt in jeder Sekunde eines Tages gerade befindet. Für diese Angabe verwendet man aber nicht einfach die geografische Länge, sondern benutzt aus Gründen der Kontuität den Stundenwinkel. Dieser wird mit GHA (Greenwich Hour Angle) bezeichnet und läuft vom Nullmeridian ausgehend in 360° einmal um die Erde. Als Nullmeridian wurde der durch die Sternwarte im Londoner Stadtteil Greenwich verlaufende Meridian festgelegt. Im deutschen Sprachgebrauch wird dieser Stundenwinkel mit Greenwichwinkel oder kurz mit Grt bezeichnet.
Die Position des Bildpunktes der Sonne und überhaupt aller Gestirne, wird also mit den Daten von Deklination und Greenwichwinkel beschrieben. Diese Positonsdaten werden auch als Ephemeriden bezeichnet. Um Deklination ![]() und Greenwichwinkel der Sonne für jede Sekunde eines Jahres tabellarisch zu erfassen, reicht eine kleine Tabelle nicht aus, das hat schon den Umfang eines Buches, des sogenannten nautischen Jahrbuches oder nautischen Almanaches. In diesen Tabellenbüchern wurden dann auch gleich die Ephemeriden aller zur Navigation tauglichen Gestirne erfasst, also von Sonne, Mond, Planeten und Fixsternen. Auf 365 Tagesseiten dieses Buches befanden sich die Werte von Deklination und Greenwichwinkel im Stundenraster zehntel Minuten genau berechnet. Am Ende des Buches gab es die sog. Schalttafeln zur Berechnung des Minuten- und Sekundenwertes in der jeweils angebrochenen Stunde. Der damit gefundene Zuwachs für Grt bzw. der VB-Wert für δ wird zum jeweiligen Stundenwert addiert. Das Ergebnis ist die sekundengenaue Position des Bildpunktes und die minutengenaue Deklination zum gegebenen Zeitpunkt.
und Greenwichwinkel der Sonne für jede Sekunde eines Jahres tabellarisch zu erfassen, reicht eine kleine Tabelle nicht aus, das hat schon den Umfang eines Buches, des sogenannten nautischen Jahrbuches oder nautischen Almanaches. In diesen Tabellenbüchern wurden dann auch gleich die Ephemeriden aller zur Navigation tauglichen Gestirne erfasst, also von Sonne, Mond, Planeten und Fixsternen. Auf 365 Tagesseiten dieses Buches befanden sich die Werte von Deklination und Greenwichwinkel im Stundenraster zehntel Minuten genau berechnet. Am Ende des Buches gab es die sog. Schalttafeln zur Berechnung des Minuten- und Sekundenwertes in der jeweils angebrochenen Stunde. Der damit gefundene Zuwachs für Grt bzw. der VB-Wert für δ wird zum jeweiligen Stundenwert addiert. Das Ergebnis ist die sekundengenaue Position des Bildpunktes und die minutengenaue Deklination zum gegebenen Zeitpunkt.
Nautische Jahrbücher kamen etwa in der Mitte des 20. Jahrhunderts in Mode. Das BSH hat den Druck und den Vertrieb des Nautischen Jahrbuchs im Jahr 2020 eingestellt, weil dieses Buch für die Großschiffahrt nicht mehr ausrüstungspflichtig ist. Es wird inzwischen als ausreichend angesehen, wenn die Großschifffahrt über zwei völlig unabhängige automatische Satelliten-Navigationseinrichtungen mit elektronischen Karten verfügt, die mit den drei Satellitensystemen GPS, Galileo und GLONASS kommunizieren können. Derartig abgesicherte Anlagen stehen kleineren Wasserfahrzeugen und der Sportschifffahrt natürlich nicht zur Verfügung.
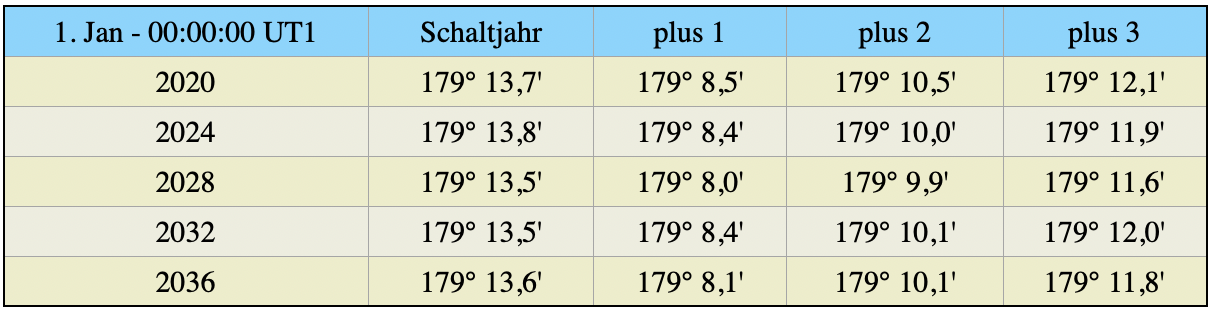
Die Positionen in jeder Sekunde eines Jahres sind nicht gleich mit denen derselben Sekunde des nächsten Jahres. Das liegt schon daran, dass unser Kalender nicht genau auf ein Jahr passt und wir deshalb sogar gezwungen sind alle vier Jahre einen Schalttag einzubauen. Doch auch alle vier Jahre sind die Positionen nicht gleich, wie die nachstehende Tabelle zeigt.
Die Werte in der Tabelle geben den Greenwichwinkel Grt um 00:00:00 UT1 an. Der Ort liegt an der Datumsgrenze in der Nähe der Fidschi Inseln. Die Schwankungen betragen etwa 0,5′, was 0,5 nm entspricht. Für den Notfall könnte man also im Abstand von jeweils vier Jahren mit demselben NJ navigieren.
Mit Hilfe einer Tabellenkalkulation wie MS Excel oder Numbers, eines davon hat jeder auf seinem heimischen Computer, ist es kein Hexenwerk, sich den Greenwichwinkel und die Deklination für die Sonne selbst auszurechnen – und wer unbedingt noch grafisch unterwegs sein will, auch auszudrucken. Der folgende Link führt auf eine fertige Rechentabelle:
hundertjährige Ephemeriden 1.1
Dabei hadelt es sich um ein einfaches Programm, das nach dem Kepler Modell nur die Massen von Erde und Sonne berücksichtigt. Die Einflüsse der Massen von Mond und Planeten bleiben dagegen unberücksichtigt. Die Abweichungen gegenüber amtlich herausgegebenen Daten liegen meist zwischen 0′ und 0,2′. Der Grt kann auch mal 0,5′ daneben liegen, was allerdings selten vorkommt. Wie diese Berechnungen durchgeführt werden, wird im Beitrag Ephemeridenrechnung gezeigt.
Abweichungen von einer halben Seemeile als Bildpunktfehler spielen in der praktischen Navigation nur eine untergeordnete Rolle. Gerade auf schwankenden Segelbooten muss man froh sein, eine Standortabweichung von weniger als 2 Seemeilen erreichen zu können und da sind Abweichungen von 0,5′ in der Angabe des Grt fast ohne Bedeutung. Nach dem Fehlerfortpflanzungsgesetz addieren sich Einzelfehler nicht arithmetisch sondern geometrisch, d. h. ein Gesamtfehler ist die Wurzel aus den Quadraten der Einzelfehler. Dazu ein Beispiel:
Auf eine Positionsabweichung werden folgende Einflüsse angenommen:
- Seegang 2 NM
- Zeitmessung 1 NMm
- Rechenverfahren 0,5 NM
- Beschickungsfehler 1 NM
- Grafikfehler 0,5 NM
- Bildpunktfehler 0,5 NM
- ….
Die damit zu erwartende Positionsabweichung errechnet sich aus:
![]()
Wenn wir alle hier genannten Fehler, die ja positiv oder negativ sein können, in diese Formel eintragen, so errechnet sich daraus eine Positionsabweichung von 2,60 NM. Lassen wir den Bildpunktfehler weg, weil wir ein super genaues nautischen Jahrbuch verwenden, dann kommen wir auf einen Positionsabweichung von 2,55 NM. Das ist ein Unterschied von gerade mal 100 Metern, obwohl die Angabe der Bildpunktposition fast 1000 Meter daneben liegt. Eine Abweichung von 0,5’ bzw. NM in der Angabe der Position des Bildpunktes macht also kaum etwas aus, weil einfach noch viele andere stärker wirkende Fehlerarten im Spiel sind.
3 Die Zeitgleichung
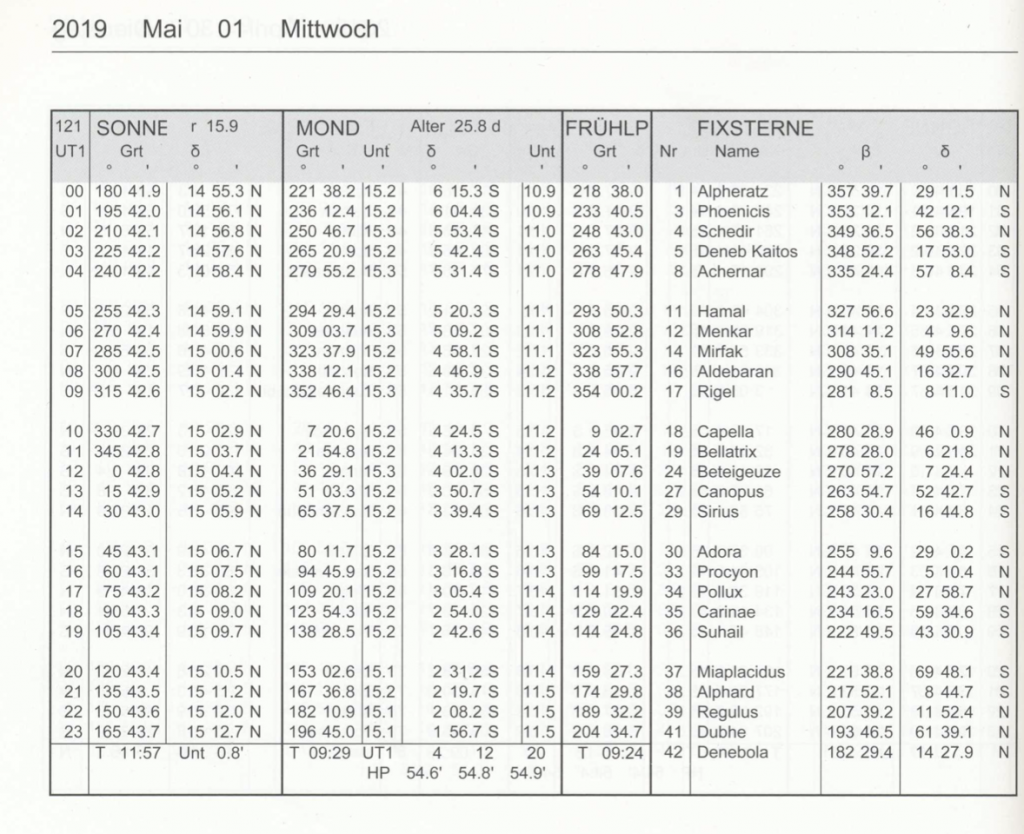
Die obige Abbildung der Seite des nautischen Jahrbuches vom 1. Mai 2019 gibt unterhalb der Grt-Spalte mit T 11:57 den Transitus an. Das ist die Universalzeit UT1, in welcher der Bildpunkt der Sonne den Nullmeridian passiert. Durch Blättern in einem Nautischen Jahrbuch stellt man dann auch schnell fest, dass die Sonne den Nullmeridian im Laufe eines Jahres zu ganz unterschiedlichen Zeiten zwischen etwa 15 Minuten vor oder nach 12:00 UT passiert und nur 4-mal im Jahr genau um 12:00 UT.
Die früher von einem Chronometer angegebene Zeit GMT (Greenwich Mean Time) oder die von der Erdrotation abgeleitete Zeit UT1 bzw. die von einer Atomuhr produzierte koordinierte Weltzeit UTC sind völlig gleichmäßig ablaufende Zeiten sogenannter Räderuhren. Sie unterscheiden sich von der natürlichen und von der Sonne vorgegebenen Sonnenzeit, die sich aus dem Umlauf der Erde um die Sonne ergibt durch die sogenannte Zeitgleichung. Die Zeitangaben der Räderuhren sind somit mittlere Zeiten. Eine Zeitgleichung ist keine mathematische Gleichung, sondern meist eine Tabelle mit Zahlen zum Ausgleich der mittlen Zeiten einer Räderuhr, um daraus die wahre Sonnenzeit zu erhalten. Für eine Navigation mit der Sonne ist schließlich nur die Sonnenzeit zu gebrauchen. Für das Zustandekommen der Zeitgleichung gibt es zwei Hauptursachen, die nachstehend diskutiert werden.
3.1 Elliptizität der Erdbahn
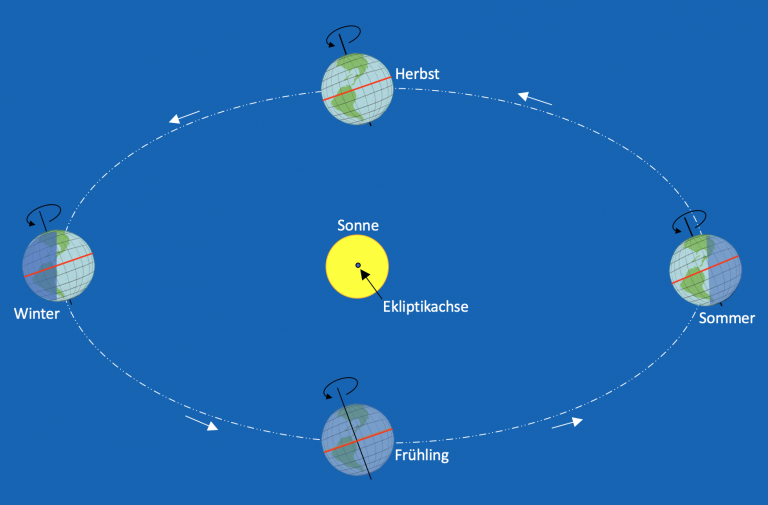
Gemäß dem ersten Keplerschen Gesetz umkreist die Erde die Sonne auf einer elliptischen Bahn, wobei sich die Sonne in einem Brennpunkt dieser Ellipse befindet. Die Form der Ellipse weicht nicht wesentlich von einem Kreis ab, denn ihre numerische Exzentrizität ist mit 0,0167 recht gering. In einer maßstabgerechten Zeichnung könnte man die tatsächliche elliptische Umlaufbahn optisch von einem Kreis gar nicht unterscheiden. Die Darstellung im Bild 3 ist deshalb stark übertrieben. Im Nordwinter kommt die Erde der Sonne am nächsten. Dann erscheint ihre Scheibe auch ein klein wenig größer. Im Sommer hat sie zur Sonne den größten Abstand. Der kleinste und der größte Abstand zur Sonne sind der Perihel und der Aphel und bilden die Enden der Hauptachse der Ellipse. Sie stimmen jedoch nicht exakt mit den Sonnenwenden überein. An den Sonnenwenden hat die Sonne ihre größte nördliche bzw. größte südliche Höhe über dem Horizont. Der Perihel wird gegenwärtig am 2. Januar erreicht, während die Sonne ihren niedrigsten Stand auf der Nordhalbkugel bereits am 21. Dezember, also einige Tage davor hat. Der Perihel ändert sich in 60 Jahren um etwa einen Tag.
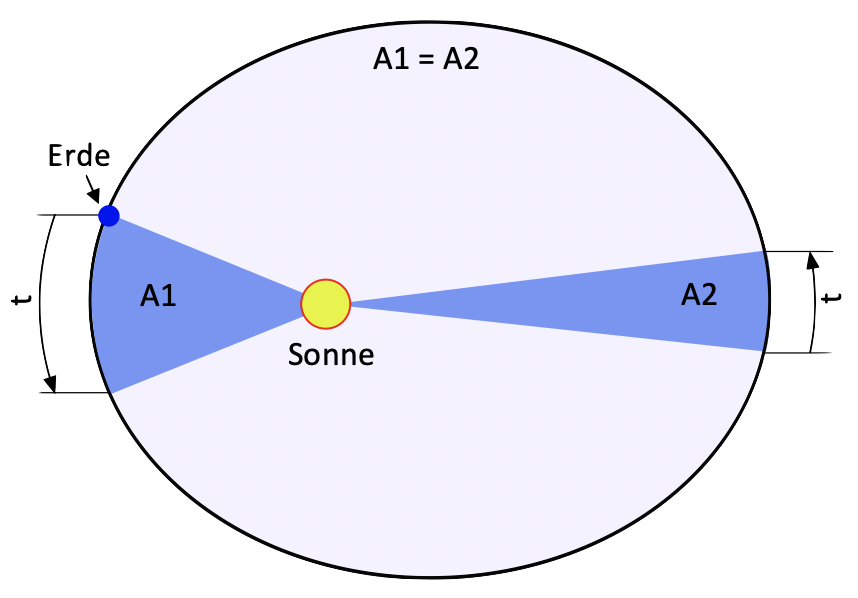
In Perihelnähe ist die Massenanziehung zwischen Erde und Sonne am größten. Damit die Erde dadurch nicht in die Sonne stürzt, erhöht sie zum Ausgleich der zunehmenden Gravitationskraft ihre Bahngeschwindigkeit und damit ihre Fliehkraft. Das hat Kepler in seinem zweiten Gesetz exakt beschrieben: „Ein von der Sonne zum Planeten gezogener Fahrstrahl überstreicht in gleichen Zeiten gleich große Flächen.“
Bild 3 zeigt das schematisch. Die Flächen A1 und A2 sind gleich groß und werden von einem Fahrstrahl zwischen Erde und Sonne in einem gleich großen Zeitintervall t überstrichen. Die Bahngeschwindigkeit der Erde ist bei dieser Betrachtung dann am größten, wenn in der Zeit t eine längere Strecke zurückgelegt wird.
Diese unterschiedlichen Geschwindigkeiten wirken sich auf die Zeitgleichung aus. Die Erde dreht sich sehr gleichmäßig und eine Drehung der Erde von 360° um sich selbst dauert 23 Stunden, 56 Minuten und 4,0905 Sekunden. Diese Zeit ist ein Sterntag, weil sich auf einem Meridian nach jeweils einem Sterntag immer wieder derselbe Sternenhimmel ausbreitet. Während sich die Erde dreht, kommt sie auf ihrer Bahn um die Sonne gleichzeitig ein Stück weiter. Bild 4 zeigt die Erde in der Position 1, wo die Sonne auf einem ihr gerade zugewandten Meridian kulminiert. Nach mehreren vollen Erdumdrehungen von jeweils 360° befindet sich die Erde in Position 2 und derselbe Meridian, der in Position 1 noch auf die Mitte der Sonnenscheibe zeigte, zeigt nun an der Sonne vorbei auf die Himmelskugel mit den Fixsternen. Damit derselbe Meridian an einem jeweils folgenden Tag wieder genau auf die Mitte der Sonnenscheibe zeigt, muss sich die Erde täglich etwa 4 min weiterdrehen und somit kommen wir auf 24 Stunden, die ein Sonnentag dauert.
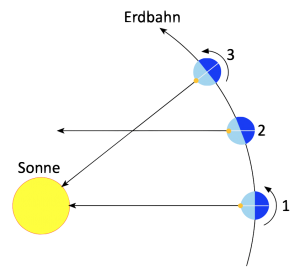
Wenn täglich immer nur genau 4 Minuten zum Sterntag addiert werden, damit die Sonne auf demselben Meridian kulminiert, erklärt das noch keinen Zeitunterschied zwischen Räderuhr und Sonnenzeit. Das wäre bei einer exakt kreisförmigen Erdumlaufbahn der Fall. Deshalb muss man sich am Bild 3 orientieren. In Sonnennähe bewegt sich die Erde auf ihrer Bahn schneller und das bedeutet, sie kommt innerhalb einer Tagesetappe ein Stück weiter voran, als in Sonnenferne. Die Erde läßt die Sonne auf ihrer Bahn jeden Tag ein Stück weiter zurück und muss dann auch jeden Tag etwas länger als 4 Minuten nachdrehen. In Richtung Nordsommer entfernt sich die Erde wieder von der Sonne und ihre Bahngeschwindigkeit nimmt ab. Sie legt jetzt auf ihrer Bahn in jeder Tagesetappe kleinere Stücke zurück und lässt die Sonne nicht mehr so weit zurück, wodurch sie auch nicht mehr so viel nachdrehen muss. Die Nachdrehzeiten sind dann kleiner als 4 Minuten.
Die daraus resultierende Änderung der wahren Tageslänge zwischen zwei aufeinanderfolgenden Tagen beträgt maximal etwa ±8 Sekunden. Da die sich summieren, ergibt sich innerhalb eines Jahres eine maximale Schwankung der wahren Sonnenzeit um etwa ±7,5 Minuten in einem angenähert sinusförmigem Verlauf.
3.2 Schiefe der Ekliptik
Eine zweite Ursache des Unterschiedes von Sonnenzeit und Chronometerzeit ist die Schiefe der Ekliptik. Die Erdachse steht etwa 23,44° schräg zur Ebene der Ekliptik und damit auch zur Achse der Ekliptik und diese Stellung ist in Bezug zum Fixsternhimmel nahezu unveränderlich. Von der Sonne aus gesehen scheint die Erdachse jedoch zu taumeln. An den Tag-und-Nacht-Gleichen steht sie von der Sonne aus gesehen einmal mit +23,44° und einmal mit -23,44° maximal schräg zur Ekliptikachse. In den Sonnenwenden steht sie zwar immer noch schräg zur Ekliptikebene, doch von der Sonne aus gesehen sind beide Achsen deckungsgleich. Dafür ist die Nordhalbkugel oder die Südhalbkugel der Erde der Sonne zugeneigt und werden jeweils direkter angestrahlt, woraus sich die Jahreszeiten ergeben. Um den Einfluss der Schiefe der Ekliptik auf die Zeitgleichung zu erfassen, müssen mindestens die folgenden drei Bewegungen berücksichtigt werden:
- Erdrotation 0,25°/min oder 15,00 NM/min am Äquator
- Bahngeschwindigkeit
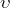 0,986°/d oder 59,14 NM/d Bildpunktspur auf der Erde
0,986°/d oder 59,14 NM/d Bildpunktspur auf der Erde - Deklination
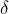
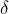 = 0° bis 23,44° vom 20. März bis 21. Juni
= 0° bis 23,44° vom 20. März bis 21. Juni
An dieser Stelle soll noch mal an den Bildpunkt oder Zenitalpunkt eines Gestirns erinnert werden. Der Bildpunkt der Sonne ist der Ort, an dem eine gedachte Linie zwischen dem Mittelpunkt der Sonne und dem Mittelpunkt der Erde die Erdoberfläche durchbricht. Es ist der Ort, an dem ein Beobachter die Sonne im Zenit sieht.
Die Erde ist nach jeder Umdrehung um sich selbst, eine Tagesetappe weitergekommen und muss deshalb im Mittel etwa 4 Minuten nachdrehen, damit die Sonne auf demselben Meridian des Vortages kulminiert. Dieser Kulminationsmeridian (im Bild 6 grün dargestellt) befindet sich nach jeder Drehung der Erde um sich selbst und vor Beginn der Nachdrehung westlich vom Bildpunkt. Die Länge dieses Nachdrehstücks lässt sich ausrechnen. Aus dem Produkt der Bahngeschwindigkeit von 0,986°/d und dem erdspezifischen Längenmaß von 60 NM/Grad erhält man
![]()
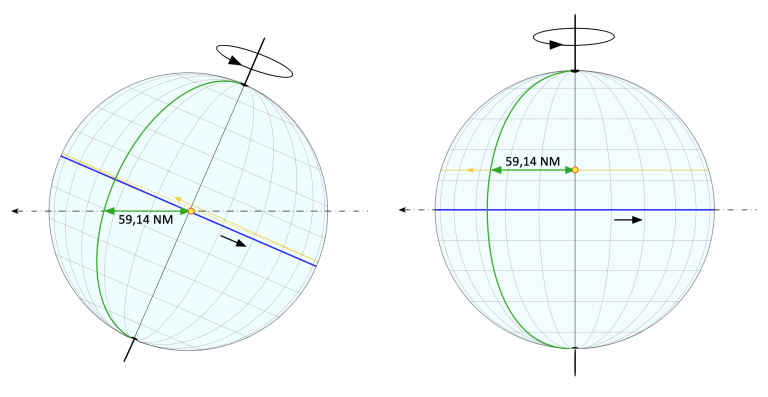
Diese Strecke liegt in der Ebene der Ekliptik bzw. senkrecht zur Achse der Ekliptik. Daraus lassen sich jetzt zwei Extreme ableiten, die im Bild 6 gezeigt werden. An den Tagundnachtgleichen, links im Bild, trifft der Bildpunkt der Sonne den Äquator. Infolge der Erdrotation zeichnet der Bildpunkt eine Linie, die längs des Äquators beginnt. Mit zunehmendem Weg auf der Umlaufbahn neigt sich eine der Erdhalbkugeln der Sonne zu. Damit weicht der Bildpunkt, wenn es dem Sommer zugeht, nach Norden aus und hinterläßt auf der Erdoberfläche infolge der Erdrotation eine Spiralbahn, mit immer enger zusammenliegenden Windungen. Beim Erreichen der Sommersonnenwende wird eine Bahn entlang des Wendekreises gezeichnet. Von der Sonne aus gesehen, scheint sich in diesem viertel Jahr die Erdachse völlig aufgerichtet zu haben.
Im Bild 6 links bilden der Kulminationsmeridian, der Äquator und die Tagesetappe von 59,14 NM bzw. s = 0,986° Großkreislänge ein rechtwinkliges Kugeldreieck, wobei der rechte Winkel natürlich zwischen Meridian und Äquator existiert. Dabei ist s die Hypotenuse und somit die längste Seite in diesem Dreieck. Wird dem Äquatorabschnitt der Wert ![]() zugewiesen und dem Winkel zwischen der Hypotenuse und dem Äquator der Wert
zugewiesen und dem Winkel zwischen der Hypotenuse und dem Äquator der Wert ![]() , dann gilt für dieses Dreieck:
, dann gilt für dieses Dreieck:
![]()
Nach Einsetzen der Zahlen s = 0,986° und ![]() = 23,44° errechnet sich daraus ein Winkel
= 23,44° errechnet sich daraus ein Winkel ![]() von 0,904°. Mit ihrer Rotationsgeschwindigkeit von 15°/h muss die Erde dafür genau 3,618 Minuten nachdrehen bis der grün gezeichnete Meridian im Bildpunkt angekommt. Die Differenz zu der mittleren täglichen Nachdrehzeit von 3,943 Minuten beträgt hier -19,51 Sekunden. Damit ist ein Sonnentag am Frühlingsanfang und ebenso am Herbstanfang kürzer ist als ein mittlerer Sonnentag.
von 0,904°. Mit ihrer Rotationsgeschwindigkeit von 15°/h muss die Erde dafür genau 3,618 Minuten nachdrehen bis der grün gezeichnete Meridian im Bildpunkt angekommt. Die Differenz zu der mittleren täglichen Nachdrehzeit von 3,943 Minuten beträgt hier -19,51 Sekunden. Damit ist ein Sonnentag am Frühlingsanfang und ebenso am Herbstanfang kürzer ist als ein mittlerer Sonnentag.
In den Wendepunkten ist die Nord- oder Südhalbkugel der Sonne zugeneigt und der Bildpunkt der Sonne schreibt seine Spur mit der Erdrotation auf einem Wendekreis. Dort liegen die Meridiane dichter zusammen und der Winkel ![]() , den der Vortagsmeridian für die Nachdrehung bis zur Kulmination noch braucht ist um den Drehwinkel
, den der Vortagsmeridian für die Nachdrehung bis zur Kulmination noch braucht ist um den Drehwinkel
![]()
vom Bildpunkt entfernt. Das sind 1,075°, wozu die Erde dann 4,299 Minuten nachdrehen muss muss. Das sind dann 21,32 s mehr als die mittlere Rotationszeit und damit ist der Sonnentag an den Sonnenwenden um diese Zeit länger als die mittlere Sonnenzeit.
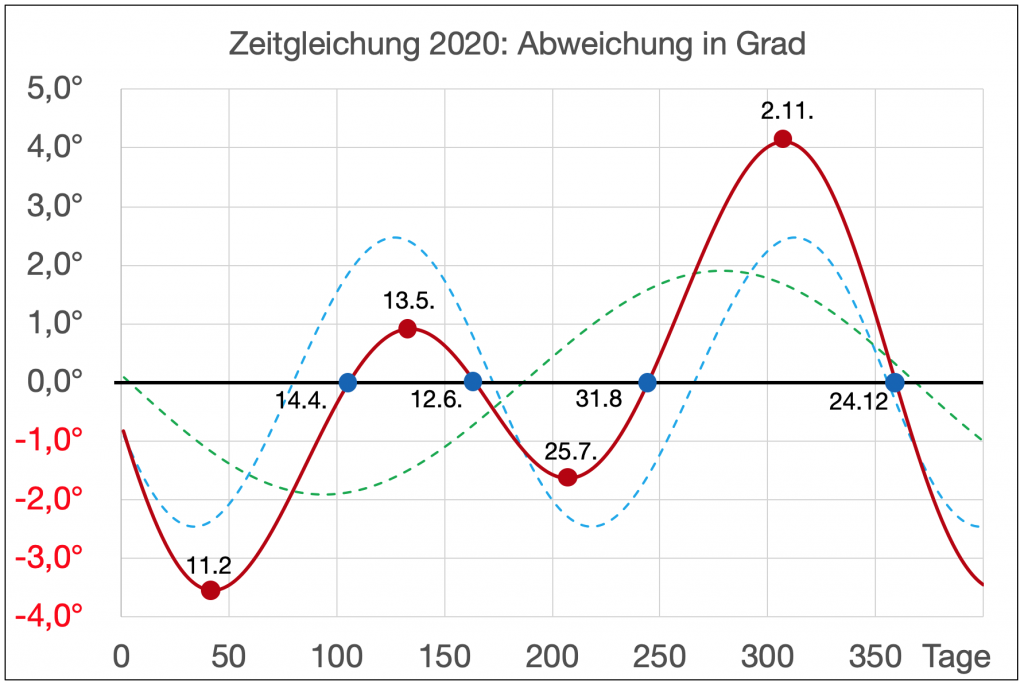
Vom Frühlingsanfang beginnend addieren sich die täglichen Sekunden etwa 46 Tage lang bis auf etwa 9,85 Minuten. Diese Summe nimmt dann in den weiteren 46 Tagen bis zur Sommersonnenwende wieder bis auf 0 ab. Weil das viermal im Jahr geschieht ergeben sich über das ganze Jahr gesehen zwei komplette sinusähnliche Wellen. Der Unterschied zu einer reinen Sinuswelle besteht darin, dass die Steilheit in den Nulldurchgängen etwas größer ist.
3.3 Summierung der Effekte
Die beiden beschriebenen Effekte haben vollig unabhängige Ursachen und können deshalb einfach addiert werden. Da der Kalender nicht genau auf ein Jahr passt und deshalb von Zeit zu Zeit mit Schalttagen der Umlaufbahn der Erde angepasst werden muss, sind die Daten der Maxima und Minima, die in den Kurven angegeben werden in jedem Jahr etwas verschieden. Hinzu kommt, dass sich auch die Elliptizität der Erdbahn und die Lage der geneigten Erdachse im Laufe der Zeit ändern. Das macht es nicht gerade einfach, wenn ein nautisches Jahrbuch erstellt werden soll. Zwar beginnt jedes neue Jahr mit dem 1. Januar 00:00 Uhr, doch der Bildpunkt der Sonne befindet sich nie auf derselben Position wie zu Beginn des Vorjahres.
Das Problem ist, dass die Erde auf exakt einer Umlaufbahn um die Sonne keine ganzzahlige Anzahl von Umdrehungen um sich selbst vollführt. Da bleibt immer ungefähr ein viertel Tag übrig. Wenn es wenigstens genau ein viertel Tag wäre, dann könnte man mit den Schalttagen zurecht kommen. Es sind dann aber noch etwa 11 Minuten übrig. So unterscheidet sich der Beginn eines jeden Jahres vom Beginn des nächsten. Wann ein Jahr beginnt, ist mit einem Tageskalender nicht in Einklang zu bringen und wird deshalb vom julianischen Kalender aus dem Jahr 45 v. Chr. abgeleitet. Der Name geht auf Julius Cäsar zurück. Im Jahre 1582 wurde der julianische Kalender von Papst Gregor reformiert. Zunächst um 10 Tage und eine etwas andere Schaltjahresregel weil die 11 Minuten im Laufe der Jahrhunderte den Frühlingsanfang auf den 11. März verschoben hatten. Heute beträgt die Differenz der Tage zum julianischen Kalender aufgrund der neuen Schaltregel 13 Tage.
Die Berechnung des Bildpunktes der Sonne jeweils ab dem 1. Januar 00:00 Uhr eines jeden neuen Jahres ist eine Fortschreibung aller Jahre vom Beginn des julianischen Kalenders an. So ist auch der Beginn der jährlichen Zeitgleichung nicht auf den 1. Januar des aktuellen bzw. angegebenen Jahres bezogen, sondern ebenfalls eine Fortschreibung sämtlicher Jahre vom Beginn des julianischen Kalenders an.
Die Wirkung der Zeitgleichung wurde den Menschen erst bewusst, als es gleichmäßig gehende Uhren gab. Die wichen mit Ihrer Zeit von den Zeiten der bis dahin üblichen Sonnenuhren ab. Die zeigen nämlich die wahre Sonnenzeit an. Räderuhren taugen also nicht, um mit dem Lauf der Sonne zu navigieren, es geht nur so, dass die von einer Räderuhr angezeigte Zeit als mittlere Zeit definiert und durch Addition der Zeitgleichung korrigiert wird.
Die Ordinate der Kurve im Bild 6 gibt mit den Winkeln eine Korrektur dafür an, wo die Sonne kulminiert, wenn die Uhrzeit in Greenwich 12:00 UT1 beträgt, am 11.2.2020 also auf Grt von etwa 360° – 3,5° = 356,5°. In Zeiten umgerechnet, also mit 4 multipliziert, sind das Korrekturzeiten, mit denen die mittlere Greenwicher Zeit GMT bzw. UT1 korrigiert werden muss, um die wahre Sonnenzeit zu erhalten, mit der dann auch navigiert werden kann. In einem Nautischen Jahrbuch oder Almanach wird mit dem Greenwichwinkel Grt bzw. GHA gearbeitet und in diesem ist die Zeitgleichung bereits berücksichtigt. Eine Korrektur der Chronometerzeit mit der Zeitgleichung war deshalb nur bei älteren Navigationsverfahren nötig, als es noch keine nautischen Jahrbücher gab.
4 Berechnungen
Praktische Astronavigation, Mathematik und Rechnen gehörten bisher immer zusammen. Durch Entwicklungen in der Computertechnik ist das allerdings immer weniger bis überhaupt nicht mehr erkennbar. Der Computer kann nämlich sämtliche Aufgaben mit Hilfe seiner Programme übernehmen, so dass am Ende nur noch die auf dem Sextanten abgelesenen Höhen eingegeben werden müssen. Die Ephemeriden werden ebenfalls gleich vom Programm berechnet oder aus einer Datenbank gezogen, ebenso wie die Sextantenbestückung. Ausgaben erfolgen grafisch auf einem Display mit einer Seekarte, in die man auch bequem hineinzoomen kann und darüber hinaus auch als Zahlenausgaben. Das entspricht der heutigen Arbeitsweise und das ist okay. Astronavigation soll Spass machen und keine Belastung sein.

Langweilig, sagt der Eine und purer Anachronismus. Wer wie die alten Seefahrer navigieren will, der soll auch genauso arbeiten und rechnen. Anstelle der Logarithmentafel wird die Benutzung des Taschenrechners gerade noch zugestanden.
Prima sagt der Andere, da kann ich endlich mit dem Sextanten navigieren, so wie das früher üblich war und endlich ohne Rechenstress. Diese romantische Navigationart gehört einfach zum Segeln dazu und ich kann sie jederzeit benutzen, ohne einen Astro-Lehrgang besuchen zu müssen. Außerdem kann ich mich dann problemlos auch ohne GPS auf dem Meer zurechtfinden falls doch mal was ausfällt.
Auch wenn der Computer, beispielsweise mit einer mobile App komplett alles übernimmt, kann es recht spannend sein, sich mit der Geschichte der Astronavigation, mit ihren Methoden und ebenso mit der dazugehörigen Mathematik auseinanderzusetzen.
Einen Hafen auf einer fernen Insel nur mit dem Sextanten und der Natur zu erreichen, kann auch für den verwöhnten GPS-Segler ein Erfolgserlebnis sein. Doch worauf gründen sich die Theorien der astronomischen Navigation?
Das mathematische Modell des Navigators ist das nautische Dreieck, das im Bild 8 dargestellt ist. Z kennzeichnet den Punkt, von dem aus wir die Sonne X am Vormittag in der östlichen Hemisphäre mit dem Sextanten beobachten. Das Dreieck besteht immer aus den drei Eckpunkten Standort, Bildpunkt und Pol (Nordpol oder Südpol). Natürlich gibt es auch andere Konstellationen, aber uns interessieren im Moment nur diese, mal mit der Sonne im Osten und dann im Westen. Im Bild ist alles Wichtige eingetragen. Horizont und Nullmeridian auf 0°. Unsere Standortbreite φ und die Deklination δ der Sonne bezeichnen die jeweiligen Entfernungen längs eines Meridians bis zum Horizont. Grt ist der Greenwicher Stundenwinkel und unter ![]() versteht man den Polwinkel, den Meridianunterschied zwischen Standortmeridian und Bildpunktmeridian. Wenn die Sonne im Westen beobachtet wird, ist die Polwinkel nach heutigem Verrständnis der Ortsstundenwinkel. Mit der Sonne im Osten erhält man den Ortsstundenwinkel als Ergänzung dieses Winkels zu 360° Weiter unten aber mehr dazu.
versteht man den Polwinkel, den Meridianunterschied zwischen Standortmeridian und Bildpunktmeridian. Wenn die Sonne im Westen beobachtet wird, ist die Polwinkel nach heutigem Verrständnis der Ortsstundenwinkel. Mit der Sonne im Osten erhält man den Ortsstundenwinkel als Ergänzung dieses Winkels zu 360° Weiter unten aber mehr dazu.
4.1 Mathematische Betrachtungen
In meinen Beiträgen zur astronomischen Navigation gibt es einige mathematische Abhandlungen. Viele schrecken gleich davor zurück. Mathematik und Formeln sind nicht jedermanns Sache.
Mathematik ist eigentlich nichts weiter als eine Kurzsprache, mit der viele Dinge in Natur und Technik exakter beschrieben werden können als mit vielen Worten. Das Auflösen und Umstellen von Gleichungen ist die Grammatik dieser Sprache. Bei genauem Hinsehen wird in allen Beiträgen eigentlich nur eine einzige Formel eingesetzt, und das ist der weiter unten beschriebene Kosinus Seitensatz, mit dem ein Dreieck auf einer Kugeloberfläche berechnet wird. Man muss sich also nur an diese ein Formel gewöhnen und an eine Umstellung davon und hat dann eigentlich keine Verständnisprobleme mehr. Gewöhnen muss man sich auch daran, dass alle Winkel und Distanzen mit Sinus oder Kosinus benannt werden. Das ist in der sphärischen Geometrie einfach so.
Rechnen ist dagegen eine ganz andere Disziplin, bei der man sich fürchterlich verheddern kann. So hört es sich einfach an, Winkel von Grad, Minuten und Sekunden in Dezimalgrade umzurechnen oder umgekehrt, aber ohne eine in Fleisch und Blut übergegangene Routine treten gerade dabei die meisten Probleme auf. Seekrankheit und Müdigkeit führen dann sogar zum Komplettausfall. Auf See soll und will heute niemand mehr rechnen.
4.2 Das Kugeldreieck
Unter Kugeldreiecken versteht man Dreiecke auf der Oberfläche einer Kugel. Die Erde ist eine Kugel und somit ist das nautische Dreieck im Bild 8 ein Kugeldreieck. Mit dieser geometrischen Figur wollen wir uns jetzt erstmal ganz allgemein auseinandersetzen und das ist tatsächlich einfacher als mancher denkt.
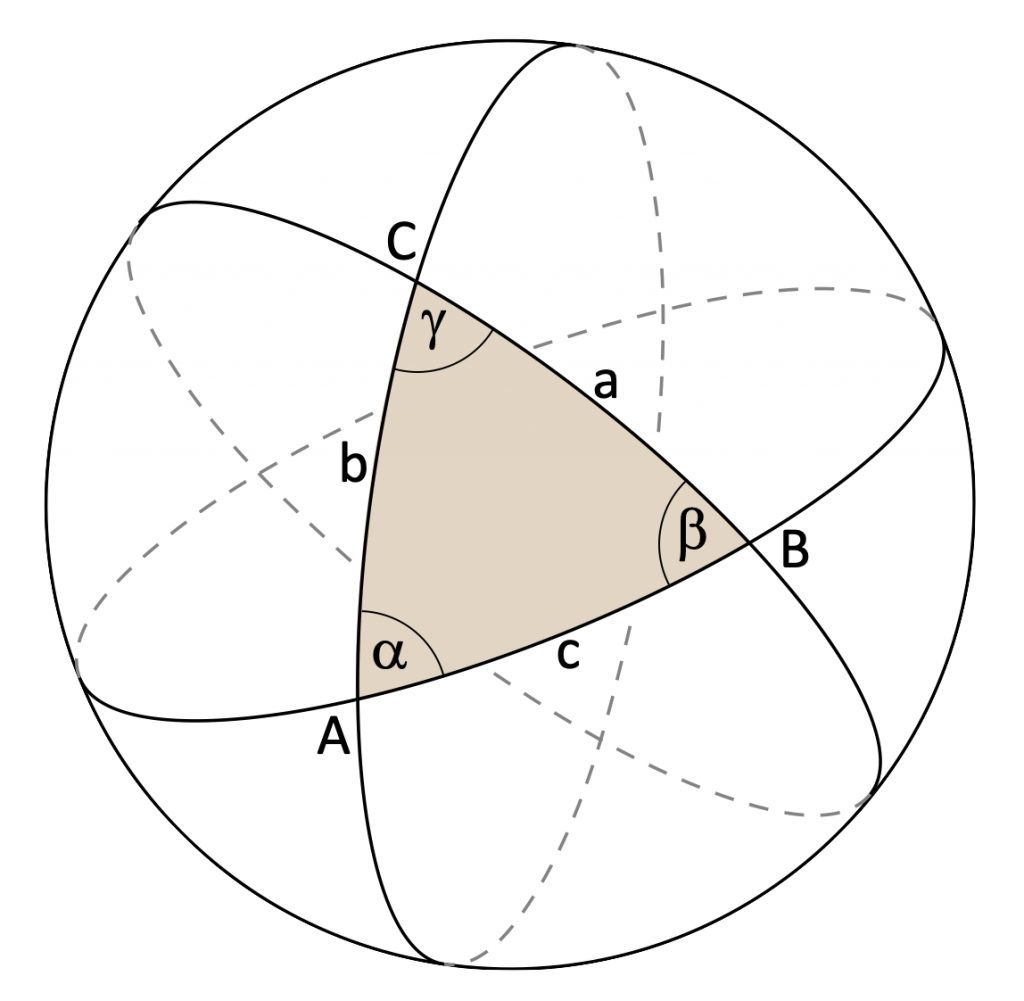
Wie bei einem Dreieck in der Ebene werden die drei Ecken mit den Großbuchstaben A, B und C bezeichnet. Die den Ecken gegenüberliegenden Seiten werden mit den entsprechenden Kleinbuchstaben a, b und c bezeichnet. Die Winkel tragen schließlich die Bezeichnungen α, β und ![]() . Das Dreieck besteht somit aus sechs Elementen, drei Winkeln und drei Seiten. Bild 9 zeigt dieses Dreieck auf einer Kugeloberfläche.
. Das Dreieck besteht somit aus sechs Elementen, drei Winkeln und drei Seiten. Bild 9 zeigt dieses Dreieck auf einer Kugeloberfläche.
Wie bei Dreiecken in der Ebene gilt auch bei einem Kugeldreieck, dass sich jedes fehlende Element berechnen lässt, sobald drei Elemente bekannt sind. Die Summe der Innenwinkel beträgt jedoch nicht 180 Grad, wie bei einem ebenen Dreieck, sie ist stets größer als 180 Grad.
Die Seiten von echten Kugeldreiecken sind Abschnitte auf Großkreisen. Im Gradnetz der Erde sind nur die Längenkreise und der Äquator Großkreise. Meridiane sind von Pol zu Pol laufende halbe Großkreise und ihre Länge beträgt 180°. Vom Äquator bis zum Pol sind es dann immer 90°. Auf einer Kugel ist die kürzeste Verbindung zwischen zwei Punkten immer eine Strecke, die einem Großkreis folgt. Wenn wir ein Gestirn beobachten, dann sehen wir es auf der kürzestmöglichen Verbindung. Der Blick durch das Fernrohr des Sextanten geht also immer in Richtung eines Großkreises.
Breitenkreise außer dem Äquator sind Kleinkreise weil ihr Umfang zu den Polen hin abnimmt. Abschnitte darauf können also keine Seiten unseres Kugeldreiecks sein. Wenn eine Peilung immer nur einen Großkreis entlang möglich ist, dann folgt daraus im Umkehrschluss, dass man in Richtung Osten oder Westen gar nicht wirklich peilen kann, es sei denn, man befindet sich auf dem Äquator.
Peilungen nach Ost oder West sind tatsächlich nur in einem begrenzten Sicht-Umkreis eines Beobachters möglich. Direkt am Nordpol sitzend hätte ein Breitenkreis nur wenige Meter Durchmesser und da wird es dann klar, dass eine Ost- oder Westpeilung einem Bogen folgen muss und somit unmöglich ist.
Bei Kugeldreiecken gibt es die Besonderheit, dass sowohl die Seiten als auch die Winkel in Grad gemessen werden. Auf der Erde werden schließlich alle Entfernungen in einem Gradnetz betrachtet, was alles ungemein vereinfacht. Umrechnungen sind nur immer dann nötig, wenn man ein Ergebnis unbedingt in Meilen haben will. Bezugsgröße auf der Erdkugel ist der Erdumfang mit 360°, was genau 21 500 nm sind. Dann sind 1° = 60 nm und 1′ = 1 nm oder Seemeile. Letztendlich dürfte es uns egal sein, wie Längern gemessen werden, in Kilometern Meilen oder Grad. Am Ende muss man sich entscheiden, ob umzurechnen ist.
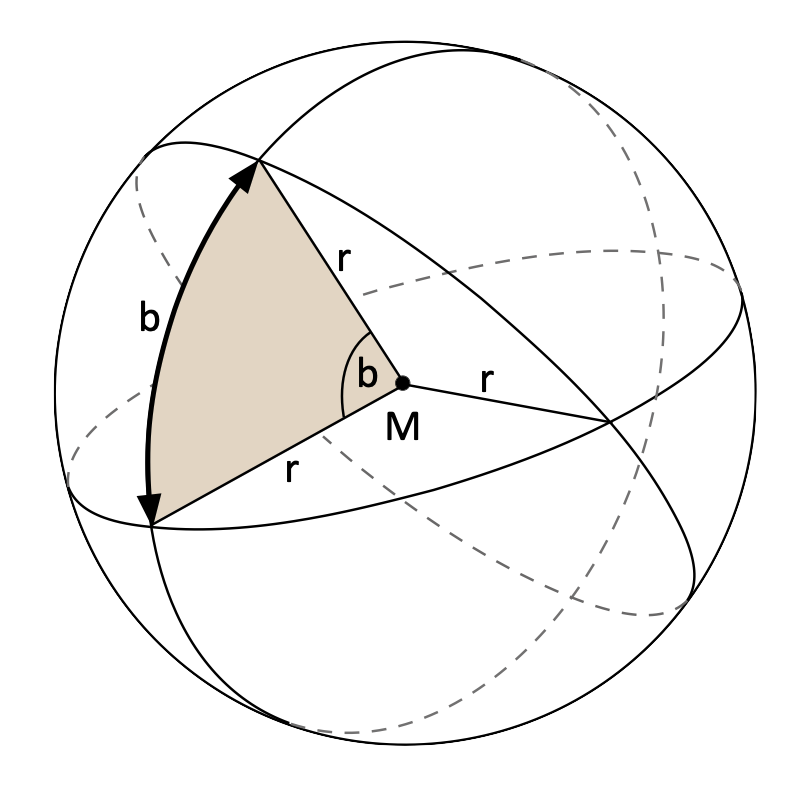
Ein Kugeldreieck bei dem Seiten und auch Winkel einheitlich in Grad gemessen werden, ist sogar noch einfacher zu berechnen als ein Dreieck in der Ebene wo die Winkel in Grad und die Seiten in Metern zu unterscheiden sind. Doch wie ist das zu erklären, dass auch die Seitenlängen in Grad gemessen werden? Bild 10 eröffnet einen Blick ins Innere der Erdkugel. Da ist der Erdradius mit r angegeben und der Winkel mit b. Dieser Winkel spannt auf der Erdoberfläche einen Bogen auf, der aufgrund dieser Verwandschaft ebenfalls die Länge b besitzt. Damit wird der Zusammenhang klar.
In den Formeln, die wir noch kennenlernen, kommen Seiten und Winkel nur als Sinus oder Kosinus vor. Das ist ungewohnt, aber wir sollten das erstmal einfach hinnehmen. Mit sin(z) und cos (????) kann man genauso umgehen, wie mit x und y. Wenn wir eine Seite oder einen Winkel ausrechnen wollen, dann bekommen wir deshalb auch immer nur den Sinus oder den Kosinus geliefert. Das macht aber gar nichts. Wir benutzen in diesem Fall einfach die Umkehrfunktion und schon haben wir die Seite oder den Winkel selbst. Wenn das Formelergebnis, beispielsweise die Länge einer gewünschten Seite q nur als cos q = 0,2618 erscheint, dann tippen wir auf unserem wissenschaftlichen Taschenrechnern auf die Taste mit der Bezeichnung cos-1 und schon erscheint als Ergebnis q = 15°. Auf der Erdoberfläche sind das q = 900 nautische Meilen.
Anstelle von cos-1 wird in Formeln meist die Funktion arccos benutzt, was genau dasselbe wie cos-1 ist. Analog dazu sind dann auch arcsin und sin-1 bzw. arctan und tan-1 dasselbe. Die Umkehrfunktionen liefern zu einem gegebenen Winkelfunktionswert den zugehörigen Winkel. In einem Kugeldreieck rechnet man also nicht die Länge einer Seite oder den Betrag eines Winkels aus, sondern den Kosinus einer Seite oder den Sinus eines Winkels oder umgekehrt. Das soll uns nicht stören. Wir benutzen anschließend einfach die Umkehrfunktion und erhalten dadurch den Betrag von Seite oder Winkel. Die Seitenlänge ist dann allerdings auch in Grad zu verstehen, aber das ist ja so üblich im Gradnetz der Erde wo ein Grad auf einem Großkreis 60 nm sind.
In allen Beiträgen zur Astronavigation, ob zur Bestimmung der Chronometerlänge, zur Standortbestimmung nach C. F. Gauß, zur Standortbestimmung nach T. H. Sumner und auch zur Standortbestimmung nach Saint Hilaire werden wir nur eine einzige Formel gebrauchen. Die gesamte Astronavigation, wie sie in mehr als zwei Jahrhunderten entwickelt wurde, beruht tatsächlich nur auf dem im Bild 8 gezeigten nautischen Dreieck. Um das zu berechnen braucht man eigentlich nur eine einzige Formel und das ist der Kosinus Seitensatz. Diese eine Formel könnte man sich, weil ein Dreieck drei Seiten und drei Winkel besitzt, in sechs Varianten vorstellen. Tatsächlich benutzt man aber nur zwei Varianten, für einen Winkel oder eine Seite und wechselt nur die Bezeichnungen, wenn der Winkel oder die Seite von einer anderen Ecke aus gesehen werden soll.
An einem Kugeldreieck wie im Bild 9 beschreibt dieser Formelsatz die Beziehung zwischen drei Seiten und einem Winkel. Das Verhältnis wird mit folgender mathematischer Gleichung beschrieben:
(1) ![]()
In Worten kann man das folgendermaßen ausdrücken:
Der Kosinus einer Seite ist gleich dem Produkt der Kosinusse der anderen beiden Seiten vermehrt um das mit dem Kosinus des Zwischenwinkels multiplizierte Produkt der Sinusse dieser beiden Seiten.
Übertragen auf die Seiten b und c muss dann geschrieben werden:
(2) ![]()
(3) ![]()
Das sind keine neuen Formeln. Es ist immer dieselbe Formel, nur von einer anderen Ecke des Dreiecks aus gesehen und deshalb mit den jeweils zuständigen Buchstaben geschrieben. Diese drei Formeln, stehen unter der Bezeichnung Kosinus Seitensatz in jedem besseren Formelbuch. Will man jetzt keine Seite, sondern einen Winkel ausrechnen, dann muss die Gleichung umgestellt werden. Das ist für Leute mit mathematischen Kenntnissen überhaupt kein Problem. Aufgrund der Bedeutung dieser Gleichung für sämtliche Navigationsmethoden soll das hier für Nicht-Mathematiker etwas ausführlicher geschehen.
Alle drei Seiten sollen bekannt sein und wir wollen den Winkel ![]() im Bild 8 ausrechnen. Wir wählen die Gl. 3, weil dort das
im Bild 8 ausrechnen. Wir wählen die Gl. 3, weil dort das ![]() schon geschrieben steht. Da es sich um Gleichungen handelt, muss auf beiden Seiten des Gleichheitszeichens immer das Gleiche gemacht werden. Zuerst subtrahieren wir auf beiden Seiten das Produkt
schon geschrieben steht. Da es sich um Gleichungen handelt, muss auf beiden Seiten des Gleichheitszeichens immer das Gleiche gemacht werden. Zuerst subtrahieren wir auf beiden Seiten das Produkt ![]() . Dadurch hebt es sich auf der rechten rechten Seite auf und bleibt auf der linken Seite als Subtrahend stehen:
. Dadurch hebt es sich auf der rechten rechten Seite auf und bleibt auf der linken Seite als Subtrahend stehen:
![]()
jetzt müssen wir ![]() freistellen. Dazu dividieren wir beide Seiten der Gleichung durch
freistellen. Dazu dividieren wir beide Seiten der Gleichung durch ![]() . Die Folge ist, dass sich dieser Term auf der rechten Seite rauskürzt und links als Nenner bleibt:
. Die Folge ist, dass sich dieser Term auf der rechten Seite rauskürzt und links als Nenner bleibt:
![]()
Schließlich wenden wir gleich noch die Umkehrfunktion an und machen aus dem Kosinus des Winkels ![]() gleich den Winkel
gleich den Winkel ![]() :
:
(4) ![]()
Auch in dieser Form wird uns der Kosinus Seitensatz begegnen und zwar immer dann, wenn ein Winkel ausgerechnet werden muss, wie z. B. das Azimut, die Peilung auf den Bildpunkt eines Gestirns.
4.2.1 Komplementwinkel
Wenn wir jetzt den Winkel ![]() im Bild 8 berechnen wollten, dann müssten für die Dreieckseiten die Ausdrücke 90° – φ, 90° – δ und 90° – h eingesetzt werden, wodurch die Formel recht lang wird. Zur Erinnerung, δ ist die Deklination der Sonne zum Beobachtungszeitpunkt und h die beobachtete Höhe. Die eigene Standortbreite φ kennen wir nur ungefähr, z. B. aus der letzten Mittagsbreite oder der letzten Nordsternbreite nach einer durchgeführten Koppelnavigation. Hier werden jetzt die Komplementwinkel oder einfach Komplemente verwendet. Ein Komplementwinkel ist seine Differenz zu 90°. Das hatten wir schon im Bild 2 kennengelernt. Dort gibt es die gemessene Höhe h = 90° – s und den Zenitabstand s = 90° – h. Die Höhe h ist also das Komplement zum Zenitabstand s und umgekehrt. Analog trifft das dann für alle anderen Seiten ebenfalls zu. Das Komplement von 90° – φ ist φ und das Komplement von 90° – δ ist δ. In der nachfolgenden Tabelle sind die Seitenlängen der Dreiecke zusammengefasst:
im Bild 8 berechnen wollten, dann müssten für die Dreieckseiten die Ausdrücke 90° – φ, 90° – δ und 90° – h eingesetzt werden, wodurch die Formel recht lang wird. Zur Erinnerung, δ ist die Deklination der Sonne zum Beobachtungszeitpunkt und h die beobachtete Höhe. Die eigene Standortbreite φ kennen wir nur ungefähr, z. B. aus der letzten Mittagsbreite oder der letzten Nordsternbreite nach einer durchgeführten Koppelnavigation. Hier werden jetzt die Komplementwinkel oder einfach Komplemente verwendet. Ein Komplementwinkel ist seine Differenz zu 90°. Das hatten wir schon im Bild 2 kennengelernt. Dort gibt es die gemessene Höhe h = 90° – s und den Zenitabstand s = 90° – h. Die Höhe h ist also das Komplement zum Zenitabstand s und umgekehrt. Analog trifft das dann für alle anderen Seiten ebenfalls zu. Das Komplement von 90° – φ ist φ und das Komplement von 90° – δ ist δ. In der nachfolgenden Tabelle sind die Seitenlängen der Dreiecke zusammengefasst:
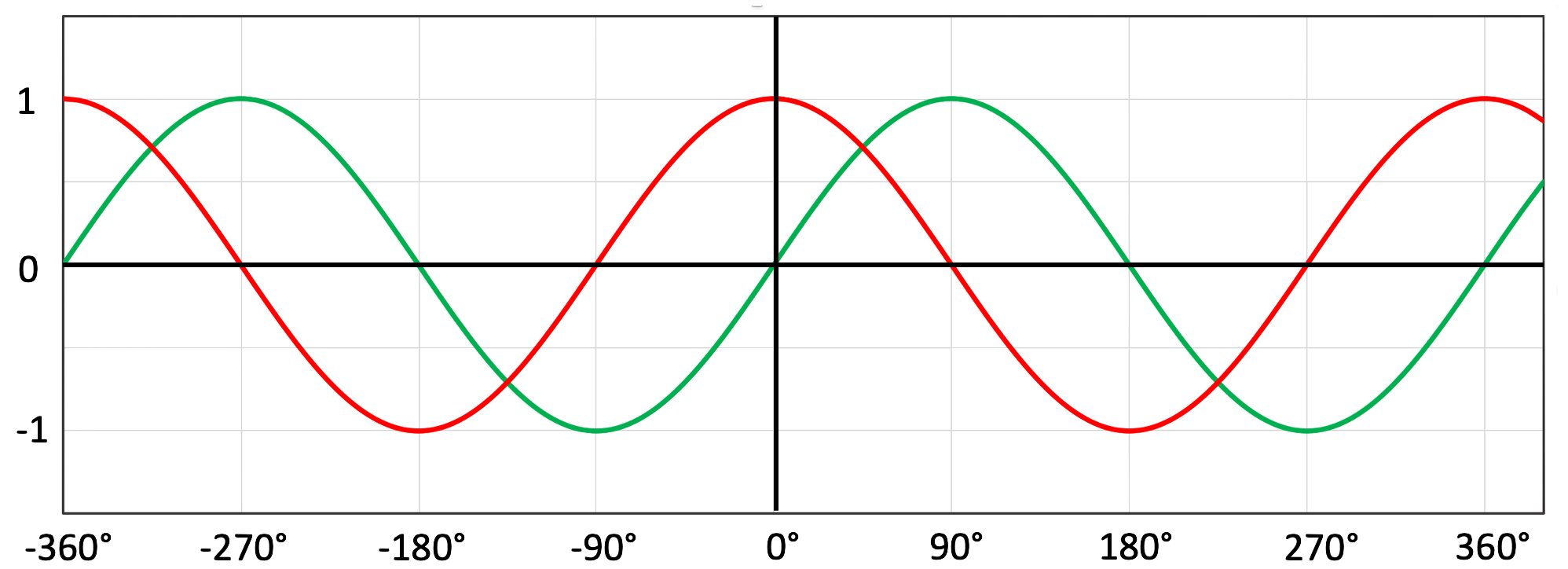
Das kommt daher, weil die Sinusfunktion und die Kosinusfunktion um 90° in der Phase verschoben sind, wie im Bil 11 zu sehen ist und daher gilt:
Unter Anwendung der Komplementwinkel kehrt sich also die Sinusfunktion eines Winkels in die Kosinusfunktion des Komplementwinkels und umgekehrt. Das werden wir bei allen Methoden der Standortberechnung wiederfinden und ist deshalb an dieser Stelle besonders erwähnt. Wenn wir jetzt also die Gleichung 4 nehmen, mit der wir gerade den Winkel ![]() berechnet haben, um damit jetzt den Winkel
berechnet haben, um damit jetzt den Winkel ![]() im Bild 8 zu berechnen, dann lautet diese Gleichung ohne Benutzung der Komplemente:
im Bild 8 zu berechnen, dann lautet diese Gleichung ohne Benutzung der Komplemente:
![]()
Nutzen wir jetzt die Komplementwinkel, dann drehen sich sin in cos und (90° – a) in a und alles sieht einfacher aus:
(5) ![]()
Die Summe aus diesem Winkel ![]() und dem Stundenwinkel Grt ist direkt die Standortlänge
und dem Stundenwinkel Grt ist direkt die Standortlänge ![]() .
.
Hier ist jedoch noch einiges zu beachten, weil Grt von 0 bis 360° in Westrichtung um die ganze Erde zählt, das Gradnetz der Erde aber schon vor mehr als 2000 Jahren in 180 Westgrade und 180 Ostgrade aufgeteilt worden ist, was in einigen Fällen noch einer kleinen Korrektur bedarf.
4.2.2 Das Azimut
Das Azimut ist die rechtweisende Peilung auf den Bildpunkt der Sonne und ist im Bild 8 als Az eingezeichnet. So wie vorstehend der Winkel ![]() berechnet wurde kann jetzt auch das Azimut Az berechnet werden, also mit genau dem gleichen Formelaufbau, der sich jetzt nur entgegen der Uhrzeigerrichtung um einen Winkel bzw. eine Seite weiterdreht. Wir erhalten für diesem Fall:
berechnet wurde kann jetzt auch das Azimut Az berechnet werden, also mit genau dem gleichen Formelaufbau, der sich jetzt nur entgegen der Uhrzeigerrichtung um einen Winkel bzw. eine Seite weiterdreht. Wir erhalten für diesem Fall:
(6) ![]()
Die Kennzeichnung des Azimuts in dieser Gleichung mit einem Stern hat folgenden Hintergrund. Das Azimut wird hier als rechtweisend Nord angegeben (ganz selten findet man auch eine Angabe als rechtweisend Süd). Das bedeutet, dass es der Winkel zwischen dem Nordmeridian b und der Peilung s in Richtung Sonne sein muss und zwar als rechtsdrehender Winkel. Genauso wie Kursangaben.
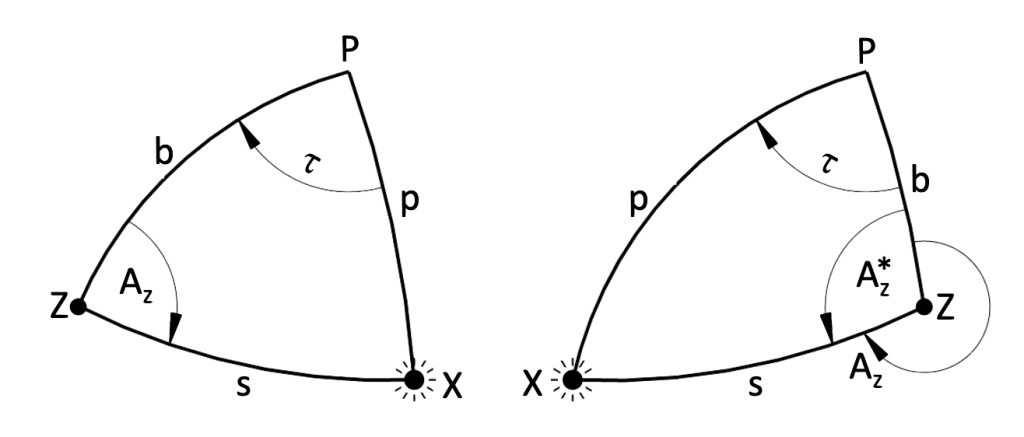
Das bedeutet dass nach dem Schiffsmittag, wenn die Sonne den Standortmeridian überholt hat, die Seite s von Ost nach West umschlägt, wie das im Bild 12 rechts zu sehen ist. Der Kosinus Seitensatz berechnet jedoch nur immer die Innenwinkel in dem Dreieck. Nach dem Schiffsmittag ist das Azimut entsprechend seiner Definition jedoch der Außenwinkel. Das ist kein Problem. Wir müssen in dem Fall, wenn der Schiffsmittag vorbei ist, den berechneten Winkel von 360° subtrahieren, um das Azimut zu erhalten. Das Azimut wird u. A. gebraucht, um Versegelungen zu berücksichtigen, wenn also zwischen den Höhenmessungen zur Standortbestimmung Ortsveränderungen auftreten.
In der Methode nach Saint Hilaire spielen das Azimut und die rechnerische Höhe für einen geschätzten Standort die zentrale Rolle. Das mit der Gl. 6 gezeigte Azimut ist das sogenannte Höhenazimut. Es wird berechnet, indem die Höhe h gemäß der nachfolgenden Gl. 7 eingesetzt wird. Im Höhenverfahren nach Hilaire wird jedoch gern das sogenannte Zeitazimut eingesetzt. Diese Formel ist etwas komplizierter und das Ergebnis muss dann nicht nur hinsichtlich Ost oder West sondern hinsichtlich aller Quadranten eingeordnet werden. Dieses Vorgehen ist nicht ganz verständlich, weil bei der Berechnung des Höhenazimuts für einen bekannten Standort keine Messwerte eingesetzt werden.
4.2.3 Die Höhenformel
Unsere nächste Aufgabe besteht darin, für einen bekannten Ort, dessen Länge und Breite vorliegen, auszurechnen, wie hoch die Sonne zu einem bestimmten Zeitpunkt dort über dem Horizont steht. Die Höhe h ist das Komplement der Seite s. Um die auszurechnen, braucht man also drei bekannte Elemente des PZX-Dreiecks. Bekannt sind schon mal die Seiten p und b. Man bräuchte jetzt am besten den davon eingeschlossenen Winkel ![]() . Doch der ist nicht direkt zu haben. Die Lösung dafür ist im Bild 13 zu erkennen. Dort haben wir einen Winkel t eingeführt.
. Doch der ist nicht direkt zu haben. Die Lösung dafür ist im Bild 13 zu erkennen. Dort haben wir einen Winkel t eingeführt.
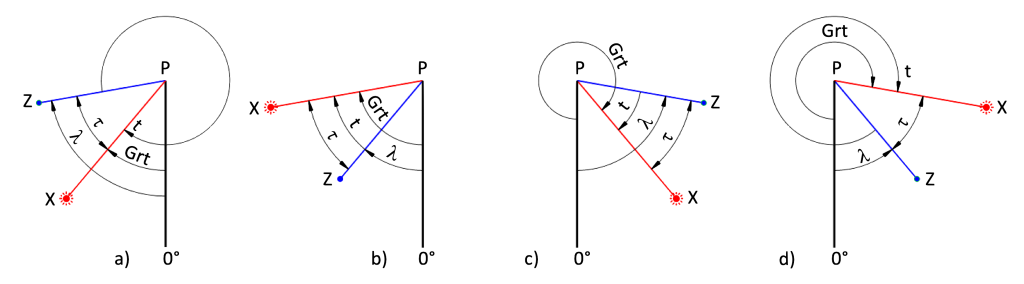
Dieser Winkel t ist der Ortsstundenwinkel (engl. LHA = Local Hour Angle). Es ist der Stundenwinkel eines beliebigen Ortes und zählt in westliche Richtung gehend vom Meridian des benannten Ortes bis zum Meridian des Bildpunktes der Sonne. Der Greenwicher Stundenwinkel Grt ist somit der Ortsstundenwinkel des Ortes Greenwich. Im Bild 13 in b) und c) ist dieser Winkel identisch mit ![]() . In a) und d) ist er die Ergänzung zu 360°.
. In a) und d) ist er die Ergänzung zu 360°.
Um die Seite s im Bild 12 ausrechnen zu können, würden wir die Gl. 3 wählen. Dort wird der Kosinus des Polwinkels benutzt. Die Kosinusfunktion ist, wie Bild 11 zeigt, symmetrisch zur Ordinate, also zu 0° und liefert deshalb alle 360° vor oder zurück immer wieder denselben Wert. So ist es nicht nötig, den Winkel t bzw. LHA explizit ausrechnen zu müssen. Wir können bereits die Summe von Grt und λ verwenden. Grt + λ ist nicht gleich t, aber cos(Grt + λ) ist gleich cos (t). Wenn die entsprechenden Werte in die Gl. 3 eingesetzt werden, erhält man:
![]()
Nach Ersetzen der Seiten durch die Komplementwinkel und ![]() mit Grt +
mit Grt + ![]() folgt weiter:
folgt weiter:
![]()
Schließlich erhalten wir die bekannte Höhenformel:
(7) ![]()
In der Literatur steht anstelle cos (Grt + λ) meist ![]() .
.
Eigentlich ist das, was hier im Abschnitt 4 an Mathematik gezeigt wurde, alles was man braucht, um sämtliche bekannten Navigationsmethoden verstehen zu können. Ob das die Lösung der Zweihöhenmethode nach Gauß oder die Hilaire Methode ist, mehr als die hier gezeigten Gleichungen werden darin nicht benutzt. Die dahinter stehende Mathematik ist also sehr übersichtlich. In der Praxis treten Schwierigkeiten meist immer dann auf, wenn Zahlen in die Formeln eingesetzt werden müssen. Die Umrechnung von Grad und Minuten in Dezimalgrade oder ins Bogenmass und zurück birgt doch erhebliches Verwirrungspotential. Wer darin keine Routine hat, der kann schon leicht verzweifeln, weil es einfach nicht gelingt, zu einem vernünftigen Ergebnis zu kommen.
Links:
nach oben ♦ Mittagsbreite und Chronometerlänge ♦ Gauß und das Zweihöhenporoblem ♦ Thomas H. Sumner, Begründer der Standliniennavigation ♦ Die Methode des Marcq Saint Hilaire ♦ Navigieren mit Excel ♦ Ein wenig Sextantenkunde ♦ Sextantentest Mark 25 ♦ Downloads ♦ Home