John Harrisons H1 aus dem Jahre 1759. Die Entwicklung der Schiffschronometer war Voraussetzung für das Entstehen der modernen Astronavigation
Thomas Hubbard Sumner wurde 1807 als Sohn eines Architekten in Boston, Massachusetts geboren. Im Alter von 15 Jahren begann er ein Studium an der Havard Universität, das er vier Jahre später abschloss. Im Jahr 1829 heuerte er als Seemann auf einem Handelsschiff auf der China Route an. Acht Jahre später war er Kapitän mit einem eigenen Schiff. Sumner hatte eine sehr gute Ausbildung und verfügte über weitreichende Kenntnisse in Mathematik und Astronomie. Er ist der Begründer der Standliniennavigation und seine Arbeit gilt als der Beginn der sogenannten „moderne Astronavigation“. Zwei amerikanische Forschungsschiffe, ein Mondkrater und ein Gletscher in der Antarktis wurden nach ihm benannt. Die Navigation mit linearen Standlinien (Line of Position Navigation) wurde 30 Jahre später von dem französischen Seeoffizier Saint Hilaire perfektioniert, was zu einer erheblichen Verbesserung in der Genauigkeit führte. Die Hilaire Methode entwickelte sich zum Standard in der astronomischen Navigation und wurde erst von der Satellitennavigation abgelöst. Bis heute gilt sie als offizielle Backup Methode. Sumners persönliches Schicksal endete tragisch. Im Jahr 1850 kam er in ein Krankenhaus für Psychiatrie und 5 Jahre später in ein Irrenhaus, wo er im Alter von 69 Jahren verstarb.
1 Ein Zufall kommt zu Hilfe
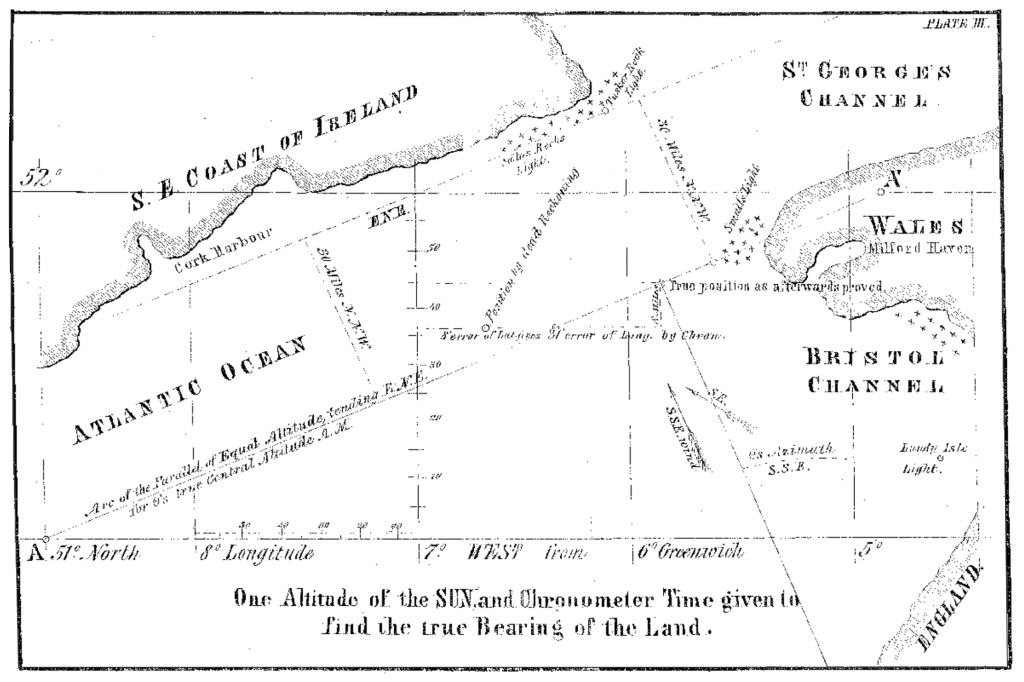
Am Morgen des 17. Dezember 1837 näherte sich Kapitän Sumner, er war schon 22 Tage von South Carolina kommend auf See, dem St. George Kanal zwischen Irland und Wales. Seine Reise ging nach Greenock in Schottland. Es stürmte und es war bedeckt. Er brauchte jetzt dringend Sicherheit darüber, dass ihn der Wind aus SSE nicht zu weit an die gefährlich flache und steinige Südostküste von Irland versetzt hat. Etwa um 10:15 riss die Wolkendecke plötzlich auf und die Sonne wurde sichtbar. Es reichte gerade für eine Messung des Kimmabstandes der Sonne.
Die Methoden zur Bestimmung der Mittagsbreite und der Chronometerlänge waren zu Beginn des 19. Jahrhunderts auf allen Seeschiffen gut etabliert. Eine Längenbestimmung zur Mittagszeit ist jedoch nicht möglich. Auf ihrer Kulminationshöhe beschreibt die Sonne einen sehr flachen Bogen. Sie legt dabei mehr als 100 Meilen in Ost-West Richtung zurück, ohne dass eine Höhenänderung festgestellt werden kann. Die Breite hingegen ändert sich in dieser Zeit kaum, so dass Fehler in der Breite nur sehr gering sind. Wenn die Höhe der Sonne zwei Stunden vor oder nach dem Schiffsmittag gemessen wird, dann würde eine Längenberechnung auf Grundlage einer vorliegenden Breite nur einen kleinen Fehler verursachen.

Kapitän Sumner war sich dessen bewusst. Deshalb war es ein großes Glück, dass er die Höhe der Sonne noch zwei Stunden vor dem Schiffsmittag messen konnte. Er machte sich Sorgen um seine Position, weil ihn die starken Winde in Richtung der irischen Lee-Küste getrieben haben konnten. Sein Kurs war zu diesem Zeitpunkt ENE und er hatte nur eine ältere DR Position (Koppelposition).
Aus der gemessenen Höhe und der DR Latitude konnte er jetzt eine Chronometerlänge und damit seine Position errechnen. Die lag dann sogar östlich von seiner DR Position und somit weiter und sicherer von der irischen Küste entfernt als seine DR Position. Als vorsichtiger Seefahrer wusste er aber auch, dass die so ermittelte Position einen erheblichen Fehler aufweisen konnte, denn die Breite, die seiner Berechnung zugrunde lag war nur gekoppelt und somit geschätzt und konnte falsch sein. Also versuchte er herauszufinden, was die Konsequenzen dieses Fehlers wären.
Unter Verwendung derselben gemessenen Höhe und einer Breite, die diesmal 10 Meilen weiter nördlich und damit noch näher an der gefährlichen Lee-Küste Irlands lag, berechnete er eine zweite Position. Dabei fand er jedoch eine Position, die unerwartet noch weiter östlich lag als die vorherige. Eine dritte Berechnung mit einer angenommenen Breite, die um weitere 10 Meilen nördlicher lag, ergab dann eine dritte Länge die ebenfalls noch weiter östlich als die beiden vorherigen lag. Mit diesen Ergebnissen ging Kapitän Sumner in seine Karte und sah, dass sich alle drei errechneten Positionen auf einer geraden Linie befanden. Da wurde ihm klar, dass diese Linie ein kleines Stück der Kreislinie einer Höhengleiche ist. Höhengleichen waren ihm bekannt. Man fand sie sogar schon auf uralten Astrolabien. Eine Senkrechte auf dieser Linie musste das Azimut zur Sonne sein. Jeder Beobachter auf dieser Linie hätte die Sonne zur selben Zeit in derselben Höhe beobachten können und sein Schiff befand sich irgendwo auf dieser Linie.
Es war einer dieser ungewöhnlichen Zufälle in der Geschichte. Die erhaltene Linie war nicht nur fast mit seiner Kurslinie identisch, sondern lief auch direkt auf den Leuchtturm “Small’s Rocks” zu. Das ist ein wichtiges Seezeichen vor der Westküste von Wales. Kapitän Sumner entschloss sich, den Kurs entlang der entdeckten Linie beizubehalten, auf der früher oder später der Leuchtturm “Small’s Rocks” gesichtet werden würde. Einige Zeit später wurde der Leuchtturm trotz des dichten Wetters tatsächlich entdeckt und die Reise konnte dann sicher entlang der Westküste Englands fortgesetzt werden.
Das war neu. Nach nur einer einzigen Beobachtung eines Gestirns konnten zwei Breiten gewählt und es konnte berechnet werden, welche Längen diese Breiten bei derselben Gestirnshöhe kreuzen. Das lieferte zwei Punkte auf einer Karte und wenn man diese miteinander verband, so hatte man eine Linie, auf der sich das Schiff befinden musste, eine Standlinie. Sumner hat erkannt, dass seine Standlinie ein kurzer Abschnitt vom Kreis der Höhengleiche ist und dass er mit seinen Berechnungen eine dicht an der Peripherie liegende Sekante an die Höhengleiche konstruiert hatte.
Diese konnte man auch verlängern und sah dann auf der Karte, wo sie hinführte. So konnten von einer Standlinie Kurse abgeleitet werden, die sicher parallel an einer unsichtbaren Küste entlang führten, oder sogar direkt auf Land zusteuerten. Außerdem konnten an einem Tag zwei Standlinien bestimmt werden, wenn man die Höhe der Sonne einmal vormittags und dann nachmittags bestimmte. Der eigene Standort muss dann im Sinne einer Kreuzpeilung dort sein, wo sich die Standlinien kreuzten. All das veranlasste Sumner, ein Buch zu schreiben, das 1843 unter dem Titel “A NEW METHOD OF FINDING A SHIP’S POSITION AT SEA“ erschien.
Die Methode war überaus einleuchtend und wurde von den Seeleuten sofort angenommen. Die auszuführenden Berechnungen waren zudem identisch mit denen, die längst schon zur Bestimmung der Chronometerlänge angewendet wurden und damit waren die Navigatoren gut vertraut. Die Chronometerlänge selbst ergab mit der geschätzen Breite nur einen Punkt. Man musste nochmal mit einer anderen Breite rechnen und hatte dann einen zweiten Punkt. Eine Linie durch beide Punkte war die Standlinie. Somit war erstmalig eine Möglichkeit gefunden, unabhängig vom Schiffsmittag, zu beliebigen Zeiten ohne Landsicht auf See mit einfachen Mitteln einen Standort zu finden.
In den USA widmete man der Sumner’schen Methode eine geradezu offizielle Aufmerksamkeit. Das nautische Institut zu Boston ernannte ein Comité zur Prüfung der Methode, welche zu dem Ergebnis kam, dass die Methode auf vollkommen richtigen Grundsätzen basiert. Man sah in dieser Methode den Beginn einer neuen Ära in der praktischen Navigation. Das hatte auch nochmal eine Verbesserung der Chronometerproduktion zur Folge. In der US-Marine wurde der Befehl erteilt, jedes Schiff so auszustatten, dass mit der Sumner’schen Methode navigiert werden konnte. Im Jahre 1844 gelangte die Methode nach England und von dort in die englischen Kolonien im Pazifik und im Orient. Nur in Frankreich wurde die Methode erst einige Jahre später benutzt.
2 Navigieren mit Sumnerlinien
Kapitän Sumner war ein bescheidener und praktisch denkender Seemann. So legte er zunächst weniger Gewicht auf die Tatsache, dass er mit seiner Methode eine Lösung des Zweihöhenproblems gefunden hatte. Er war vielmehr froh, ein Mittel geliefert zu haben, mit dem in kritischen Fällen Genaueres über den Ort des Schiffes ermittelt werden konnte. Genau darin sah er den Kern seiner Methode. So schrieb er in der Einleitung zu seinem Buch:
„Der Zweck dieses Werkes ist weniger, dem Seefahrer eine neue Methode von „doppelten Höhen“ vorzulegen, als ihm eine genaue Methode zu verschaffen, durch eine Höhe der Sonne, zu irgend einer Stunde des Tages genommen, mit der Chronometerzeit die wahre Richtung eines Landes zu finden … „
Er sah das Wesen der „neueren Astronomie“, wie die Franzosen den Beginn dieser aufkommenden Ära formulierten, in der Ausnützung einer einzigen Höhe für die Bestimmung der wahrscheinlichsten Schiffsposition. Der Begriff „Schiffsposition“ wurde nicht mehr als Punkt verstanden, sondern irgendwo auf einer bekannten Linie gesehen, die eine bekannte Kursrichtung aufwies. Die Lösung des Zweihöhenproblem wurde damit auf andere Bahnen gelenkt, die mehr und mehr praktischen Gesichtspunkten folgten. Grafische Lösungsverfahren waren jetzt auch in der Hochseenavigation möglich geworden. Diese Entwicklung hatte die Eigenschaft, alles Alte und somit die bisherigen mathematisch analytischen Ansätze und Lösungen zu verdrängen.
Obwohl Sumner den Nutzen seiner Methode vor allem in der einen Standlinie sah, die einen wahren Kurs vorgab, von dem der eigene Kurs dann sicher abzuleiten war, beschrieb er auch das Finden eines Standortes durch Kreuzung zweier Standlinien, was wir uns nun etwas genauer anschauen wollen. Dazu dient der Text aus seinem Buch in deutscher Übersetzung. Dort steht unter Rule 1:
- Wähle zwei ganzzahlige Breiten, wobei eine davon die nächst kleinere und die andere die nächstgrößere ist als die gekoppelte Breite.
- Finde in der üblichen Weise die Schiffslänge nach Chronometer unter der Annahme, das Schiff befände sich auf der kleineren Breite und markiere die gefundene Position als Punkt A auf der Karte.
- Finde in derselben Weise die Schiffsposition unter der Annahme, es befindet sich auf der größeren Breite und markiere die gefundene Position als Punkt A‘ auf der Karte.
- Verbinde diese zwei Punkte mit einer geraden Linie, die so lang wie nötig ist. Diese Linie ist der Bogen einer Höhengleiche und durchquert die wahre Position des Schiffes und …
Sumner drückt damit aus, dass die gefundene Linie ein Stück des Kreisbogens einer Höhengleiche ist. Die Ersetzung des Kreisbogens mit einer geraden Linie war für ihn gerechtfertigt unter der Voraussetzung, dass der Bildpunkt des beobachteten Gestirns weit genug weg ist. Die Originalkarte im Bild 2.1 zeigt die von ihm gezeichnete Linie und die mit A bzw. A‘ bezeichneten Schnittpunkte auf den Breitengraden 51° und 52°. Sumner betont weiter, dass eine Senkrechte von der Linie AA‘ ausgehend auf der Seite der Sonne, das Azimut auf den Bildpunkt der Sonne ist. Unter Rule. beschreibt Sumner dann die Fortsetzung für den Fall, dass eine Positionsbestimmung ohne Landsicht vorgenommen wird, wobei er voraussetzt, dass die erste Höhenmessung am Vormittag und die zweite am Schiffsnachmittag erfolgen und die gleichen wie unter Rule I. gewählten Breiten zugrunde liegen. Nachfolgend wieder der Text in der Übersetzung:
- Vorzugehen ist wie in Rule I, wo entsprechend der ersten Beobachtung die Linie AA‘ projiziert wurde.
- Gehe in exakt derselben Weise vor, um die zweite gerade Linie zu projizieren (benutze dieselben angenommenen Breiten wie zuvor) und die zweite Linie wird der zweiten Beobachtung entsprechen. Bezeichne die zwei auf den angenommenen Breiten gefundenen Positionen als B und B‘.
- Die zwei geraden Linien werden sich einander schneiden, meistens zwischen den angenommenen Breiten. Sollten sie das nicht tun, dann bringe sie zum Schneiden (Anm. verlängern) und der Schnittpunkt ist der Längengrad und der Breitengrad der Schiffsposition sofern der Schiffsort zwischen den Beobachtungen nicht verändert wurde.
- Wenn das Schiff seine Position geändert hat dann setze die zwischen den Beobachtungen gesegelte Entfernung in Kursrichtung von einem beliebigen Punkt der Linie AA‘ ab. Zeichne durch diesen Zielpunkt eine gerade Linie parallel zur Linie AA‘ bis diese sich mit der Linie BB‘ schneidet. Dieser neue Schnittpunkt mit BB‘ ist die Schiffsposition zum Zeitpunkt der zweiten Beobachtung.
Sumner hatte also auch schon die Lösung für eine Versegelung eines Standortes und die klingt logisch. Wenn der Schiffsort irgend ein Punkt auf einer Standlinie ist, dann müssten alle Punkte gleichermaßen versegelt worden sein, was durch Parallelverschiebung der gesamten Linie gemacht wird. Mit dieser Methode war es nun einfach geworden, den Standort sogar mehrfach am Tage bestimmen zu können. Man war nicht mehr nur auf die Mittagszeit angewiesen. Das wurde auch immer wichtiger, denn die Schiffe wurden immer schneller, es gab Dampfschiffe, die mit mehr als 20 Knoten liefen und es musste sichergestellt werden, dass diese immer dem wirtschaftlichsten Kurs folgten. Nur um die Mittagszeit selbst herum konnte ein Standort kaum bestimmt werden. Das betrifft übrigens alle Methoden. Am Schiffsmittag hat die Höhengleiche ihren kleinsten Durchmesser und der Standort ist der nördlichste (oder südlichste) Punkt darauf. Noch nördlicher (oder südlicher) wird keine Breite mehr von der Höhengleiche berührt. Die Extrempunkte einer Höhengleiche lassen sich einfach berechnen (h = beobachtete Höhe). Beim Erreichen dieser Höhe ist Schiffsmittag.
- nördlichster Punkt:
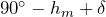
- südlichster Punkt:
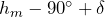
Mit seiner Methode begründete Thomas Sumner die Standliniennavigation. Seine Standlinien wurden damals auch als Sumnerlinien bezeichnet. Saint Hilaire benutzte 40 Jahre später ebenfalls gerade Standlinien. Er schaffte es jedoch, diese als Tangente an den Kreis der Höhengleiche zu bringen. Die Möglichkeit den Schnittpunkt zweier sich überlappender Kreise oder die Schnittpunkte zweier Kreisbögen zu berechnen schien damals als zu aufwändig, jedenfalls an Bord. Man war übereingekommen, dass die Krümmung einer Höhengleiche, im näheren Standortbereich so gering ist, dass die Annahme von Geraden gerechtfertigt ist. Dadurch entstehen Standortfehler, die nur im Extremfall einige Meilen betragen können. Die Praktiker und Seefahrer hatten damit die Lösung des Zweihöhenproblem für sich entschieden.
3 Berechnungen
Die Formeln zur Berechnung einer Sumnerlinie waren identisch mit denen zur Berechnung einer Chronometerlänge. Dieselbe Formel muss nur zweimal benutzt werden, um eine Standlinie zu berechnen und viermal, um einen Standort aus zwei sich kreuzenden Standlinien zu erhalten. Die Formel war den Seeleuten damals gut bekannt und geläufig. Und auch der gesamte Zusammenhang war ihnen logisch und problemlos überschaubar. Zunächst musste ein Polwinkel bzw. Stundenwinkel berechnet werden. Das ist bekanntlich die Differenz zwischen dem Standortmeridian und dem Meridian des betrachteten Gestirns. Dazu brauchte man die Deklination, beispielsweise der Sonne, die man aus einem Almanac entnahm und deren Höhe, die mit einen Sextanten oder Oktanten gemessen werden konnte. Weiterhin brauchte man die Breite, auf der das Schiff stand. Diese ließ sich als Mittagsbreite oder Nordsternbreite leicht bestimmen und stand in der Folgezeit als Koppelbreite zur Verfügung.
Sumner hatte für die Durchführung seiner Berechnungen nur Logarithmentafeln zur Verfügung. Die grundsätzliche Art der Berechnung der Längen auf dieser Grundlage wurde im Beitrag Mittgsbreite und Chronometerlänge beschrieben. Sumner benutzte jedoch eine etwas verkürzte Form für die Berechnung der Stundenwinkel, die nachfolgend vorgestellt wird.
3.1 Logarithmisch mit abgeleiteter Gleichung
Für die logarithmische Berechnung des Stundenwinkels nach West oder nach Ost bzw. der Zeit, die der Bildpunkt benötigt, einen dieser Stundenwinkel zu durchstreichen, kann von der Gl. 3 in Mittagsbreite und Chronometerlänge ausgegangen werden. Sie lautet leicht umgestellt:
(1) ![]()
Nach Multiplikation beider Seiten der Gleichung mit -1 und Anwenden der Sekantenfunktion sec x = 1/cos x auf cos ???? und cos ???? erhält man daraus
(2) ![]()
Mit dieser abgeleiteten Gleichung ist das im Bild 3 gezeigte Schema aus dem Buch von Sumner nachvollziehbar. Er beschreibt darin die Situation an jenem denkwürdigen Tag, dem 17. Dez. 1837, zwischen Irland und England, rechnet aber mit anderen Breiten. In der oberen Hälfte wird die Standortlänge berechnet, wenn die geschätzte Breite 51° N betragen würde und in der unteren Hälfte die Standortlänge, wenn die Breite 52° N wäre. Zum Verständnis reicht eine Betrachtung der oberen Hälfte. Lat. und Dec. sind Breite und Deklination und Sum. die daraus berechnete Meridiandistanz (![]() –
– ![]() ). Das ist der Abstand zwischen Standortbreite und Deklination längs eines Meridians. Haben beide das gleiche Vorzeichen, dann wird der Betrag des kleineren Wertes vom Betrag des größeren subtrahiert. Bei ungleichen Vorzeichen werden die Beträge beider Werte addiert. Es fällt auf, dass in der Rechnungsaufstellung von Sumner der mit der eckigen Klammer eingeschlossene Faktor in Gl. 2 mit 105 multipliziert ist, indem die Elemente nat. cos. und nat. sin. mit dem Faktor 105 multipliziert werden. Damit ist dann die ganze rechte Seite dieser Gleichung mit 105 multipliziert. Im Bildbereich der Logarithmenrechnung ist das die Addition einer 5 auf der rechten Seite der Gl.2. Das erzeugt dann am Ende einen Logarithmus von 4,00506. Damit das eine Gleichung bleibt, ist ihre linke Seite jetzt als Logarithmus von
). Das ist der Abstand zwischen Standortbreite und Deklination längs eines Meridians. Haben beide das gleiche Vorzeichen, dann wird der Betrag des kleineren Wertes vom Betrag des größeren subtrahiert. Bei ungleichen Vorzeichen werden die Beträge beider Werte addiert. Es fällt auf, dass in der Rechnungsaufstellung von Sumner der mit der eckigen Klammer eingeschlossene Faktor in Gl. 2 mit 105 multipliziert ist, indem die Elemente nat. cos. und nat. sin. mit dem Faktor 105 multipliziert werden. Damit ist dann die ganze rechte Seite dieser Gleichung mit 105 multipliziert. Im Bildbereich der Logarithmenrechnung ist das die Addition einer 5 auf der rechten Seite der Gl.2. Das erzeugt dann am Ende einen Logarithmus von 4,00506. Damit das eine Gleichung bleibt, ist ihre linke Seite jetzt als Logarithmus von ![]() zu verstehen. Aus speziellen Tafeln konnte aus diesem Logarithmus direkt eine sekundengenaue Zeit ausgelesen werden, die in diesem Fall 1:43:59 h lang war. Das ist die Zeit „from noon“, in diesem Fall die Zeit bis zum Mittag, weil die Sonne in der östlichen Hemisphäre beobachtet wurde.
Heute stehen uns derartige Tafeln nicht mehr zur Verfügung.
zu verstehen. Aus speziellen Tafeln konnte aus diesem Logarithmus direkt eine sekundengenaue Zeit ausgelesen werden, die in diesem Fall 1:43:59 h lang war. Das ist die Zeit „from noon“, in diesem Fall die Zeit bis zum Mittag, weil die Sonne in der östlichen Hemisphäre beobachtet wurde.
Heute stehen uns derartige Tafeln nicht mehr zur Verfügung.

Wir verfolgen die Rechnung von Sumner jetzt weiter, nur um sie zu verstehen. Die spezielle Logarithmentafel hat im Prinzip folgende Schritte erledigt:
Jetzt geht es aber weiter, denn aus der Zeit bis Mittag, der Beobachtungszeit und dem Betrag der Zeitgleichung muss die Länge berechnet werden. Dazu wird die Gl 1.2 in der folgenden Aufstellung benutzt und wir erhalten:
Längengrad: ![]()
Das war damals also eine ganz umständliche Rechnerei mit den Zeiten, die mit den vorstehenden ausführlichen Erläuterungen sogar noch komplexer wirkt, als sie wirklich war, denn wir haben heute nicht mehr die damaligen Tafelwerke und müssen mehrere Rechenschritte anwenden, um alles verstehen zu können. Sumner hatte mit seiner Arbeit das Zweihöhenproblem auf eine ganz praktische Art gelöst, nämlich durch grafische Konstruktionen direkt in der Seekarte. Doch auf diese historische Dimension seiner Entdeckung legte er als praktischer Seemann und bescheidener Mensch weniger Gewicht. So schrieb er in der Einleitung zu seinem Buch:
„ Der Zweck dieses Werkes ist weniger, dem Seemann eine neue Methode von „doppelten Höhen“ vorzulegen, als ihm eine genaue Methode zu verschaffen, durch eine Höhe der Sonne, zu irgend einer Stunde des Tages genommen, mit der Chronometerzeit die wahre Richtung des Landes zu finden, wenn die Breite, Länge und Schiffszeit aus irgend einer Ursache ungewiss sind, und ihn aufmerksam zu machen und zu warnen, wenn er nahe einer gefährlichen Küste ist (denn alle Küsten sind gefährlich, wenn die Breite nicht genau bekannt ist), vor jenen Irrtümern der Länge durch den Chronometer, welche aus einer irrtümlichen Breite, die man gebraucht um die wahre Schiffszeit zu finden, entstehen, und besonders seine Aufmerksamkeit auf die Tatsache hinzulenken, dass so wie es in diesen Seiten gezeigt wird, wenn die Breite ungewiss ist, eine einzige Höhe der Sonne zu irgend einer Tageszeit, wenn sie nicht weniger als 7° hoch ist, mit einem guten Chronometer, ebenso nützlich ist, als eine Meridianbeobachtung für die Breite; und die oben angedeuteten Irrtümer werden deutlich gemacht“
Sumner sah, dass ein Standort aus einer gegissten Breite und der Chronometerlänge falsch ist, wenn die angenommene Breite falsch ist und das für Schiff und Mannschaft eine Gefahr bedeutet. Eine Linie aus zwei angenommenen Breiten zeigt jedoch eine wahre Richtung an, wobei die Position des Schiffes irgend ein Punkt dieser Linie ist. Die Breite musste dafür also gar nicht genau bekannt sein. Die neue Art der Positionsangabe war damit eine Linie statt eines Punktes, hatte also einen größeren Informationsgehalt. Außerdem konnte von dieser Linie ein Kurs abgeleitet werden. Bei einem falsch gehenden Chronometer entstand jedoch eine Ost-West Versetzung der Sumnerlinie. Für Sumner hatte eine Standlinie im küstennahen Bereich, wenn die Küste noch unsichtbar war, eine größere praktische Bedeutung als die Bestimmung eines Punktes als Standort. Auf dem offenen Ozean ist ein um ein um mehrere zehn Meilen falscher Punkt-Standort kein Problem. Ganz anders in der Nähe einer Küste. Die Sumner’sche Methode war gewissermaßen ein praktischer Ersatz für die Lösung des Zweihöhenproblems, das vor allen nur noch für Positionsbestimmungen weit draußen auf dem Ozean wichtig war. Ursächlich dafür war nicht zuletzt die noch nicht ganz zufrieden stellende Genauigkeit der Chronometer. Die Bestimmung eines Standortes durch Kreuzung zweier Sumnerlinien soll in einem nachfolgenden Beispiel näher betrachtet werden. Dabei soll ein Taschenrechner zum Einsatz kommen und es wird mit einem modernen Nautischen Jahrbuch gearbeitet. Der Leser kann somit vergleichen und feststellen, dass diese Methode gegenüber der ebenfalls grafischen Hilaire Methode doch einen gewissen Aufwandsvorteil besitzt und gar nicht mal so ungenau ist.
3.2 Folge
Die Sumner Methode markiert den Beginn der sogenannten modernen Astronavigation. In Wirklichkeit bedeutete sie die Abkehr von analytischen Methoden und die Einführung grafischer Methoden. Grafische Lösungen sind Näherungen. Sie unterscheiden sich von analytischen Lösungen vor allem dadurch dass sich die durchzuführenden Berechnungen nicht mehr darauf richten, einen Standort zu berechnen. Bei grafischen Methoden sind Berechnungen nötig, um die Maße der Grafikelemente, wie Winkel, Strecken oder Punkte zu bestimmen, damit daraus eine Zeichnung angefertigt werden kann. Das bedeutet nicht notwendigerweise, dass die Berechnungen dadurch einfacher werden. Doch im 18. Jahrhundert gab es einfach keine Alternative zu grafischen Verfahren. Sie hatten außerdem den großen Vorteil, dass sich die Grafiken direkt auf der Seekarte entfalteten und so ein großes Vertrauen erwecken konnten. Eine lediglich ausgerechnete Zahl für einen Standort, ohne dass dafür eine Karte gebraucht wurde, konnte dagegen kaum Vertrauen erzeugen, zudem diese Zahl auch nur durch Rechnung überprüfbar gewesen wäre. Heute kennt man in der Astronavigation nur das grafische Navigieren nach der Höhendifferenzmethode von Marcq Saint Hilaire, obwohl die Beschränkungen des 19. Jahrhunderts längst verschwunden sind. Doch leider hat das bis heute niemand erkannt.
4 Beispiel einer Sumner Standortbestimmung
Auf dem Weg nach St. Lucia bestimmt ein Segelboot am 5.12.2020 seine Mittagsbreite mit 14°24′ N. Bei einem Kurs von 270° West betrug die Fahrt rund 7 Knoten. Etwa 20 Stunden später, am Vormittag des 6. Dez wurde um 13:08:14 UT1 die Höhe der Sonne mit 35° 32,60’ (berichtigte Höhe) beobachtet. Deklination, Höhe und Greenwichwinkel zu diesem Zeitpunkt betragen:
-
-
- ∂1 = -22° 34,7’ = -22,58°
- h1 = 35° 32,6’ = 35,54°
- Grt1 = 19° 15,2′ = 19,25°
-
Für eine Sumnerlinie müssen zwei Breiten geschätzt werden, zwischen denen man sich befinden sollte. Das ist durch Kopplung an die letzte Mittagsbreiten-Bestimmung kein Problem. Da ständig Westkurs gefahren wurde, sollte die am Vortag gefundene Mittagsbreite zwischen 14° N und 15° N immer noch gelten. Für diese Breiten müssen nur die Längen berechnet werden. Dazu dienen die folgenden beiden Formeln, deren Herleitung im Abschnitt 2 unter Chronometerlänge gezeigt wurde:
![]()
![]()
Weil die Höhe am Vormittag gemessen wurde, muss in den Gleichungen addiert werden. Die Ergebnisse liegen zwischen 0° und 180°. Sie bekommen deshalb ein negatives Vorzeichen oder werden mit W als Westlängen gekennzeichnet. Mit den folgenden Werten kann die erste Sumnerlinie auf einem Stück Papier gezeichnet werden.
-
-
- auf 14° N:
 = -60,44° =060° 26,61′ W
= -60,44° =060° 26,61′ W - auf 15° N:
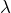 = -59,51° =059° 30,34′ W
= -59,51° =059° 30,34′ W
- auf 14° N:
-
Die beiden Punkte liegen mit 1° Breite weit genug auseinander, so dass die Standlinie problemlos mit einem Lineal eingezeichnet werden kann. Im Bild 4 ist das die grüne gestrichelte Linie. Der eigene momentane Standort ist irgendein Punkt auf dieser Linie. Um 18:25:4 UT1 wird die Sonne nach Gesamtbeschickung mit 37° 6,95’ (berichtigte Höhe) ein zweites Mal beobachtet. Für diese Zeit gelten:
-
-
- ∂2 = -22° 36,23’ = -22,60°
- h2 = 37° 6,95’ = 37,12°
- Grt2 = 98° 26,3′ = 98,44°
-
Es werden dieselben Breiten von 14° N und 15° N gewählt und es wird berechnet, auf welchen Längen diese von der Höhengleiche, die zur angegebenen Zeit mit 37,12° Höhe beobachtet wurde, geschnitten werden. Da die Beobachtung am Schiffsnachmittag erfolgte muss jetzt der Polwinkel vom Greenwichwinkel Grt2 subtrahiert werden. Es gelten jetzt:
![]()
![]()
Auch jetzt liegen die Rechenergebnisse zwischen 0° und 180° und es handelt sich gemäß Gl. 6 um Westlängen. Mit den folgenden Werten kann jetzt die zweite Sumnerlinie eingezeichnet werden. Im Bild 4 ist das die rote Linie.
-
-
- auf 14° N:
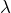 = -59,47° =059° 27,98′ W
= -59,47° =059° 27,98′ W - auf 15° N:
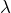 = -60,46° =060° 27,65′ W
= -60,46° =060° 27,65′ W
- auf 14° N:
-
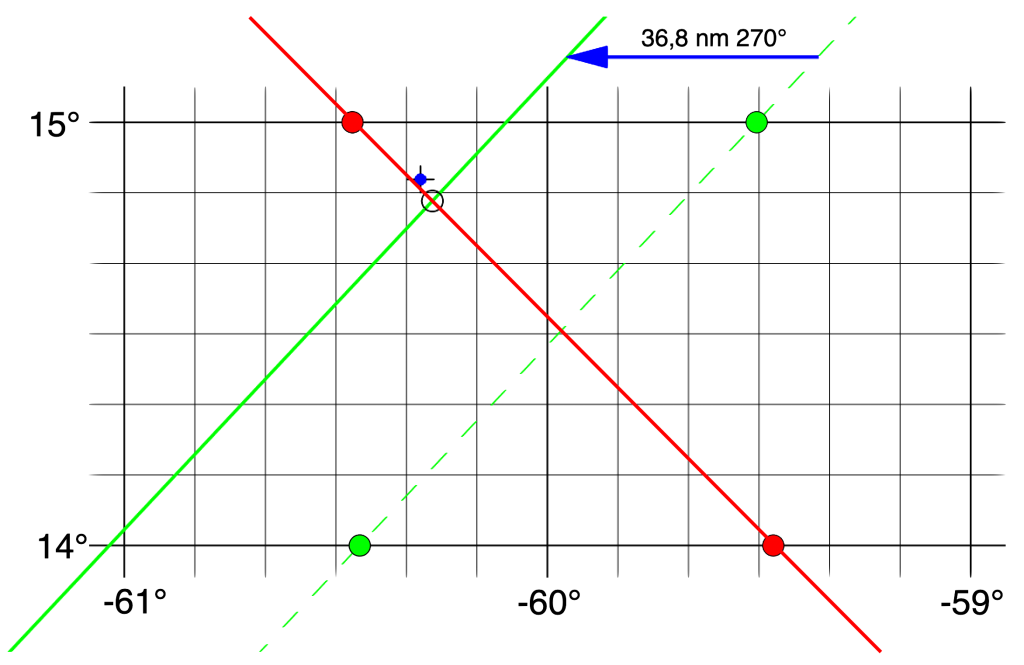
Der Zeitunterschied zwischen den Beobachtungen beträgt etwa 5 Stunden und 17 Minuten. Während dieser Zeit blieb die Geschwindigkeit bei etwa 7 Knoten. Folglich wurde dabei ein Weg von 36,8 nm zurückgelegt, bei einem Kurs von 270°, der ebenfalls nicht geändert wurde. Diese Versegelung muss in der Standortberechnung berücksichtigt werden.
Wir wählen also irgend einen Punkt auf der ersten Standlinie, die in der Grafik grün gestrichelt dargestellt ist und setzen von diesem Punkt in einem Kurs von 270° eine Strecke von 36,8 Seemeilen ab, was auf einem Großkreis genau so viele Bogenminuten wären. Da die Meridiane zu den Polen hin zusammenlaufen, muss diese Strecke vorher mit dem Kosinus der Breite multipliziert werden, was dann 35,55° sind. Um diesen Wert weiter westlich wird nun die versegelte Standlinie als grüne Linie eingezeichnet. Der Standort zum Zeitpunkt der zweiten Beobachtung ist jetzt der Schnittpunkt der verschobenen Standlinie, mit der Standlinie 2, die rot eingezeichnet wurde. Für diesen Schnittpunkt lesen wir aus der Seekarte die folgenden Koordinaten heraus:
Schiffsort nach Sumner: 14° 49’ N 060° 18’ W
Ein Standort nach Sumner ist also auch mit einem Taschenrechner schnell berechnet, etwas Routine vorausgesetzt. Ein Standortfehler kann dadurch entstehen, dass die Messungen von Zeit und Höhe fehlerbehaftet sind. Fehler durch die Methode entstehen dadurch, dass die Breiten 1° auseinanderliegen und dieser Fehler steigt, je kleiner der Durchmesser der Höhengleichen wird. Es ist schließlich auch nur eine Näherungsmethode. Würden die Breiten enger zusammenliegen, z. B. nur eine Bogenminute, dann wären die Sekanten praktisch schon Tangenten und der Systemfehler wäre wesentlich geringer. Doch durch zwei Punkte, die vielleicht nur einem Millimeter auf einer Karte auseinanderliegen, kann niemand mehr eine Gerade im richtigen Winkel durchzeichnen. Die Linien schneiden sich dann irgendwo auf dem Blatt. Hier griff dann 40 Jahre später die Methode von Hilaire, bei der das Azimut berechnet werden musste. Hat man das Azimut, dann hat man auch den Winkel der Standlinie, denn Azimut und Standlinie stehen im rechten Winkel zueinander. Der Schiffsort in diesem Beispiel nach Gauß berechnet ist:
Schiffsort nach Gauß: 14° 50,31’ N 060° 17,78’ W
Die beiden Ergebnisse unterscheiden sich um 1,3 nm in der Breite und 0,2 nm in der Länge, was ein durchaus akzeptables Ergebnis ist. Die Sumner Methode wurde von den damaligen Seefahrern sehr schnell angenommen. Sie erschien sofort logisch, weil sie sich an den Höhengleichen selbst orientierte. Zwei Punkte in der Kreislinie berechnen und diese miteinander zu verbinden ergab zwar eine Gerade. Diese erschien aber angesichts des riesigen Kreisdurchmessers einer Höhengleiche im Standortbereich als ein Stückchen der Kreislinie. Bei der Hilaire Methode stehen die Höhengleichen nicht im Vordergrund. Dort sind es Konstruktionsanweisungen für exakte Standlinien. Das mag vielleicht ein Grund dafür sein, dass ihre praktische Anwendung ohne die erforderliche Routine meist schon nach kurzer Zeit vergessen ist.
Links:
nach oben ♦ Die Sonne am Himmel ♦ Mittagsbreite und Chronometerlänge ♦ Gauß und das Zweihöhenporoblem ♦ Die Methode des Marcq Saint Hilaire ♦ Numerische Standortbestimmung ♦ Navigieren mit Excel ♦ Ein wenig Sextantenkunde ♦ Sextantentest Mark 25 ♦ Downloads ♦ Home
