Darunter wird die Berechnung der Positionen der Bildpunkte aller zur Navigation geeigneter Gestirne verstanden. Diese Daten wurden bis einschließlich 2020 vom BSH in einem nautischen Jahrbuch veröffentlicht. Die Herausgabe des Nautischen Jahrbuches ist inzwischen eingestellt worden, weil es für die Großschifffahrt nicht mehr ausrüstungspflichtig ist. Dieser Beitrag zeigt, wie die Positionen des Bildpunktes der Sonne Grt und ![]() und der Fixsterne berechnet werden.
und der Fixsterne berechnet werden.
Berechnung des Greenwichwinkels der Sonne
Für eine Berechnung muss auf das Kepler Modell zurückgegriffen werden. Das ist ein Zweimassenmodell, welches nur die Massen von Erde und Sonne berücksichtigt und die Massen von Mond und den großen Planeten vernachlässigt. Dadurch entstehen Abweichungen in den Ephemeriden, von bis zu etwa +0,3’ zu den tatsächlichen Daten. Diese Abweichungen sind so klein, dass in einer praktischen Navigation mittlere Fehler von weniger als +5% Standortabweichung zu erwarten sind.
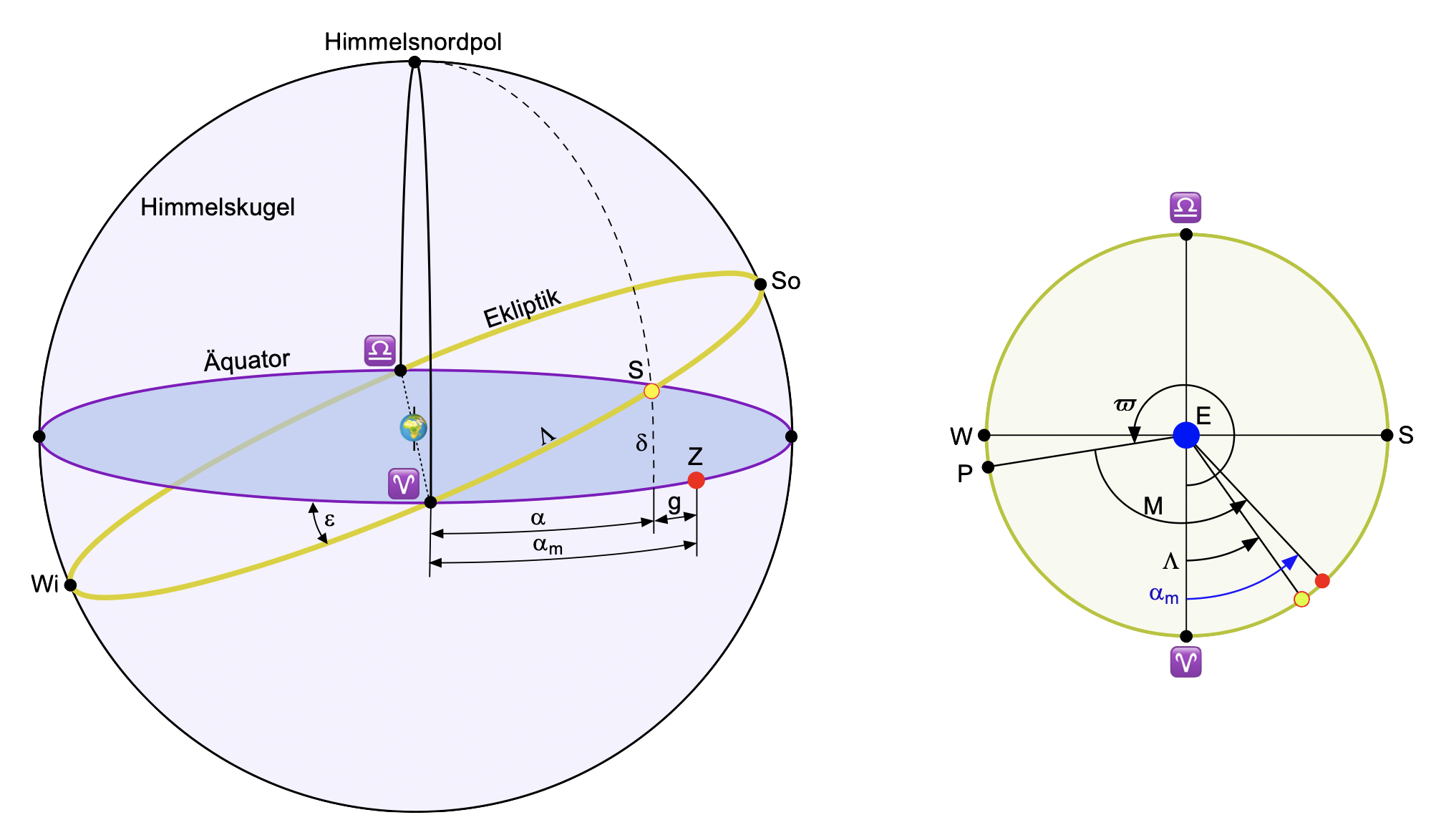
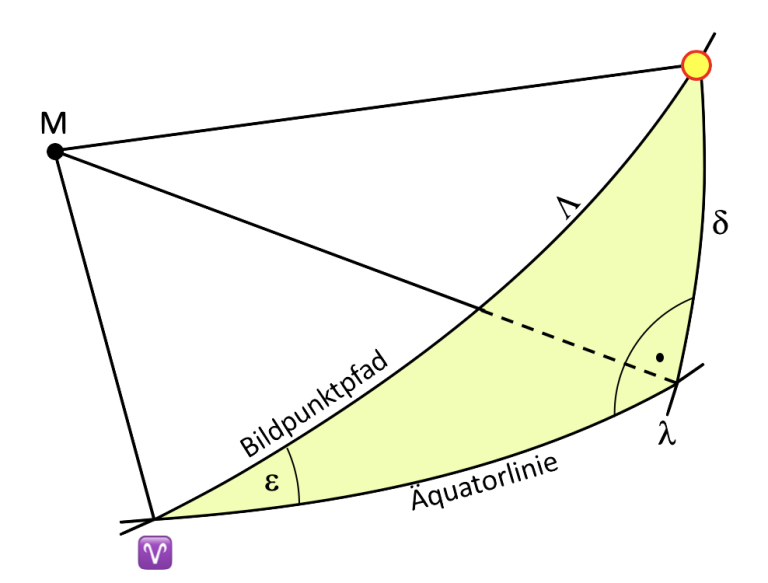
Bild 1 zeigt das zur Berechnung geeignete Modell einer geozentrischen Darstellung. Letztendlich ist es auch egal, von welcher Warte aus die Gesetzmäßigkeiten betrachtet werden. Sie sind immer gleich. Lediglich von der Anschauung her ist es günstig, die Warte zu wechseln und mal ein geozentrisches wie im Bild 1 und ein anderes Mal ein heliozentrisches Modell zu betrachten. Die Darstellung zeigt die Himmelskugel mit der rotierenden Erde im Mittelpunkt. Die Sonne S umrundet die Erde einmal im Jahr auf ihrer ekliptischen Bahn, die zum Himmelsäquator und auch zum Erdäquator die gleiche Schräge von ![]() besitzt mit einer völlig gleichmäßigen Geschwindigkeit.
besitzt mit einer völlig gleichmäßigen Geschwindigkeit.
Vom Frühlingspunkt ausgehend, das ist einer der Schnittpunkte von Himmelsäquator und Ekliptik an der Himmelskugel, bewegt sich die Sonne nordwärts und bescheint die Nordhalbkugel der Erde zunehmend direkter. Dabei erreicht sie als nördlichsten Punkt die Sommersonnenwende So und bewegt sich danach auf ihrer Bahn wieder südwärts. Genau am Herbstanfang, dem zweiten Schnittpunkt von Äquatorebene und Ebene der Ekliptik, passiert der Bildpunkt den Äquator und bewegt sich dann weiter südwärts, wobei die Sonne die Südhalbkugel direkter bestrahlt. Schließlich passiert die Sonne die Wintersonnenwende Wi und erreicht zum Abschluss der Umrundung wieder den Frühlingspunkt.
Auf dem Himmelsäquator soll eine Vergleichssonne Z analog dem Zeiger einer großen Uhr kreisen und zwar mit derselben gleichmäßigen Bahngeschwindigkeit der richtigen Sonne. Außerdem passieren beide Sonnen den Frühlingsanfang und den Herbstanfang im selben Zeitpunkt. Der jeweilige Meridian der Himmelskugel, der durch die echte Sonne verläuft, schneidet den Himmelsäquator im rechten Winkel, wobei dieser Schnittpunkt die Länge ![]() in die Abschnitte
in die Abschnitte ![]() und g teilt. Die Länge g ist dabei die Zeitgleichung.
und g teilt. Die Länge g ist dabei die Zeitgleichung.
Es gibt jedoch ein Problem. Jedesmal, wenn die Sonne nach einem kompletten Umlauf wieder den Frühlingspunkt erreicht, trifft ihr Bildpunkt einen anderen Meridian auf der Erde. Es gibt keine Anzahl von 360° Erdrotationen, die restlos auf einen Umlauf passen, zumal sich die Erde immer langsamer dreht. So beginnt jedes Jahr am 1. Januar 00:00:00 UT auf einem anderen Meridian. Genau deshalb braucht man für jedes Jahr eine neue Tabelle mit der Zeitgleichung oder einen Almanach, der genau nur für ein bestimmtes Jahr gilt. Da muss man fragen, wann die Erde angefangen hat, sich zu drehen, natürlich nur im mathematischen Sinne. Die Antwort ist: am 1. 1. 4713 v. Chr., also vor rund 6000 Jahren. Solange werden die Jahre praktisch sekundengenau bis zum heutigen Tag fortgerechnet. Diese Jahre sind julianische Jahre, benannt nach dem Römischen Kaiser Galius Julius Cäsar.
In dem von ihm geschaffenen julianischen Kalender hatte ein Jahr 365 Tage und jedes vierte Jahr war ein Schaltjahr mit 366 Tagen. Der Kalender hinkte dadurch alle 128 Jahre um einen Tag der auf dem Frühlingsanfang beruhenden astronomischen Realität hinterher. Im Jahr 1582 reformierte Papst Gregor den Kalender, indem 10 Tage einfach übersprungen wurden, denn das Osterdatum war nicht mehr durch Frühlingsanfang und Frühlingsvollmond bestimmt. Auch die Schaltjahresregel wurde geändert, so dass zwar grundsätzlich alle 4 Jahre ein Schalttag hinzukommt, dieser aber auch mal ausfällt oder sogar ein weiterer Schalttag hinzukommt. Den gregorianischen Kalender haben inzwischen die meisten Staaten der Erde übernommen. Doch es bleibt dabei, es wird keinen Kalender geben können, in dem Sonnenjahr und Kalenderjahr übereinstimmen.
Damit nicht immer bis zum Tag null zurückgerechnet werden muss, hat man Etappen festgelegt. Die zuletzt zurückgelegte Etappe endete am 1. Januar 2000 um 12:00:00 UT1. Für dieses Referenzdatum wurden die aktuellen Werte der Bahnelemente der Erde als lineare Gleichungen abgelegt. Die Gleichungen haben alle die Form Y = A + B ⋅ T, wobei A der Wert des Parameters am Referenzdatum ist und das Produkt B ⋅ T die mit den zukünftigen Tagen T zu erwartenden Änderungen beschreibt.

Die Tabelle enthält die am Referenzdatum festgelegten Bahnelemente. Darin bedeuten:
Mittlere Länge in Grad ab Perihel ist die Stelle auf dem Himmelsäquator, die ein dort kreisender Punkt erreicht, wenn er gleichmäßig wie ein Uhrzeiger mit der mittleren Umlaufgeschwindigkeit der Sonne vom Referenzdatum an unterwegs ist.
Länge des Perihel in Grad ist der Punkt auf der Erdumlaufbahn, an dem die Erde im Nordwinter der Sonne am nächsten kommt. Die Länge wird in Grad vom Frühlingspunkt aus gemessen.
Numerische Exzentrizität ist ein Parameter, mit dessen Hilfe ein Kreis in eine Ellipse verwandelt wird, in unserem Fall also ein mathematisches Hilfsmittel, mit dem die elliptische Bahn der Erde um die Sonne festgelegt wird.
Schiefe der Ekliptik in Grad ist der Winkel, den die Ebene der Ekliptik gegenüber der horizontalen Ebene einnimmt. Es ist gleichzeitig der Winkel der maximal möglichen Deklination der Sonne.
Bestimmung der Zeit als Variable
Für eine Navigation werden die Sonnenpositionen Deklination als Abweichung vom Äquator und Stundenwinkel als Längenabstand zu einem festgelegten Nullmeridian gebraucht. Es sollte möglich sein, diese aus den Bahnparametern heraus berechnen zu können. Es muss gelingen, die Position der Sonne, bzw. die Koordinaten ihres Bildpunktes auf der Erdoberfläche, was dasselbe ist, für eine beliebige Chronometer-Sekunde eines beliebigen Jahres im voraus zu berechnen.
Da anders herum ein Navigator aus einer sekundengenau gemessenen Sonnenhöhe über dem Horizont seine Entfernung zum Bildpunkt der Sonne kennt und die Koordinaten des Bildpunktes für diese Sekunde ausgerechnet worden sind, hat er schon mal einen Anhaltspunkt für seine Position. Er befindet sich auf einer Kreislinie mit den Sonnenkoordinaten als Mittelpunkt und dem aus der Sonnenhöhe ermittelten Radius. Dieser Kreis ist der sog. Kreis gleicher Höhe oder Positionskreis. Eine zweite zu einem späteren Zeitpunkt ermittelte Sonnenhöhe ergibt einen zweiten Kreis, der den ersten Kreis überlappt und an zwei Stellen schneiden kann. Einer der dabei entstehenden Schnittpunkte ist dann der Standort. Die Kenntnis der sekundengenauen Sonnenpositionen ist also die Grundlage der Sonnennavigation.
Die vier Bahnparameter in obiger Tabelle beschreiben also die Stellung der Sonne auf der Ekliptik in Bezug zur Erdstellung zu einer Zeit T. Somit besteht die erste Aufgabe darin, diese Zeit als gebrochene Tageszahl auszurechnen. Die Formel dafür lautet:
(1) ![]()
mit
(2) ![]()
Mit ℤ ist der ganzzahlige Teil des Wertes gemeint, der in der nachfolgenden Klammer steht. Beispielsweise ergibt das Jahr 2022 einen Klammerausdruck von 8035,5. Dann ist ℤ = 8035, weil der Nachkomma-Anteil weggelassen wird. Die zu subtrahierende 2000 ist die Jahreszahl des Referenzdatums. Mit N werden die im betrachteten Jahr vergangenen Tage ausschließlich des aktuellen Tages bezeichnet. Somit beträgt N an einem 12. Februar 43 Tage. Die -0,5 Tage sind nötig, wenn der Kulminationszeitpunkt nicht auf 0 Uhr, sondern auf 12 Uhr festgelegt ist. Das ist eine willkürliche Festlegung, die auf der Tradition beruht, dass 12 Uhr die Mittagszeit ist und die Sonne am Mittag ihren höchsten Stand hat. Der nachfolgenden Bruch UT1/24 legt den gebrochenen Tagesanteil fest. Mit SJ ist die mit Gl. 2 beschriebene Schaltjahresregel gemeint, die bis 2099 gilt. Ein Schaltjahr gibt es immer dann, wenn die Jahreszahl ohne Rest durch 4 teilbar ist. Gelesen wird diese Gleichung als: Wenn 4 der Teiler von (JJJJ – 2000) ist, dann 1, wenn nicht, dann 0. Somit ist jedes vierte Jahr ein Schaltjahr, in dem dann ein Tag abgezogen werden muss. Subtrahieren ist deshalb angebracht, weil der Nachkommawert von 0,25 bei der Multiplikation mit 365,25 alle vier Jahre einen zusätzlichen Tag hervorbringt. An den Jahrhundertwenden fallen Schaltjahre aus, weshalb die Regelung mit der Gl. 3 nur bis ins Jahr 2099 gilt. Das Jahr 2100 ist zwar durch 4 teilbar, aber auch durch 100 und fällt deshalb als Schaltjahr aus.
Zur Zeitmessung verwenden die Menschen Räderuhren, die sehr gleichmäßig laufen. Der von diesen Uhren angezeigte Lauf der Zeit ist mit dem Lauf der Vergleichssonne Z im Bild 1 vergleichbar, deren Bildpunkt den Äquator nie verläßt, aber pro Zeiteinheit immer die gleiche Längengraddifferenz zurücklegt. Das ist bei der echten Sonne nicht so. Sie legt pro Zeiteinheit immer eine andere Längengraddifferenz zurück. Nehmen wir ihre Geschwindigkeit auf der Umlaufbahn konstant an, dann überschreitet ihr Bildpunkt in derselben Zeit mehr Meridiane, wenn ihr die Nord- oder Südhalbkugel zugewandt ist, als wenn ihr der Äquator zugewandt ist, wo die Meridiane am weitesten auseinanderliegen. Der Längengrad, auf dem sich der Bildpunkt der wahren Sonne gerade befindet unterscheidet sich von dem Längengrad, auf dem sich der Bildpunkt der Vergleichssonne befindet um den im Bild 1 gezeigten Betrag g. Dieser Längengrad Unterschied ist die Zeitgleichung, weil 1° Längendifferenz dasselbe ist wie 4 Minuten Sonnenlaufzeit. Wenn es also darum geht, die Bildpunktlänge der wahren Sonne mit der Zeitangabe eine Räderuhr festzustellen, dann ist deren Zeitangabe eine mittlere Zeit und die wahre Sonnenzeit erhält man erst durch Addition der Zeitgleichung. Früheren Navigatoren stand für jedes Jahr die Zeitgleichung in Form einer Tabelle zur Verfügung, wie sie nachstehend als Ausschnitt gezeigt wird.
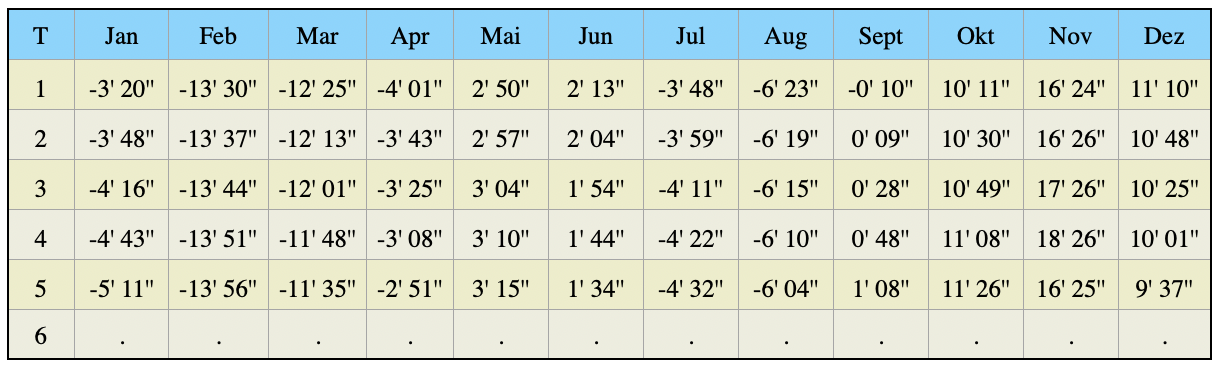
Ein Navigator ermittelte den Stundenwinkel der Sonne nach der von einem Chronometer angezeigten Zeit, die er mit der Zeitgleichung korrigieren musste. War die Differenz des Korrekturbetrages von einem auf den anderen Tag zu groß, dann musste sie sogar auf die Stunde der Beobachtung umgerechnet werden. Später wurde der Aufwand dieser Umrechnung dadurch behoben, dass Tabellen herausgegeben wurden, in denen für jeden Tag der Stundenwinkel im Stundenraster angegeben wurde. Das waren dann die Nautischen Jahrbücher.
Berechnung der Zeitgleichung
Nach Bild 5 ist die Zeitgleichung einfach die Auflösung folgender Beziehung:
(3) ![]()
Unter ![]() versteht man den Hauptwinkel der Länge L. So hat die Erde beispielsweise im Juli 2021 ihre Bahn um die Sonne schon etwa etwa 21,5-mal mit je 360° ausgeführt und das wären dann knapp 21,5 ⋅ 360° = 7740° plus die 280° vom Frühlingspunkt bis zum Perihel. Insgesamt wären das dann 8020°. Die genaue Zahl liefert das Bahnelement L. Den Hauptwinkel erhält man dadurch, dass volle 360° Umrundungen aus der Zahl herausgenommen werden. Dafür gilt dann die folgende Formel:
versteht man den Hauptwinkel der Länge L. So hat die Erde beispielsweise im Juli 2021 ihre Bahn um die Sonne schon etwa etwa 21,5-mal mit je 360° ausgeführt und das wären dann knapp 21,5 ⋅ 360° = 7740° plus die 280° vom Frühlingspunkt bis zum Perihel. Insgesamt wären das dann 8020°. Die genaue Zahl liefert das Bahnelement L. Den Hauptwinkel erhält man dadurch, dass volle 360° Umrundungen aus der Zahl herausgenommen werden. Dafür gilt dann die folgende Formel:
(4) 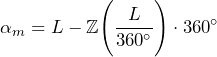
Mit der Berechnung von ![]() wird es dann schon komplizierter. Wie Bild 5 zeigt, bilden
wird es dann schon komplizierter. Wie Bild 5 zeigt, bilden ![]() ,
, ![]() und
und ![]() , alles sind Großkreisabschnitte, ein rechtwinkliges Kugeldreieck mit dem rechten Winkel zwischen
, alles sind Großkreisabschnitte, ein rechtwinkliges Kugeldreieck mit dem rechten Winkel zwischen ![]() und dem durch die Sonne gehenden Meridian. Für dieses Dreieck ist die Berechnungsformel in einem Formelbuch mit
und dem durch die Sonne gehenden Meridian. Für dieses Dreieck ist die Berechnungsformel in einem Formelbuch mit ![]() schnell gefunden. Unter Berücksichtigung der Vollkreisigkeit ist es jedoch günstiger, mit der Transformationsformel
schnell gefunden. Unter Berücksichtigung der Vollkreisigkeit ist es jedoch günstiger, mit der Transformationsformel
(5) ![]()
zu arbeiten. Man hätte sonst mit zu vielen Überläufen zu tun. Der Index ![]() in der Arcusfunktion ruft den Winkel auf, der
in der Arcusfunktion ruft den Winkel auf, der ![]() am nächsten liegt. Diese Formel ist dann folgendermaßen zu verwenden:
am nächsten liegt. Diese Formel ist dann folgendermaßen zu verwenden:
(6) 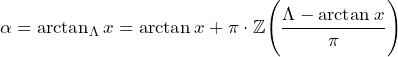
Darin ist ![]() . Um die Gleichung lösen zu können, wird
. Um die Gleichung lösen zu können, wird ![]() gebraucht und dafür gilt:
gebraucht und dafür gilt:
(7) ![]()
Mit C kommt hier die sogenannte Mittelpunktsgleichung ins Spiel und die dient zur Berechnung einer elliptischen Bahn durch elliptische Verformung einer Kreisbahn. Sie hängt nach Kepler von der Exzentrizität e der jeweiligen Bahnellipse ab und ist die Differenz zwischen mittlerer Anomalie M und wahrer Anomalie V. Das soll an dieser Stelle aber nicht weiter vertieft werden. Die mittlere Anomalie ist die Differenz aus mittlerer Länge und Länge des Perihels. Dafür gilt:
(8) ![]()
Mit den 360° wird nur die Grafik von Bild 5 rechts deutlicher. Dieser Vollkreiswinkel spielt mathematisch jedoch keine Rolle, da im Weiteren nur der Sinus von M benutzt wird und da ist es völlig gleich, wie oft 360° noch dazu addiert werden. Selbst die Formel M = L – ϖ würde dasselbe Ergebnis liefern, das nur grafisch nicht so einfach wiedergegeben werden könnte. Da die Kepler Gleichung nur iterativ zu lösen ist und die Exzentrizität der Erdbahn mit e = 0,0167 recht klein ist, ist hier eine Reihenentwicklung sinnvoller. In der Literatur findet man dafür:
(9) 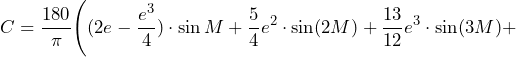
![Rendered by QuickLaTeX.com \[\frac{103}{96}e^4\cdot\sin 4M+\frac{1097}{960}e^5\cdot\sin (5M)\Bigg)\]](https://zephir-yacht.com/wp-content/ql-cache/quicklatex.com-3c5313d0cf92762560afaf2bb6fdcda5_l3.png)
Die zweite Zeile dieser Gleichung, die letzten beiden Summen in der Klammer kann man auch getrost weglassen. Sie bringen keinen Beitrag mehr zum Ergebnis. Mit dem Ergebnis kann jetzt ![]() nach Gl. 7 berechnet werden und liefert nach Ausrechnen der Gl. 5 unter Benutzung der Lösungshilfe in Gl. 6 die Länge
nach Gl. 7 berechnet werden und liefert nach Ausrechnen der Gl. 5 unter Benutzung der Lösungshilfe in Gl. 6 die Länge ![]() . Damit läßt sich dann mit Gl. 3 die Zeitgleichung in Grad angeben. Eine Multiplikation mit 4 liefert das Ergebnis auch in Minuten, wie es z. B. mit der Tabelle 2 angegeben wird.
. Damit läßt sich dann mit Gl. 3 die Zeitgleichung in Grad angeben. Eine Multiplikation mit 4 liefert das Ergebnis auch in Minuten, wie es z. B. mit der Tabelle 2 angegeben wird.
Die Zeitgleichung ist wie bereits beschrieben von der Exzentrizität und von der Ekliptikschiefe, also von zwei Komponenten abhängig. Der Beitrag aus der Bahnexzentrizität wird dadurch berechnet, dass Ekliptikachse und Erdachse parallel gestellt werden. Dafür gilt:
(10) ![]()
Dieser Teil verläuft Teil sinusähnlich mit einer Periode in einem Jahr. Es ist die grüne Strich-Punkt Kurve im Bild 6 und ergibt sich ebenfalls aus der Gl. 7 durch Umstellung auf ![]() als -C.
als -C.
Die zweite Komponente ist der Beitrag, der auf die Schiefe der Ekliptik zurückzuführen ist und ergibt sich als
(11) ![]()
Die Anwendung des Arcustangens mit Lageparameter gemäß Gl. 6 verhindert nicht, dass hier Zahlenwerte auftreten, die über die Erwartungen hinausgehen. Erwartet werden jedoch Werte, die über 0,07, das entspricht 4° keinesfalls hinausgehen. Sollten Zahlen größer als dieser maximal zu erwartende Wert errechnet werden, dann muss vom Ergebnis der Gleichung ![]() subtrahiert werden. Der Verlauf ist, wie oben bereits erwähnt, ebenfalls sinusförmig, jedoch mit zwei Perioden in einem Jahr und ist im Bild 6 als rot gestrichelte Kurve dargestellt.
subtrahiert werden. Der Verlauf ist, wie oben bereits erwähnt, ebenfalls sinusförmig, jedoch mit zwei Perioden in einem Jahr und ist im Bild 6 als rot gestrichelte Kurve dargestellt.
Die Zeitgleichung ist die Summe der mit den Gleichungen 10 und 11 beschriebenen Komponenten und somit
(12) ![]()
Das Ergebnis ist, wie zu erwarten, die Gl. 3 und im Bild 6 die durchgehend schwarze Kurve.
Wenn die Zeitgleichungskomponenten nicht einzeln berechnet werden sollen, sondern die Zeitgleichung direkt, was für eine praktische Verwendung ausreicht, dann hilft die nachfolgend beschriebene Umformung. Durch Ersetzen von ![]() in Gl. 12 bzw. 3 durch Gl. 5 kann die Zeitgleichung auch ausführlicher angegeben werden:
in Gl. 12 bzw. 3 durch Gl. 5 kann die Zeitgleichung auch ausführlicher angegeben werden:
![]()
Ein Tangens Additionstheorem lautet:
![]()
Die Tangens-Umkehrfunktion liefert dafür:
![]()
Mit x = ![]() und
und ![]() folgt daraus:
folgt daraus:
(13) ![]()
Alle bisher angegebenen Gleichungen liefern Winkeldaten und diese sogar fast immer im Bogenmass, als Radiant. Die entsprechenden Zeitangaben erhält man daraus nach Multiplikation mit 4 Min/Grad.
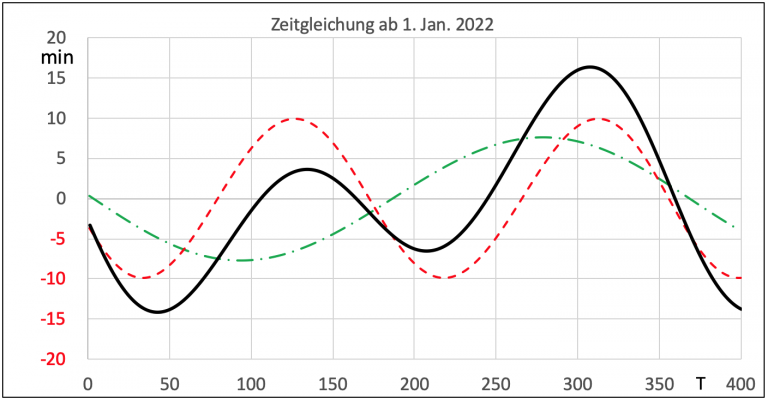
Extrema: 11. Februar, 14. Mai, 26. Juni, 3. September
Bild 2 Zeigt die Verlaufe der Zeitgleichung ab dem 1. Januar des Jahres 2022. Die beiden Komponenten sind farbig dargestellt. Die grün unterbrochene Linie entsteht aufgrund der Elliptizität der Erdumlaufbahn gemäß der Gl. 10 und die rot unterbrochene Linie ist die Folge der Schiefe der Ekliptik gemäß der Gl. 11. Durch Addition der Funktionswerte erhält man die zusammengefasste Zeitgleichung, die als schwarze Kurve gemäß den Gln. 12 und 13 dargestellt ist. An den vier Nulldurchgängen dieser Kurve ist zu erkennen, dass die wahre Sonnenzeit nur an vier Daten im Jahr mit der Zeit einer Räderuhr übereinstimmt und sonst bis zu einer viertel Sunde vor- oder nachlaufen kann. Die Kenntnis der Zeitgleichung ist unverzichtbar für eine Standortbestimmung auf hoher See.
Das nautische Jahrbuch
Ab dem Beginn des 19. Jahrhunderts entwickelte sich die Bestimmung des Längengrades mittels Chronometer und Zeitgleichung mit steigender Anzahl von Schiffschronometern langsam zur gängigen Praxis. Die Einteilung des Gradnetzes der Erde in 180 positive Ostgrade und 180 negative Westgrade passt leider nicht optimal zum Lauf der Sonne. Man brauchte einen Stundenwinkel, der mit dem Lauf der Sonne nach Westen zählt und von 0° bis 360° die Erde umrundet, während die Uhr parallel dazu ihre 24 Stunden abdreht. Dabei ist nur hinderlich, dass der Beginn der Zeitzählung dieser 24 h nur viermal im Jahr mit dem Beginn der Gradzählung am Nullmeridian zusammenfällt. Addiert man jedoch den jeweiligen Tagesbetrag der Zeitgleichung zur Zeitangabe einer Räderuhr, dann ist beides fast wieder synchron, d. h., die Gradzählung am Nullmeridian beginnt mit 12:00:00 UT1 und endet nach 24 Stunden und 360° wieder an derselben Stelle. Eine stundenweise Veränderung der Zeitgleichung wurde hier nicht berücksichtigtg.
Zur Berechnung des Längengrades, auf dem sich der Bildpunkt der Sonne zu einem bestimmten Zeitpunkt des Jahres gerade befindet, brauchte man ein Chronometer und eine Tabelle mit der Zeitgleichung. Ein Beispiel soll aufzeigen, wie das anfangs grundsätzlich gemacht wurde. Gesucht wird die Länge des Bildpunktes der Sonne am 20, August 2022 um 14:00 UT. Dafür wäre dann zu rechnen:
-
- Zeitgleichung am 20. Aug. 12:00: -3’ 24’’
- Zeitgleichung am 21. Aug. 12,00: -3’ 10’’
- Differenz von Tag zu Tag steigend: ↑ 14,7’’/24 h = ↑1,2’’2/h
- Zielstunde = 2 h nach Mittag: 2:00:00 GMT
- plus Zeitgleichung des Tages: -0:03:24
- plus Anteil der 2 h nach dem Mittag: 0:00:01
- wahre Sonnenzeit: 2:56:37 GMT → 29° 9,3’ W
Die Chronometerzeit von 14:00 UT ist eine mittlere Zeit, zwei Stunden nach Mittag, und würde einer Länge von 30° W entsprechen. Mit dem Stand der Sonne kann die Länge aber nur unter Benutzung der wahren Sonnenzeit ermittelt werden und die erhält man erst nach Addition der Zeitgleichung des entsprechenden Tages. Für das Beispiel entnimmt man der Zeitgleichungstabelle für den 20. Aug. 2022 12:00 UT g = -3’ 24’’. Da der Zeitgleichungsbetrag zum Folgetag hin mit 14,7 s ansteigt ↑, entfallen auf die 2 Stunden nach dem Mittag 14,7 ⋅ 2/ 24 rund 1 Sekunde. Als Ergebnis errechnet sich daraus eine Länge von 29° 9,3’ W, auf der sich der Bildpunkt der Sonne befindet.
Diese Rechnerei ist nicht kompliziert, birgt aber die Gefahr, dass man sich verrechnen kann und sie bläht die ohnehin schon komplexen Standortberechnungen nur unnötig auf, weil sie für jede Beobachtung erforderlich ist. Außerdem sind die Ergebnisse nicht sehr genau, weil nur immer auf volle Sekunden gerundet wird. Würde man in diesem Beispiel mit Dezimalsekunden rechnen, dann käme eine Länge von 29° 9,2’ heraus.
Besser ist es deshalb, den Stundenwinkel in Abhängigkeit von der Sonnenzeit zu tabellieren. Dazu müsste die zuvor ausgeführte Berechnung für jede Stunde eines Jahres ausgeführt werden. Das Ergebnis ist dann der sogenannte Sun Almanac, der Teil eines jeden Nautischen Jahrbuches ist. Die nachstehende Tabelle zeigt, den prinzipiellen Aufbau eines Sun Almanac am Beispiel einiger Stunden am 20. August 2022. Der Sinn der vorstehenden Rechnung ist darin für jede Stunde ausgeführt und braucht deshalb vom Navigator nicht mehr gemacht werden. Die erste Spalte enthält die Tageszeit und die beiden nächsten Spalten den Greenwichwinkel Grt, der als Stundenwinkel der Sonne auf den Nullmeridian durch die Sternwarte von Greenwich berechnet ist. Zwei weitere Spalten enthalten dann auch noch die Deklination, also die geografische Breite, auf der sich der Bildpunkt in der links angegebenen Stunde gerade befindet. Man kann sehen, dass der Bildpunkt der Sonne um 12:00:00 UT1 noch 0,852° östlich von Greenwich liegt und diesen Ort erst in 3 Minuten und 24 Sekunden erreichen wird. Daraus folgt dann die Transitzeit, die in einem Nautischen Jahrbuch auch immer unterhalb der Grt Spalte angegeben ist und sie beträgt an diesem Tag 12:3:24.

Ein Nautisches Jahrbuch ist allerdings sehr viel umfangreicher angelegt. Es besitzt für jeden Tag des Jahres eine sog. Tagseite. Darauf werden die Gestirnspositionen als Greenwich Stundenwinkel Grt und die Deklination ![]() im Stundenraster für die Sonne, den Mond und die vier navigationstauglichen Planeten angegeben. Für die Navigation mit Fixsternen wird der ♈︎Grt benötigt, das ist der Grt des Fühlingspunktes. Wird dieser zum mit
im Stundenraster für die Sonne, den Mond und die vier navigationstauglichen Planeten angegeben. Für die Navigation mit Fixsternen wird der ♈︎Grt benötigt, das ist der Grt des Fühlingspunktes. Wird dieser zum mit ![]() angegebenen Sternwinkel eines Fixsterns addiert, dann erhält man den Grt des Fixsterns. Allerdings sind die Positionen eines Fixsterns gar nicht so fix, wie man früher einmal dachte und so muss auch der Sternwinkel einiger Fixsterne von Jahr zu Jahr neu angegeben werden.
angegebenen Sternwinkel eines Fixsterns addiert, dann erhält man den Grt des Fixsterns. Allerdings sind die Positionen eines Fixsterns gar nicht so fix, wie man früher einmal dachte und so muss auch der Sternwinkel einiger Fixsterne von Jahr zu Jahr neu angegeben werden.
Ein nautisches Jahrbuch enthält aber noch mehr. Weil die Stundenwinkel nur im Stundenraster angegeben sind muss auf die Minuten und Sekunden einer Beobachtungszeit interpoliert werden. Dafür stehen am Ende des Buches sogenannte Schalttafeln zur Verfügung, damit auch hier nicht gerechnet werden muss. Wichtig sind auch die Tabellen für eine Sextantenbeschickung. Darüber hinaus wird immer noch die Zeitgleichungstabelle des Jahres angegeben, weiterhin die Fehlerkorrekturen für die Nordsternbreite und vieles andere mehr.
Die erste deutsche Ausgabe eines Nautischen Jahrbuchs gab es für das Jahr 1852 vom Deutschen Hydrographischen Institut in Hamburg. Die Bezeichnung dieses Amtes wechselte später in Bundesamt für Seeschifffahrt und Hydrographie (BSH). Die letzte Ausgabe gab es für das Jahr 2020, womit eine alte Tradition endete. Die Seeschifffahrt benutzt heute nur noch die vollelektronische Satellitennavigation. Unterlagen für eine astronomische Navigation sind in der Seeschifffahrt nicht mehr ausrüstungspflichtig. Wer darauf noch Wert legt, z. B. aus Sicherheitsgründen oder weil er Astronavigation als Hobby betreiben möchte, der kann sich die entsprechenden Tabellen aus dem Internet beschaffen. Eine andere Möglichkeit besteht darin, die Ephemeriden für die Sonne und die Fixsterne mit ausreichender Genauigkeit auf einem PC selbst zu berechnen.
Berechnung der Greenwich Stundenwinkel
Der Greenwich Stundenwinkel Grt, in der angelsächsischen Literatur bezeichnet man ihn mit GHA (Greenwich Hour Angle), wird nicht mit Hilfe einer Zeitgleichungstabelle berechnet, wie das in dem vorstehenden Beispiel gezeigt wurde, sondern direkt unter Verwendung der Gl. 13. Das Koordinatensystem der Erde reicht von -180 bis +180°. Beide Winkel treffen sich an der Datumsgrenze. Genau in der Mitte dazwischen liegt dann mit 0° der durch Greenwich laufende Nullmeridian. Der Greenwichwinkel folgt dem Lauf des Bildpunktes der Sonne. Sein Betrag startet mit null am Nullmeridian und umrundet die 360° des Erdballs. Da die Tageszeit bei 180° E beginnt, der Nullmeridian aber 180° weiter westwärts liegt, muss dieser Versatz mit 12h berücksichtigt werden. Die Formel dafür lautet:
(14) ![]()
Hierin ist t die Zeit UT1 des Tages im 24 Stunden Lauf, für die der Grt berechnet werden soll. Die Zeit 12h ist die Zeit, die von der Sonne gebraucht wird, um von 180° E bis zum Nullmeridian zu kommen. Der Ausdruck ![]() besagt, dass der Klammerinhalt nicht größer als 24 h sein darf. Bei Nachmittags Beobachtungen müssen deshalb immer 24 Stunden subtrahiert werden. Mit 15 ist die Winkelgeschwindigkeit der Sonne von 15°/h gemeint und g ist die in Grad angegebene Zeitgleichung gemäß Gl. 13.
besagt, dass der Klammerinhalt nicht größer als 24 h sein darf. Bei Nachmittags Beobachtungen müssen deshalb immer 24 Stunden subtrahiert werden. Mit 15 ist die Winkelgeschwindigkeit der Sonne von 15°/h gemeint und g ist die in Grad angegebene Zeitgleichung gemäß Gl. 13.
Greenwich Stundenwinkel von Fixsternen
Nur der Vollständigkeit halber soll auch noch auf den ♈︎Grt eingegangen werden, der zur Navigation mit Fixsternen gebraucht wird. Insbesondere soll dabei interessieren, wie dieser aus der Zeit UT1 berechnet wird, denn unsere Uhren geben UT1 an und nicht die Sternzeit. Anders gesagt, wir wollen den Grt eines Sterns zu einer in UT1 gemessenen Beobachtungszeit aus dem Jahrbuch herauslesen können und nicht in Sternzeit. Sternzeituhren gibt es in Sternwarten, aber nicht auf Segelschiffen. Dazu benötigt man für jeden Tag die Sternzeit in Greenwich um 0h UT1. Ihre Berechnung wurde von den Astronomen festgelegt als
(15) ![]()
(16) 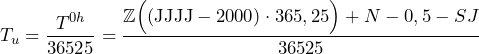
Hierin ist T die Anzahl der seit dem 1. Januar 2000 verstrichenen Tage gemäß der Gl. 1 und der Schaltjahresregel gemäß Gl. 2. Bleiben wir beim 20. August des Jahres 2022, dann erhalten wir für die Greenwich-Meridian-Sternzeit um 00:00:00 UT1 einen Betrag von GMST0h = 1979595,502 Sekunden und das sind 549,888 Stunden. Diese Zeit erhöht sich mit jedem Umlauf der Erde um die Sonne um 24 Stunden, was die Summe der täglichen Nachdrehzeiten der Erde von etwa 4 Minuten über den Zeitraum genau eines Jahres ist.
Um die Sternzeit GMST für einen beliebigen Zeitpunkt UT1 eines gegebenen Tagesdatums bestimmen zu können, muss man UT1 in jeder Zeile mit 1,00273790935 (= Synodische Tageslänge/Siderische Tageslänge) multiplizieren und dazu die Sternzeit GMST0h der Stunde 0 des Tages gemäß der Gl. 15 addieren. Das hört sich etwas kompliziert an, ist aber nötig, um ♈︎Grt angeben zu können. Die so erhaltenen Zeiten mit 15°/h multipliziert, liefern dann den ♈︎Grt des Frühlingspunktes. Betrachten wir hierzu wieder unser Beispiel mit 11:00 UT1:
-
- GMST0h am 20. Aug. 2022: 549,888 h
- 11h, UT1 ⋅ 1,00273790935: 11,030 h
- Summe: 560,918 h
- Verkürzen: 8,918 h
- Stundenwinkel: 8,918 h ⋅ 15°/h = 133° 45,98’
Verkürzen bedeutet, dass 24 h so oft aus der Summe entfernt werden müssen, bis ein Zeitrest von weniger als 24 h übrig ist. Dieser Zeitrest mit 15°/h multipliziert ist dann der Stundenwinkel des Frühlingspunktes ♈︎Grt = 133,763° bzw. 133° 45,75’. Die nachstehende Tabelle zeigt die entsprechende Darstellung in einem nautischen Jahrbuch und gibt auch Sternwinkel sowie Deklination einiger Fixsterne an.
Damit kann jetzt der Grt eines Fixsterns bestimmt werden, indem Greenwichwinkel ♈︎Grt des Frühlingspunktes und Sternwinkel ![]() des betreffenden Sterns addiert werden. Beispielsweise erhalten wir für den Stern Aldebaran am 20.8.2022 um 14:00 UT1:
des betreffenden Sterns addiert werden. Beispielsweise erhalten wir für den Stern Aldebaran am 20.8.2022 um 14:00 UT1:
-
-
-
-
-
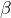 = 290° 42,0’
= 290° 42,0’ - ♈︎Grt = 178° 53,4’
- Grt = 468° 95,4’ = 109° 35,4’
-
-
-
-
Allerdings ist der Aldebaran um 14:00 UT1 auf seiner Länge nicht sichtbar, es sollte auch nur gezeigt werden, wie der grundsätzliche Rechenablauf ist.
Berechnung der Deklination
Die ersten Deklinationstabellen existierten bereits im Mittelalter. Man stellte sich ihren Verlauf als Sinuswelle vor, die an den Tagundnachtgleichen ihren Nulldurchgang hatte und an den Sonnenwenden ihren jeweiligen Maximalwert von 23,44°. Diese Näherung kam auch etwa so hin. Die tatsächliche Deklination ist einfach auszurechnen, weil ein rechtwinkliges Kugeldreieck vorliegt, das aus den Seiten ![]() ,
, ![]() und der Äquatorlinie
und der Äquatorlinie ![]() im Bild 1 besteht. Der rechte Winkel besteht zwischen den Seiten
im Bild 1 besteht. Der rechte Winkel besteht zwischen den Seiten ![]() und
und ![]() Die Berechnungsformel dafür lautet:
Die Berechnungsformel dafür lautet:
(17) ![]()
Die Gl. 7 liefert hierfür die Länge ![]() und mit dem Quotienten 180°/
und mit dem Quotienten 180°/![]() wird der Winkel in Grad berechnet. Nach Berechnung der Zeitgleichung mit Gl.13 und ihrer Anwendung mit Gl. 14 Sowie der Berechnung der Deklination gemäß Gl. 17 ist es nun recht einfach, einen „Sun Almanac“ für ein beliebiges Jahr in diesem Jahrhundert zu berechnen.
wird der Winkel in Grad berechnet. Nach Berechnung der Zeitgleichung mit Gl.13 und ihrer Anwendung mit Gl. 14 Sowie der Berechnung der Deklination gemäß Gl. 17 ist es nun recht einfach, einen „Sun Almanac“ für ein beliebiges Jahr in diesem Jahrhundert zu berechnen.
Wie die Berechnung von Grt und ![]() ganz einfach für eine beliebige Zeit, bestehend aus Datum und Sekunde eines Tages, mit einer Excel Tabelle erfolgt, wird in dem Beitrag Navigationsprogramm mit Excel selbst gemacht beschrieben. Ein Excel Sheet mit einer Tagesseite zum Ausdrucken enthält die Excel Datei hundertjährige Ephemeriden.
ganz einfach für eine beliebige Zeit, bestehend aus Datum und Sekunde eines Tages, mit einer Excel Tabelle erfolgt, wird in dem Beitrag Navigationsprogramm mit Excel selbst gemacht beschrieben. Ein Excel Sheet mit einer Tagesseite zum Ausdrucken enthält die Excel Datei hundertjährige Ephemeriden.