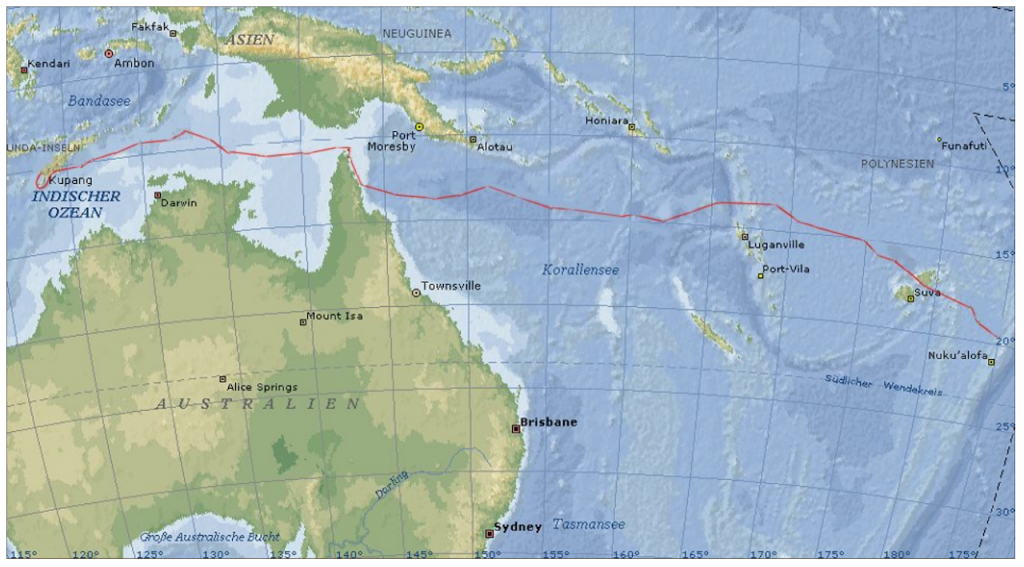
28. April 1789, die berühmteste Seereise der Welt. Captain Bligh von der Bounty kehrt nach 4000 sm in einer kleinen Barkasse in die Zivilisation zurück.
Der Beitrag behandelt einen Teil der sogenannten alten Methoden der Astronavigation. Es ist eine Einführung in ein Thema, das in früheren Jahrhunderten noch als Geheimwissenschaft gehandelt wurde. Ziel einer Standortbestimmung ist das Finden des Breiten- und Längengrades des eigenen Standortes. So hat James Cook im 18. Jahrhundert navigiert und die Küsten von Australien und Neuseeland erstaunlich genau vermessen. Erforderliche Hilfsmittel sind ein Chronometer (Quarzuhr), ein Sextant und das Nautische Jahrbuch. Ein Chronometer stand James Cook allerdings erst auf seiner zweiten Reise zur Verfügung. Bis dahin mußte er sich mit komplizierten Berechnungen auf der Grundlage von Monddistanzen zu bekannten Fixsternen herumschlagen, um die jeweilige Zeit am Greenwich Nullmeridian bestimmen zu können.
Die alten Methoden wurden in der zweiten Hälfte des 19. Jahrhunderts durch die sogenannte moderne Astronavigation abgelöst. Die zeichnet sich dadurch aus, dass Länge und Breite eines Standortes gleichzeitig und zu beliebigen Tageszeiten bestimmt werden konnten. Schon viel früher, im Jahre 1812, waren die mathematischen Grundlagen für eine ideale Form der Astronavigation gelegt worden. Aufgrund verschiedener Umstände wurde davon aber nie Gebrauch gemacht.
1 Nordsternbreite und Mittagsbreite
Die Bestimmung der Breite gehört zu den ältesten Navigationsverfahren überhaupt. Als das Längenproblem noch nicht gelöst war hatten die Seeleute nur eine Chance ihr Ziel zu finden indem sie auf einem bekannten Breitenkreis nach Osten oder Westen segelten. Sie breitelten sich über die Meere und wechselten die Breite je nach Erfordernis. Doch wie bestimmten Sie die Breite?
Wie der Beitrag “Die Sonne am Himmel” zeigt, ist der Winkel zwischen Gestirn und Zenit gleich der Entfernung zum Bildpunkt des Gestirns. Da man zum Zenit nicht messen kann, weil es da keine Markierung gibt, mißt man die Höhe zwischen Gestirn und Kimm und zieht diesen Wert von 90° ab. Das Ergebnis ist dann die Entfernung zum Bildpunkt in Grad. Will man die Entfernung in Meilen haben, dann ist dieser Gradwert mit 60 zu multiplizieren, denn 1 Grad sind 60 Seemeilen. Wenn ein Gestirn genau im Süden oder genau im Norden beobachtet werden kann, dann befindet sich der eigene Standort auf genau demselben Meridian wie der Bildpunkt des Gestirns. Zur Bestimmung der Breite muss dann nur die Entfernung zum Bildpunkt gemessen und mit der Deklination des Gestirns verrechnet werden.

Vor dem Sextanten war der Jakobsstab das gebräuchlichste Gerät zur Bestimmung der Gestirnshöhe über dem Horizont. Mit ihm konnte man die Höhe der Sonne oder des Nordsterns einigermaßen abschätzen, indem man einen Schieber ein Messlineal entlang schob, bis der Schieber ein genaues Maß zwischen Horizont und Sonne bildete. Bei der Sonne konnte man sich schon die Augen schädigen und deshalb wurde der Jakobsstab auch umgekehrt mit einem schwarzen Spiegel benutzt. Abgelöst wurde der Jakobsstab durch Oktanten und Sextanten.
Zur Bestimmung der Breite gibt es insbesondere zwei Möglichkeiten, die Nordsternbreite und die Mittagsbreite. Der Nordstern ist nur auf der Nordhalbkugel zu beobachten. Er ist nicht nur dazu geeignet, die Nordrichtung anzugeben. Eine Besonderheit besteht auch darin, dass seine Höhe über dem Horizont auch die Breite ist, auf der gesegelt wird. Eine Höhenmessung ist allerdings nur in der Dämmerung möglich, solange der Horizont noch sichtbar ist.
Der Nordstern steht allerdings nicht ganz exakt im Norden, sondern beschreibt im Laufe von 24 Stunden einen kleinen Kreis mit einem Durchmesser von weniger als 1°. Nehmen wir an, dass sein Licht senkrecht auf den Nordpol fällt und sein Bildpunkt damit der Nordpol wäre. Dann ist der Einfallswinkel seines Lichtes und somit seine Höhe über dem Horizont identisch mit der Breite, auf der man sich gerade befindet. Bei einem Standort direkt auf dem Nordpol würde seine Höhe mit 90° festgestellt werden, denn er stände dort im Zenit. Bei einem Standort am Äquator würde er, wenn überhaupt, bei 0° gesehen werden. Vernachlässigt man seinen kleinen Kreisdurchmesser von knapp 1°, dann führt das zu einer Abweichung in der Breite von ebenfalls knapp 1°, also 60 nm in Nord-Süd Richtung.

Die Mittagsbreite zu bestimmen ist ein Ritual, das seit Jahrhunderten auf Seeschiffen abläuft. Der Navigator tritt am Mittag mit dem Sextanten, früher auch mit dem Jakobsstab oder Oktanten an Deck, um die Höhe der Sonne während ihrer Kulmination festzustellen. In dem Moment steht die Sonne über demselben Meridian wie das eigene Schiff und wird exakt im Süden (oder Norden) gesehen.
Man sollte ungefähr wissen, wann Schiffsmittag ist, um nicht so lange mit dem Sextanten auf der Lauer liegen zu müssen. Einige Minuten davor oder danach verändert sich die Höhe der Sonne nicht messbar. Man hat also Zeit, die Kulmination der Sonne beobachten zu können, kann bis zu drei Minuten Pause von Messung zu Messung verstreichen lassen.
Sobald die Kulminationshöhe feststeht, kann der Breitengrad mit Hilfe einer kleinen Rechnung bestimmt werden. Vorher muss man die abgelesene Höhe noch beschicken, um den Einfluß von Durchmesser der Sonnenscheibe, Refraktion und Standhöhe auszugleichen. Ein gutes Mittelmaß sind 13’, die zu einer Sextantenablesung addiert werden müssen, wenn der Unterrand der Sonne beobachtet wurde. Für die nachfolgende kleine Rechnung braucht man die Deklinationsbreite δ der Sonne. Diese konnte man einer Tabelle entnehmen. Später wurde die Deklination genauer in nautischen Jahrbüchern erfasst. Viel zu rechnen gibt es dabei nicht. Es gilt
bei Kulmination der Sonne im Süden: 90° – Höhe + Deklination,
bei Kulmination der Sonne im Norden: Höhe – 90° + Deklination .
Auch auf der Nordhalbkugel kann die Sonne im Norden kulminieren, wenn der Standort zwischen dem Äquator und der Deklinationsbreite liegt. Zu beachten ist, dass südliche Deklinationen mit einem negativen Vorzeichen gekennzeichnet sind. Nördliche Deklinationen und die Höhe bekommen ein positives Vorzeichen. Ein negatives Ergebnis weist also auf eine südliche Breite hin. Hierzu drei Beispiele:
- Beispiel 1: Deklination δ = 21° N, h = 65°, Kulmination im Süden
Ergebnis: φ = 90° – 65° + 21° = 46° = 46° N
- Beispiel 2: Deklination δ = 14° S, h = 53°, Kulmination im Norden
Ergebnis: φ = 53° – 90° -14° = -51° = 51° S
- Beispiel 3: Deklination δ = 23° N, h = 84°, Kulmination im Norden
Ergebnis: φ = 84° – 90° + 23° = 17° = 17° N
Für die Berechnung der Grundfunktionen Mittagsbreite und auch der Folgenden, Mittagslänge und Chronometerlänge, wurde ein kleines EXCEL Sheet zum Herunterladen erstellt.
Dieses EXCEL-Programm ist auch auf allen Mobilgeräten lauffähig, auf denen die EXCEL App installiert ist, also auch auf Smartphones. Es besitzt Datenbanken mit den Positionen des Bildpunktes der Sonne und zur Sextantenbeschickung. Die Sonnenpositionen müssen jährlich nachgeladen werden. Dafür steht eine Downloaddatei mit den vorausberechneten Sonnenpositionen bis zum Jahre 2025 zur Verfügung.
nautical-sun-almanac-2019-2025 rev
Wie das Nachladen genau funktioniert wird in diesem Beitrag gezeigt.
Das folgende Bild zeigt einen Ausschnitt aus der Eingabenmaske des EXCEL-Sheets, der zur Bestimmung der Mittagsbreite vorgesehen ist. Datum und Uhrzeit werden links oben eingegeben, wobei eine minutengenaue Zeit sogar ausreicht. Dafür zieht das Programm die Deklination aus seiner Datenbank, die am 16. Apr 2020 um 12:45 genau 10,40° N beträgt. Sie wird auf der rechten Seite oben auch angezeigt.

Nach Eingabe der Sextantenablesung, hier 66° 14,7′ und des Indexfehlers, hier -6′ wird rechts im Infoblock die beobachtete Höhe, also die berichtigte Höhe mit 66°21,28′ ausgegeben. Der Indexfehler ist bei Plastiksextanten recht hoch, vor allem dann, wenn sie in der Sonne gelegen und sich daduch erwärmt haben. Er sollte dann immer neu bestimmt und neu eingegeben werden. Nomalerweise beträgt der Unterschied zwischen Sextantenablesung und beobachteter Höhe bei aufgesetzter Sonne etwa 13′. Dazu muss dann noch die Indexberichtigung addiert werden.
Die im Ergebnisblock rechts unten angezeigte Mittagsbreite ist natürlich davon abhängig, ob die Sonne im Süden oder Norden beobachtet wird. Hier ist also die entsprechende Himmelsrichtung einzugeben.
Das EXCEL Sheet vereinfacht die Bestimmung der Mittagsbreite dadurch, dass man kein nautisches Jahrbuch mitschleppen muss und die Sextantenbeschickung nach Eingabe der Sextantenablesung im Hintergrund abläuft.
2. Die Mittagslänge
Der Wunsch nach einer einfachen Methode zur Bestimmung der Länge, nur unter Anwendung der Grundrechenarten, führte insbesondere in der Szene der Blauwassersegler zur Bestimmung der sogenannten Mittagslänge. Das Verfahren hat keine historischen Wurzeln, was nicht verwunderlich ist, weil man zu seiner Benutzung genau gehende Uhren und ein Nautisches Jahrbuch gebraucht hätte. Der Hauptnachteil besteht in dem recht umständlichen Messvorgang mit dem Sextanten. Außerdem ist diese Länge nur einmal am Tag für den Moment des Schiffsmittags bestimmbar. Messfehler steigen mit größer werdender Entfernung zur Deklinationsbreite, weil die Sonne dann sowieso immer tiefer steht.
Trotzdem soll dieses Verfahren vorgestellt werden, denn es hat eine Zeitlang unter Seglern eine Rolle gespielt. Das Argument einer einfachen Berechnung spielt inzwischen keine Rolle mehr. Die Methode hat deshalb auch keine praktische Bedeutung für die Zukunft.
Am Schiffsmittag, bei der Bestimmung der Mittagsbreite, befindet sich die Sonne auf demselben Längengrad wie das Schiff und so stellte man sich die Frage, ob man nicht herausbekommen könnte, welcher Längengrad das ist. Da die Sonne in einer Stunde 15° zurücklegt, müsste man um 13:00:00 UTC doch auf 15° westlicher Länge sein. So einfach ist das jedoch nicht. Erstens überquert die Sonne den Greenwicher Nullmeridian nicht um 12:00 UTC, sondern infolge der Zeitgleichung etwas davor oder danach. Die Zeit 12:00:00 UTC ist genaugenommen nur ein Jahresmittelwert. Zweitens haben wir bei der Bestimmung der Mittagsbreite gesehen, dass die Sonne minutenlang auf scheinbar derselben Höhe verharrt. In dieser Zeit überquert sie dann zweieinhalb Längengrade, ohne dass wir dieses mit unserem Sextanten bemerken könnten und legt dabei 150 nautische Meilen zurück. Wann genau in dieser Zeitspanne ist also der Schiffsmittag?
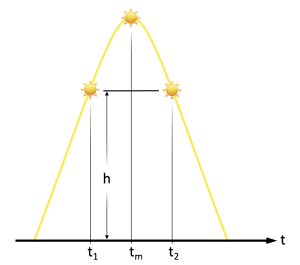
Das erste Problem lässt sich lösen, indem man anstelle einer kleinen Tabelle mit der Zeitgleichung ein nautisches Jahrbuch mitschleppt. Aus diesem kann für die genaue Zeit des Schiffsmittags der Greenwicher Stundenwinkel Grt direkt herausgelesen und auf die geografische Länge umgerechnet werden. In jedem Fall braucht man aber die sekundengenaue Zeit des Schiffsmittags.
Das macht eine Menge Arbeit, übt aber im Umgang mit einem Sextanten. Mindestens eine halbe Stunde vor dem erwarteten Schiffsmittag, besser etwas mehr, wird die Sonnenhöhe h gemessen. Sextantenablesung und sekundengenaue Uhrzeit t1 werden notiert. Etwa dieselbe Zeit nach dem Schiffsmittag versucht man durch mehrere Messungen die Zeit t2 herauszubekommen, in der die Sonne die gleiche Höhe h wie bei der Vormittagsmessung hatte. Das ist ganz klar eine knifflige Sache, die durch Seegang usw. ziemlich erschwert sein kann. Der Mittelwert der festgestellten Zeiten ist dann der genaue Schiffsmittag tm. Zum zweiten Zeitpunkt kann die Sonne jedoch auch hinter Wolken versteckt sein. Einige auf Vorrat gemessene Vormittagshöhen könnten hier ganz hilfreich sein.
Zur Berechnung des Zeitmittelwertes werden die beiden festgestellten Zeiten addiert und die erhaltene Summe durch zwei geteilt:
![]()
Aufpassen muss man bei einem Datumsübergang. Ein Mittelwert zwischen 23:00:00 UTC und 2:00:00 UTC beträgt 00:30:00 UTC und nicht 12:30:00 UTC. Für diese Zeit und das Tagesdatum wird jetzt aus dem Nautischen Jahrbuch der Stundenwinkel Grt herausgelesen. Dabei muss beachtet werden:
- Schiff auf Ostlänge: λ = 360° – Grt
- Schiff auf Westlänge: λ = Grt
Das Excel-Sheet kann dabei helfen. Beispielsweise wurde am selben Tag schon um 11:56:04 UTC die Höhe der Sonne gemessen. Am Sextanten wurden 63° 4,4‘ abgelesen. Dieser Wert wird in der EXCEL-Eingabemaske eingetippt, damit er nicht vergessen wird. Doch jetzt kommt erst mal der Schiffsmittag, an dem wir die Sonne nochmals schießen müssen, um die Breite zu bestimmen. Das ist weiter oben schon geschehen und es wurde eine Mittagsbreite von 34° 2,59′ N festgestellt. Jetzt stellen wir am Sextanten wieder den Wert 63° 4,4′ ein und legen uns auf die Lauer. Genau um 13:46:28 UTC berührt die sinkende Sonne im Teleskop wieder die Kimm.
Mit Papier und Bleistift könnten wir jetzt rechnen: Seit der ersten Messung sind 1 Stunde, 50 Minuten und 24 Sekunden vergangen. Schiffsmittag war zur Hälfte dieser Zeit, also genau um 12:51:16 UT.

Wir haben aber das EXCEL-Sheet, das uns die Rechnerei mit den Stunden und Minuten abnimmt. Wir erhalten so die sekundengenaue Zeit des Schiffsmittags ganz schnell. Das Programm rechnet auch den Transitus des betreffenden Tages aus. Die Zeitabweichung des Transitus von 12:00:00 UTC ist der Wert der Zeitgleichung und die beträgt an dem verwendeten Datum nur 18 Sekunden. Im Nautischen Jahrbuch könnte man jetzt für den Schiffsmittag den Greenwicher Stundenwinkel heraussuchen. Das macht auch die EXCEL Datei und findet dafür in der Datenbank eine Mittagslänge von 12,895° und das sind 12° 53,68′.
Das Ergebnis ist die Länge am Schiffsmittag. Den aktuellen Schiffsort, später um 13:46:28 UTC, erhält man durch Koppeln unter Berücksichtigung von Kurs und gefahrener Geschwindigkeit während der letzten Stunde.
Mit dieser Methode kann der Längengrad mehr oder weniger genau genau bestimmt werden, ist aber verbunden mit einer Menge anstrengender Arbeit mit dem Sextanten. Man sollte aufpassen und sich nicht zu sehr der Sonne aussetzen. Ganz wichtig dabei ist, den Zeitpunkt t2 nicht zu verpassen. Das Rechnen beschränkt sich nur auf Grundrechenarten, weshalb die Methode auch mal ihre Zeit hatte. Mit einem Elektronenrechner kann man mathematikintensivere und bessere Methoden benutzen, mit denen die Länge auch zu anderen Zeiten bestimmt werden kann als nur für den Schiffsmittag.
Wird ein Plastiksextant verwendet, dann sollte sich dieser für die Vormittagsmessung und die Nachmittagsmessung auf gleichem Temperaturniveau befinden, also nicht in der Sonne liegen lassen. Eine Korrektur unterschiedlicher Indexfehler ist bei dieser Methode nicht möglich.
3. Die Chronometerlänge
Die geografische Breite war also relativ einfach und mit hoher Genauigkeit bestimmbar. Eine aktuelle Breite konnte durch Koppeln gefunden werden. Die Bestimmung des Längengrades galt über einen Zeitraum von 400 Jahren als unmöglich.
So war es üblich, dass die Schiffe in bekannten Gewässern an einer Küste entlang wochenlang Breiten absegelten, bis die gewünschte Breite erreicht war. Erst dann konnten sie den Breitenkreis entlang eine Überfahrt zu einem bekannten Hafen antreten. Zahlreiche Schiffe gingen verloren, weil sie sich in der Länge verschätzten und früher als gedacht an Land gerieten. Monatelange Fahrten ohne frische Lebensmittel und Wasser rafften die Mannschaften durch Skorbut dahin. Das sogenannte Längenproblem wurde zunehmend zu einem wirtschaftlichen Problem.
Bereits 1600 setzte der spanische König ein Preisgeld aus, um das Längenproblem lösen zu können, doch er blieb damit erfolglos. Mehr als hundert Jahre später, im Jahre 1714 folgte das englische Parlament diesem Beispiel und setzte bis zu 20 000 Pfund Preisgeld für eine praktikable Lösung des Längenproblems aus. Anlass war der Untergang von vier Schiffen 7 Jahre vorher, die auf den Klippen der Skilly-Inseln zerbrachen und dem etwa 1500 Seeleute zum Opfer fielen. Das Preisgeld war aufgestaffelt nach Genauigkeit: 10 000 Pfund für 1° Präzision, 15 000 Pfund für 40′ Präzision 20 000 Pfund für 30′ Präzision.
Erst zehn Jahre später beschäftigte sich John Harrison damit. Er war eigentlich Tischler, hatte aber bereits eine Uhr mit Holzzahnrädern gebaut und ihn ließ die Vision nicht mehr los, eine genau gehendes Schiffsuhr zu bauen. Damals gab es zwar schon Verfahren, wie die Länge aus der Bedeckung der Jupitermonde oder des Abstands unseres Erdmondes hergeleitet werden konnte, aber diese Verfahren waren an Bord der üblichen Schiffe nicht praktikabel, denn sie waren viel zu selten. Man brauchte praktikablere Methoden.

Mit einem ersten Uhrenexemplar von Harrison gelang eine Testfahrt, bei welcher die Genauigkeit der Methode bestätigt werden konnte. Das Preisgeld wurde jedoch nicht gezahlt, weil die Testreise nicht ganz den Anforderungen entsprach. Es konnte auch alles Zufall gewesen sein, meinten einige Kritiker. Außerdem gab es Widerstände und Bedenken. Die Zuverlässigkeit eines technischen Instrumentes wurde angezweifelt. Insbesondere vom Hofastronom des englischen Königshauses, Nevil Maskelyne, der auf die Monddistanz Methode setzte, weil die unabhängig von technischen Instrumenten ist. Hier könnte man an die jüngere Geschichte erinnert sein. Sogar der Taschenrechner hatte es einst schwer, in der Astronavigation die Logarithmen zu verdrängen.
Erst als James Cook 1775 von seiner zweiten Weltreise zurückkehrte und die gute Qualität eines heute mit H4 bezeichneten Modells eines Harrison Chronometres bestätigte, galt auch in Astronomenkreisen das Längenproblem als gelöst. Harrison wurde ein Preigeld von 10 000 £ zugesprochen. Eine Weiterentwicklung, heute mit H5 bezeichnet, wurde von König Georg III persönlich getestet. Dafür erhielt Harrison weitere 8 750 £.
Nach der H5, die damals etwa 500 £ kostete, bauten Uhrmacher die Modelle nach und die Preise sanken. Die ersten in Serie produzierten Marine Chronometer waren schon 1790 verfügbar. Welche Bedeutung sie hatten zeigt die Tatsache, dass die Beagle auf ihrer Forschungsreise gleich 22 Stück davon an Bord hatte. Mitte des 19 Jahrhunderts war jedes seegehende Schiff mit mindestens zwei Chronometern ausgestattet und der Kapitän besaß noch sein eigenes.

Doch wie wird die Länge mit Hilfe eines Chronometers überhaupt bestimmt? Die Sonne legt in einer Stunde 15° zurück. Das ist sozusagen ihre Winkelgeschwindigkeit. Wenn man an Bord auf einem Chronometer 14:00:00 GMT (Greenwich Mean Time) ablesen würde und die Bordzeit wäre 16:00:00 Uhr, dann wäre die Sonne noch 2 Stunden östlich vom eigenen Standort. In Grad umgerechnet ist die Sonne also schon 2h ≙ 30° westlich von Greenwich und erreicht den Meridian des Schiffsortes, wenn sie weitere 30° zurückgelegt hat. Die Standortlänge ist also 60° W. Die Zeitgleichung wäre allerdings auch noch zu berücksichtigen, denn die Sonne passiert den Greenwicher Nullmeridian nicht genau um 12:00:00 GMT, sondern bis zu einer Viertelstunde früher oder später. Man müsste also nur die Differenz zwischen Chronometerzeit und berichtigter Bordzeit mit der Winkelgeschwindigkeit der Sonne multiplizieren und hat den Längengrad.
Das ist formal richtig, hat aber einen Haken und der besteht darin, dass die Bordzeit bzw. Ortszeit nicht bekannt ist. Eine Ortszeituhr gibt es leider auch nicht. Wie der Name schon sagt, ändert sich die Ortszeit nicht nur mit dem Gang der Sekunden, sondern auch mit der Ortsveränderung eines segelnden Schiffes.
Auf den Fahrten zum Test der Harrison Chronometer waren deshalb auch immer Astronomen an Bord, die die Ortszeit feststellen mussten. Diese wurde durch Messung der Höhe eines Gestirns, beispielweise der Sonne, an Hand des nautischen Dreiecks errechnet. Die Summe aus Ortszeit und Zeitgleichung war dann die mittlere Ortszeit, und erst damit wurde der Zeitunterschied zur Chronometerzeit ausgerechnet. Dieser Zeitunterschied, mit 15°/ Stunde multipliziert ergab dann erst die Standortlänge, die sich auf den Nullmeridian bezog.
Die Lage des Nullmeridians ist willkürlich. In der Antike lief er durch die Kanaren, weil das die am weitesten westlich liegenden bekannten Landteile waren. Die Franzosen ließen ihn durch Paris laufen und die Engländer durch den Londoner Stadtteil Greenwich. Auf der internationalen Meridiankonferenz 1884 in Washington, D. C. wurde der Verlauf durch Greenwich festgelegt. Anteil daran hatten die vielen von Nevil Maskelyne herausgegebenen Almanache und Monddistanz Tabellen, die sich alle auf Greenwich bezogen und nach denen die Mehrzahl der Schiffe aller Nationen bereits navigierten. Nur die Franzosen behielten ihren Nullmeridian durch Paris noch einige Jahre.
Eine Schwierigkeit bestand darin, dass die Chronometer nach langen Fahrten immer mal justiert werden mussten. Befand man sich an einem Ort, dessen Position bekannt war, dann konnte man dessen Ortszeit durch eine Höhenmessung bestimmen und diese Zeit unter Verwendung der Ortslänge auf GMT zurückrechnen. Möglich war auch eine Zeitbestimmung durch Messung einer Monddistanz. In verschiedenen Häfen gab es auch Zeitbälle. Der Ball wurde Zeit an einem Mast hochgezogen und zu einer bestimmten Zeit wieder fallen gelassen. Im Royal Observatorium Greenwich geschah das um 1:00:00 GMT. Die Bälle waren so positioniert, dass sie weithin sichtbar waren, auch für die Schiffe, die noch am Anker lagen. Das erleichterte das Stellen der Uhren Mit dem Aufkommen des Seefunks gab es dann Zeitzeichen und die Bälle wurden fast überall wieder abgebaut.
3.1 Berechnung am Nautischen Dreieck
Die Methode der Chronometerlänge verbreitete sich rasch, hatte allerdings auch ihre Schwachstellen. Die Genauigkeit hing ja nicht nur von der Ganggenauigkeit des Chronometers ab, sondern auch von der Standortbreite. Diese wurde nämlich zu einem ganz anderen Zeitpunkt bestimmt, z. B. am Vortag und in der Zwischenzeit konnte eine erhebliche Ortsveränderung eingetreten sein. Dieses Vorgehen, die getrennte Bestimmung der Ortskoordinaten Länge und Breite, war jedoch charakteristisch für die damalige Zeit und wurde erst ab Mitte des 19. Jhd. von der modernen Astronavigation abgelöst.
Bild 6 zeigt das nautische Dreieck in zwei unterschiedlichen Konstellationen. Die Ecken der Dreiecke werden gebildet von Z dem Standort des Schiffes, X dem Bildpunkt der Sonne oder eines anderen Gestirns und N dem Pol, im Beispiel der Nordpol. Die Dreieckseiten sind s, p und b. Diese Seiten sind die Komplemente von Gestirnshöhe, Deklination und Standortbreite. Unter Komplement wird die Differenz eines Winkels zu 90° verstanden. Komplemente erleichtern das Schreiben der Gleichungen ganz erheblich. In der folgenden Tabelle sind die Dreieckseiten und ihre zugehörigen Komplemente definiert: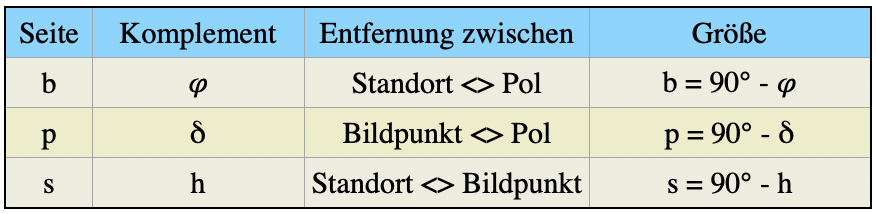
Bild 6 zeigt, dass sich die Länge aus dem Greenwicher Stundenwinkel Grt und dem Polwinkel ![]() leicht berechnen lässt. Auf der linken Seite des Bildes ist es einfach die Summe von Grt +
leicht berechnen lässt. Auf der linken Seite des Bildes ist es einfach die Summe von Grt + ![]() , weil die Sonne vom Standort aus östlich gesehen wird und auf der rechten Seite ist es die Differenz Grt –
, weil die Sonne vom Standort aus östlich gesehen wird und auf der rechten Seite ist es die Differenz Grt – ![]() , weil die Sonne im Westen der Beobachterposition steht. Man muss also nur den Polwinkel tau berechnen.
, weil die Sonne im Westen der Beobachterposition steht. Man muss also nur den Polwinkel tau berechnen.

Der Kosinus Seitensatz, die Geheimwaffe der Astronavigation, lautet für diesen Fall:
![]()
Nach Umstellung auf die Winkelfunktion ![]() und Benutzung der Komplemente in aufeinanderfolgenden Schritten folgt daraus:
und Benutzung der Komplemente in aufeinanderfolgenden Schritten folgt daraus:
![]()
Schließlich wenden wir noch die Umkehrfunktion an, um aus der Winkelfunktion den Winkelwert zu erhalten:
(1) ![]()
Zur Chronometerlänge ist es jetzt nur noch ein kleiner Schritt:
(2) ![]()
Das Stenchen besagt nur, dass die berechnete Länge nicht in das Gradsystem der Erde mit 180 Ostgraden und 180 Westgraden passt und deshalb eine Umrechnung erforderlich ist. Ob Grt und ![]() addiert oder
addiert oder ![]() von Grt subtrahiert werden muss, hängt davon ab, ob die Sonne östlich oder westlich beobachtet wird. Wenn die Höhe der Sonne am Vormittag gemessen wurde, dann muss addiert werden.
von Grt subtrahiert werden muss, hängt davon ab, ob die Sonne östlich oder westlich beobachtet wird. Wenn die Höhe der Sonne am Vormittag gemessen wurde, dann muss addiert werden.
3.1 Berechnung durch das EXCEL Sheet
Die Chronometerlänge kann auch ganz einfach mit Hilfe der EXCEL Datei berechnet werden. Bild 7 zeigt dafür die Eingabefelder auf der linken Seite. Neben Datum, und Uhrzeit der Sextantenmessung und der Sextantenablesung selbst sind die gegeisste Standortbreite (Koppelbreite) und die Peilung der Sonne einzugeben. Auch für die Indexberichtigung gibt es hier nochmal ein Feld. Der imBeispiel eingetragene Wert entspricht einem Indexfehle von +6′ und entstammt einem Plastiksextanten. Zur Berichtigung muss dann ein Wert von -6′ eingegeben werden. Auf der rechten Seite werden als Information der Grt, die Deklination und die berichtigte Höhe ausgegeben.
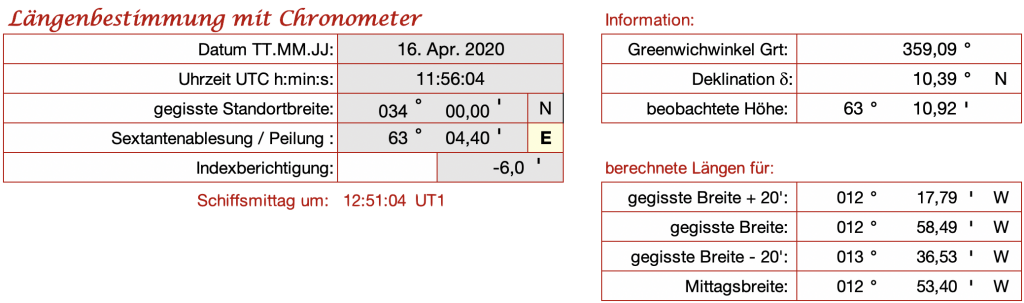
Wird diese Standlinie an einem Tag zweimal ermittelt, einmal vormittags und einmal nachmittags, oder mit zwei verschiedenen Himmelskörpern zum gleichen Zeitpunkt, so erhält man zwei sich kreuzende Linien und der Standort ist der Kreuzungspunkt der Linien. Im Rahmen dieses Programmms kann allerdings nur eine Linie ausgegeben werden.
Wird in der Zeit zwischen den Messungen gesegelt, dann muss die erste Standlinie parallel verschoben werden und zwar in Kursrichtung um die gefahrene Strecke. Diese Navigationsmethode war in der zweiten Hälfte des 19. Jahrhunderts eine Standardmethode zur Positionsbestimmung auf See und sogar verbindlich für die Amerikanische Marine.
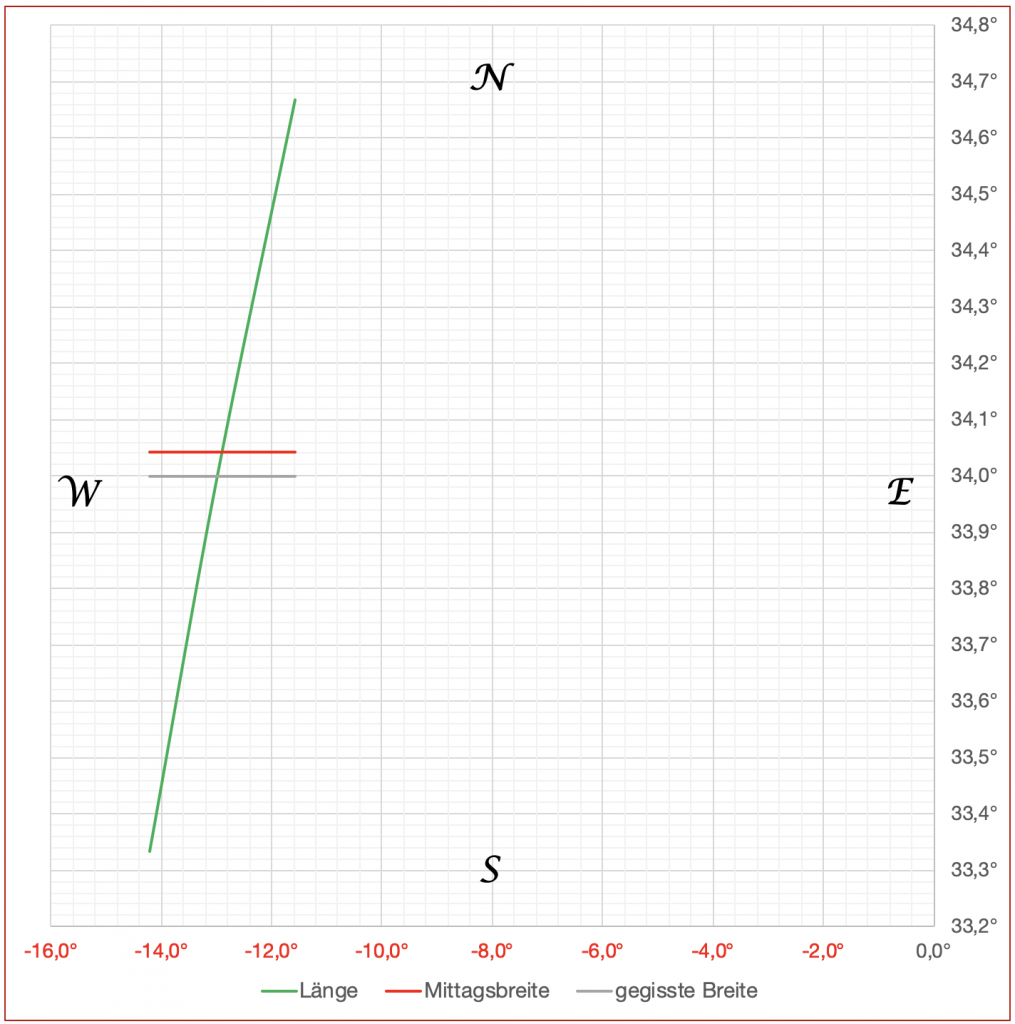
Wenn mit dem Programm basic sun navigator die Mittagsbreite ermittelt wurde und z. B. schon vormittags die Chronometerlänge festgestellt wurde, dann berechnet das Programm dafür auch die Mittagslänge und somit einen Standort. Das Ergebnis ist in der nebenstehenden Grafik zu sehen. Die rot dargestellte Linie ist die Mittagsbreite und die grüne Linie eine Sumnerlinie.
Bei genauem Hinsehen ist zu erkennen, dass diese Sumnerlinie in Abweichung von der traditionellen Art etwas gekrümmt ist. EXCEL berechnet nämlich für die Grafik insgesamt fünf Stützpunkte. Die Sonne wurde im Südosten gepeilt und so ist auch erkennbar, dass die grüne Sumnerlinie ein Stück des Kreises um den Bildpunkt der Sonne ist. Für die Berechnung des Schnittpunktes wurden allerdings Geraden benutzt.
4 Klassische Berechnung der Chronometerlänge
Als es noch keine elektronischen Rechenmaschinen gab, musste das Navigieren ja auch irgendwie funktionieren. Damals gab es Logarithmentafeln, aber wie ging man damit um? Was Logarithmen sind, haben viele inzwischen schon vergessen. Wir wissen vielleicht noch, dass damit Multiplikationen und Divisionen auf Additionen und Subtraktionen zurückgeführt werden können. Logarithmen sind bekanntlich die Exponenten einer Basiszahl. Als Basis wird meist die Zahl 10 benutzt. So ist der Logarithmus von 100 die Zahl 2, weil die Basis2 = 100 ist. Der Logarithmus von 1.000 ist dann 3, denn Basis3 ist 1.000 und wenn diese Logarithmen addiert werden, dann kommt 2 + 3 = 5 heraus und das ist eine 1 mit fünf nullen, also 100 mal 1000. Logarithmen sind in der Regel gebrochene Zahlen. So ist der Logarithmus von 27,47894 die Zahl 1,439, weil 101,429 = 27,47894 ist. Mit Logarithmen rechnet man in einem sogenannten Bildbereich und das ist einfacher. Am Ende muss das Ergebnis in den Originalbereich zurück transformiert werden. Zum hin- und her Transformieren stand diverses Tafelmaterial zur Verfügung. So wurden auch Logarithmen von Winkelfunktionen tabelliert, z. B. lg sin 45,8° = -0,14454.
Um ohne Unterbrechung optimal mit Logarithmen rechnen zu können, sollte in den Gleichungen nur multipliziert oder dividiert werden. Damit bleibt man im Bildbereich, wo man nur addieren und subtrahieren muss. Der Kosinus Seitensatz muss deshalb so verändert werden, dass in der Hauptgleichung nur noch multipliziert oder dividiert werden muss. In der Gleichung zur Bestimmung der Chronometerlänge
(3) ![]()
subtrahieren wir auf beiden Seiten eine 1:
![]()
Damit erhalten wir: (4) ![]()
Ein Additionstheorem der trigonometrischen Funktionen lautet:
![]()
Damit vereinfachen wir den Klammerausdruck im Zähler der Gl.4 und erhalten:
(5) ![]()
Der Zähler dieser Gleichung kann jetzt mit einer sogenannten Verwandlungsformel aus dem Formelbuch umgestellt werde. Diese Verwandlungsformel lautet:
![]()
Nach ihrer Anwendung erhalten wir schließlich den völlig umgeformten Kosinus Seitensatz, der für die Berechnung mit Logarithmen optimal ist. Er lautet:
(6) ![]()
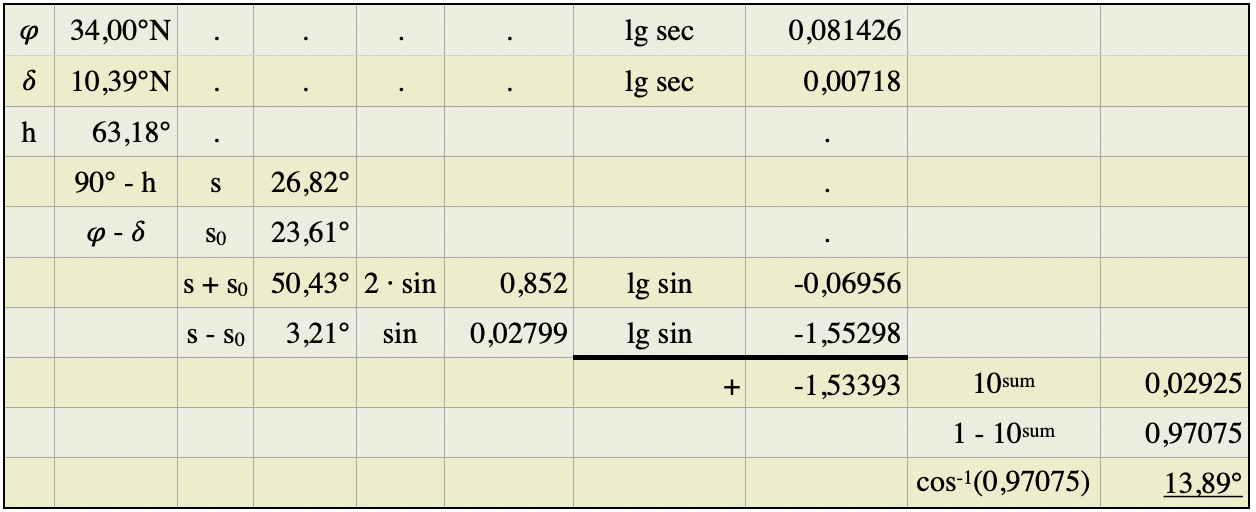
In dieser Gleichung sind s = 90° – h der Zenitabstand und ![]() die sog. Meridiandistanz. letzteres ist die algebraische Differenz zwischen Breite und Deklination, so wie sie am Schiffsmittag herrscht. Besitzen sie ein gleichnamiges Vorzeichen, dann sind sie zu subtrahieren. Bei ungleichnamigem Vorzeichen sind sie zu addieren. Zum Schluss soll dafür noch ein Beispiel berechnet werden. Dafür werden die Zahlen aus dem obigen Beispiel verwendet.
die sog. Meridiandistanz. letzteres ist die algebraische Differenz zwischen Breite und Deklination, so wie sie am Schiffsmittag herrscht. Besitzen sie ein gleichnamiges Vorzeichen, dann sind sie zu subtrahieren. Bei ungleichnamigem Vorzeichen sind sie zu addieren. Zum Schluss soll dafür noch ein Beispiel berechnet werden. Dafür werden die Zahlen aus dem obigen Beispiel verwendet.
In dieser Tabelle sind die logarithmierten Sekanten jeweils die Logarithmen des Kehrwertes der Kosinusfunktionen der Winkel, also lg(1/cos ![]() und lg(1/cos ∂). Dadurch können alle Logarithmen addiert werden.
und lg(1/cos ∂). Dadurch können alle Logarithmen addiert werden.
Der Polwinkel von 13,89° bzw. 13° 53,47′ ist der Winkel, bzw. die Länge, den der Bildpunkt der Sonne noch bis zum Schiffsmittag zurücklegen muss. Ein Greenwicher Stundenwinkel Grt stand in damaligen Tabellen nicht zur Verfügung, nur eine Tabelle mit der Zeitgleichung und die hatte am 16. April 2020 nur einen Wert von 18,4 Sekunden.
Wie auf klassische Art aus dem Polwinkel die Länge berechnet wurde, zeigt die nachstehende Tabelle, die einem alten Lehrbuch entlehnt worden ist. Indem wir zunächt den Polwinkel von 13,89° aus obiger Tabelle durch 15°/h teilen, erhalten wir die Zeit bis zum Schiffsmittag und die beträgt hier 0,926075 h bzw. 00:55:34 h. Den Rest zeigen die weiteren Tabellenzeilen b bis g.
Die berechnete zeitlichen Entfernung des Standortes vom Londoner Stadtteil Greenwich von 00:51:56 h kann jetzt durch Multiplikation mit 15°/h die Entfernung in Grad umgerechnet werden und liefert die Länge des Standortes mit 12° 59,00′ W.
Neben der hier vorgestellten Methode gibt es noch eine ältere und sogar noch etwas einfachere Methode zur logarithmischen Berechnung der Chronometerlänge. Sie beruht auf der logarithmischen Berechnung der Länge bereits mit der Gl. 5. Diese Methode hat Kapitän Sumner im Zusammenhang mit seiner Methode in seinem Buch vorgestellt. Sie wird in dem Beitrag dazu erläutert.
Unter Verwendung des Grt bzw. GHA, wie das dann später üblich wurde war die Rechnung sehr viel einfacher. Den Grt lieferte ein nautischer Almanach. In diesem Beispiel müssen wir ihn aber selbst berechnen. Er ergibt sich als Stundenwinkel von Chronometerzeit, Zeitgleichung und 12h, was dann 23:56:22h sind und mit 15°/h einen Grt von 359,0917° ergeben. Da die Beobachtung noch vor dem Mittag erfolgte, ergibt sich die Standortlänge dann als Summe von Grt und Polwinkel mit 359,0917° + 13,892° = 372,8937°. Da hier wegen des Überlaufs 360° abgezogen werden müssen, ist es eine Westlänge und die beträgt dann genau 12,9837° W oder 12° 59,02′ W.
Links:
nach oben ♦ Die Sonne am Himmel ♦ Gauß und das Zweihöhenproblem ♦ Thomas H. Sumner, Begründer der Standliniennavigation ♦ Die Methode des Marcq Saint Hilaire ♦ Navigieren mit Excel ♦ Ein wenig Sextantenkunde ♦ Sextantentest Mark 25 ♦ Downloads ♦ Home