Dead Reckoning - SY-Zephir

Darunter wird eine einfache und seit Jahrhunderten benutzte Navigationsmethode verstanden. Im englischen wird sie als Dead Reckoning bezeichnet, was soviel wie totale Berechnung bedeutet. Zur Durchführung verwendet der Navigator einfache, aber zuverlässige Werkzeuge, um drei Dinge zu verfolgen:

Kompassrichtung des Bootes
Geschwindigkeit durchs Wasser
Zeit, die für jede Kursrichtung und jede Fahrtgeschwindigkeit aufgewendet wurde

Mit diesen Informationen konnte der Navigator Route und Entfernung berechnen, die das Schiff zurücklegt und in einer Seekarte markieren. Mit einer sorgfältig durchgeführten Koppelnavigation sind Fehlerraten bis herunter zu 5% erreichbar. Das Koppeln wurde früher angewendet, wenn sich das Schiff nachts in komplizierten Gewässern bewegen musste. Das betraf jedoch meist nur Kriegsschiffe. Handelsschiffe gingen in so einem Fall meist vor Anker. Doch wozu brauchen wir heute noch eine Koppelnavigation?

Wozu noch Koppelnavigation

Die astronomische Navigation erfordert zu einer Standortbestimmung mindestens zwei Gestirnshöhen, entweder von zwei unterschiedlichen Gestirnen oder von einem Gestirn wie der Sonne zu unterschiedlichen Zeiten. Dabei sollten sich die Höhengleichen bzw. Azimute, der beobachteten Gestirne in einem möglicht rechten Winkel schneiden. Bei Anwendung des Höhenverfahrens nach Hilaire sollte der Schnittwinkel nicht kleiner als 30° sein, damit der Schnittpunkt der Standlinien noch genau genug herausgelesen werden kann. Werden analytische Methoden verwendet, dann kann der Winkel spitzer ausfallen, sollte 20° aber auch nicht unterschreiten. Um das zu erreichen, muss zwischen den Beobachtungen eine ausreichend lange Zeit vergehen. Wenn nicht gerade Totenflaute herrscht, wird man sich vom Ort der ersten Beobachtung entfernen. Doch mit jeder Entfernungsänderung vom Bildpunkt ändert sich auch die Höhe, in der ein Gestirn beobacht wird und das auch dann, wenn es gedanklich in seiner Position am Himmel eingefroren wird.
Es geht jetzt also darum, aus den unterschiedlichen Kursen und Strecken, zwischen den Beobachtungen einen resultierenden Kurs (CMG = course made good), eine resultierende Gesamtstrecke über Grund (DMG = distance made good) und eine resultierende Geschwindigkeit (VMG = velocity made good) zu finden. Dabei muss zusätzlich eine eventuell vorhandene Strömung, aber auch ein Versatz durch Wind berücksichtigt werden. Man segelt eigentlich immer Kurse, bei denen der Wind optimal ausgenutzt wird. Beim Segeln, z. B. mit halbem Wind, fällt der scheinbare Wind genau von der Seite ein. Dieser Zustand ermöglicht die höchste Geschwindigkeit. Das Boot fährt dabei aber nicht in Kielrichtung. Vielmehr ist der Bug etwas in den Wind gedreht, wodurch das anströmende Fahrwasser seitlich gegen den leicht quer stehenden Kiel und den Unterwasserrumpf drückt. Zwischen diesem dynamischen Wasserdruck und dem Winddruck von der anderen Seite auf das Segel stellt sich ein Gleichgewicht ein. Der in Kielrichtung weisende Kompass zeigt dann jedoch nicht mehr den Fahrkurs an. Der Wind trifft außerdem die Freibordfläche des Rumpfes und die Aufbauten, die nicht unbedingt zum Kräftegleichgewicht beitragen und treibt das Boot in Windrichtung ab. Das alles richtig einschätzen zu können ist eine Kunst des Skippers. Man kann das nicht wirklich berechnen und die Wirkungen sind bei jedem Bootstyp verschieden. Werden mehrere Wenden gefahren, dann gleicht sich dieser Effekt sogar aus. Der Skipper oder Navigator wird z. B. bei Nordwind und einer Kompass-Ablesung von 280° einen Fahrkurs von 270° annehmen. Er hat in diesem Fall den Kompasskurs mit -10° beschickt. Letztendlich brauchen wir die Route über Grund und die entsteht nicht allein durch den Bootsantrieb. Abhängig vom Seegebiet können Meeresströmungen dazu beitragen, dass sich Geschwindigkeit und Kurs von den Anzeigen der Messgeräte an Bord ziemlich unterscheiden. Für eine möglichst genaue Koppelnavigation ist deshalb auch die Berücksichtigung einer Meeresströmung wichtig. Diese entnimmt man speziellen Strömungskarten. Besser ist jedoch die Benutzung eines Meeres-Strömungen-Radars das live Daten liefert. Dazu ist ein Internetzugang erforderlich. Fehlt dieser, dann könnte man jemanden anzurufen, der einem die Daten dann mitteilt. Bei Benutzung analytischer Navigationsmethoden kann die Zeitspanne zwischen zwei Beobachtungen etwas kürzer gehalten werden, weil diese einfach genauer rechnen. In strömungsarmen Gebieten entsteht dadurch kaum ein nennenswerter Fehler. Trotzdem soll nachfolgend die Berechnung einer gekoppelten Strecke unter Berücksichtigung von Meeresströmungen gezeigt werden.

Ein Schlag und zwei Geschwindigkeiten

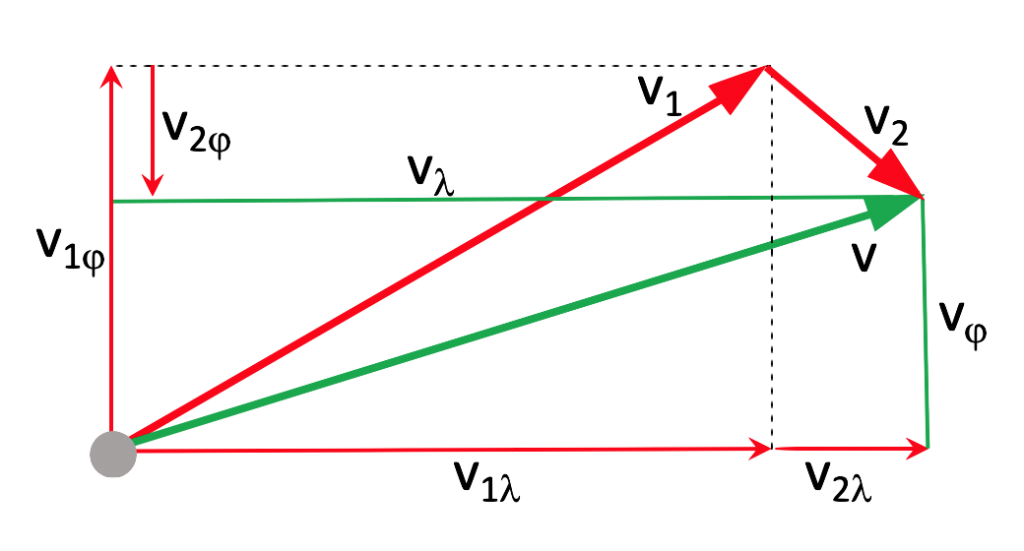
*Bild 1: Addition der Geschwindigkeitskomponenten Bootsantrieb und Strömung*

Ein Schlag ist definiert als eine gefahrene Strecke in einem bestimmten Kurs. Das bedeutet, dass ein neuer Schlag immer nach einer Wende, einer Halse, einer nachhaltigen Geschwindigkeitsänderung oder einer nachhaltigen Kursänderung beginnt. Auf die Länge der Distanz eines Schlages und auf den gefahrenen Kurs dieser Strecke nehmen der Bootsantrieb, aber auch die Stärke einer Strömung Einfluss.

Bild 1 zeigt den Zusammenhang. So findet die vom Bootsantrieb erzeugte Geschwindigkeit v1 durchs Wasser in einem Strömungsfeld statt, das mit der Geschwindigkeit v2 in eine andere Richtung driftet. Die dadurch resultierende Geschwindigkeit v wird dadurch erhalten, dass die beiden Vektoren v1 und v2 aneinander gesetzt werden. Der resultierende Kurs, auf dem sich das Boot dann bewegt hat, ist der Winkel zwischen der Nordrichtung v₁ und dem Geschwindigkeitsvektor v.

Die jeweiligen Distanzen sind die Produkte von Geschwindigkeit v und Zeitdauer t. Da man für eine Gesamtbewertung letztlich nur die Summe aller Nord-Süd Abschnitte und die Summe aller Ost-West Abschnitte braucht, egal wie viele Wenden oder Halsen gefahren wurden, müssen diese zunächst definiert werden. Mit dem Zählindex i für jeden Schlag, als i = 1 bis n, wenn n Schläge gefahren werden, gilt:

$\Delta\varphi_i=t_i\cdot (v_{Ai}\cdot\cos c_{Ai}+v_{ci}\cdot\cos c_{ci})$

$\Delta\lambda_i=t_i\cdot (v_{Ai}\cdot\sin c_{Ai}+v_{ci}\cdot\sin c_{ci})$

Hierin bedeuten:

i Nr. des gefahrenen Schlages
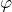∆ $\varphi$ _i Süd-Nord Komponente des gefahrenen Schlages in NM
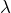∆ $\lambda$ _i West-Ost Komponente des gefahrenen Schlages in NM
t_i Zeitdauer des gefahrenen Schlages in h
v_Ai Geschwindigkeit durchs Wasser durch den Bootsantrieb in kn
c_Ai Kurs durchs Wasser auf dem gefahrenen Schlag in Grad
v_ci Geschwindigkeit einer aktuellen Meeresströmung in kn
c_ci Richtung einer Meeresströmung in Grad

Die Abschnitte werden jetzt getrennt addiert und man erhält die gesamt zurückgelegten Distanzen in Nord-Süd und in Ost-West Richtung:

$\Delta\varphi_T=\Delta\varphi_1+\Delta\varphi_2+\Delta\varphi_3+ ...\Delta\varphi_n=\sum_{i=1}^{n} \Delta\varphi_i$

$\Delta\lambda_T=\Delta\lambda_1+\Delta\lambda_2+\Delta\lambda_3+ ...\Delta\lambda_n=\sum_{i=1}^{n} \Delta\lambda_i$

Daraus kann jetzt mit dem Satz des Pythagoras die Distanz über Grund DMG berechnet:

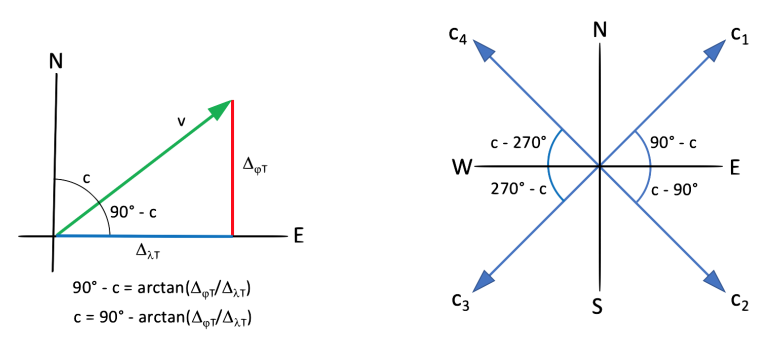
$DMG=\sqrt{(\Delta \varphi_T )^2+(\Delta \lambda_T )^2}$

Ein klein wenig komplizierter ist die Berechnung von CMG, weil dieser Winkel auf den Nordmeridian des Startpunktes bezogen werden muss. Dafür gelten zwei unterschiedliche Formeln, die davon abhängen, ob die zurückgelegte Strecke nach Osten oder nach Westen gesegelt worden ist:

$CMG=90^\circ-\arctan\frac{\Delta\varphi_T}{\Delta\lambda_T}\phantom{11}\text{wenn }\Delta\lambda_T>0$

$CMG=270^\circ-\arctan\frac{\Delta\varphi_T}{\Delta\lambda_T}\phantom{11}\text{wenn }\Delta\lambda_T<0$

Die Formeln sind am Bild 2 gut nachvollziehbar. In dem Dreieck auf der rechten Seite ist der Tangens des Winkels 90° – c der Quotient der Katheten, welche jeweils die Summen der gesegelten Nord-Süd und Ost-West Distanzabschnitte sind. Der Arcustangens ist dann der Winkel 90° – c selbst. Wenn der Abschnitt ∆ $\varphi$ _T negativ wird, also in südliche Richtung gesegelt wurde, dann ist auch der Arcusrangens negativ und damit erfolgt eine Vermehrung der vorgegebenen 90°. Wird in Richtung Westen gesegelt, muss mit 270° anstelle 90° gerechnet werden.

Aus dem Ergebnis von DMG und der zum Absegeln aller Schläge verstrichenen Zeit t_T, erhält man dann auch die VMG, die durch Kreuzen, Halsen, Geschwindigkeit- und Kurskorrekturen gesegelte Geschwindigkeit im Wind- und Strömungsfeld :

$VMG=\frac{DMG}{t_T}$

Beispielrechnung

Zum Schluss soll noch ein Beispiel folgen. Ein Segelboot fährt die im Bild 3 dargestellt Route. Sie besteht aus insgesamt vier Schlägen, wobei der zweite Schlag denselben Kurs verfolgt wie der erste, aber mit einer kleineren Geschwindigkeit, weil der Wind dauerhaft schwächer geworden ist.

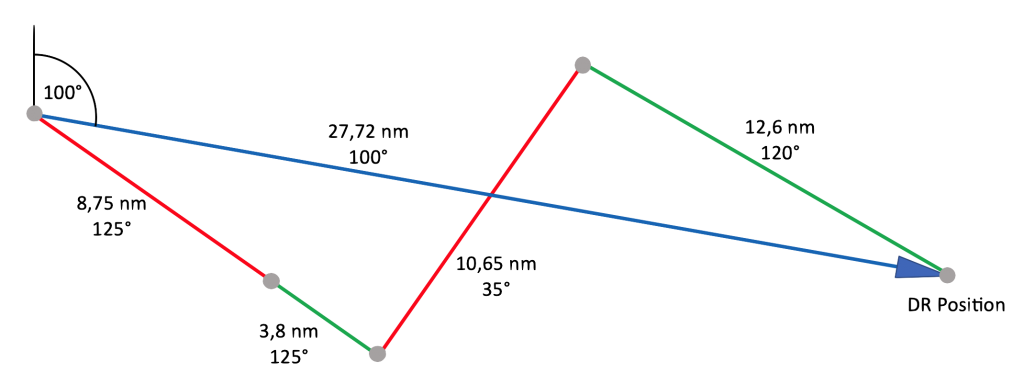
*Bild3: Darstellung der in der Tabelle gezeigten Schläge. Die dargestellten Distanzen sind die Produkte aus resultierender Geschwindigkeit und Zeit.*

Die einzelnen Schläge werden am besten in einer sogenannten Koppeltafel erfasst. Eine solche zeigen die unten stehenden Tabellen. In den ersten Spalten sind Fahrkurs, Boat Speed, Strömungsdaten und die Zeit eines jeden Schlages eingetragen. Die Ergebnisspalten geben dann Auskunft über die gesegelte Leistung als Distanz über Grund, Kurs über Grund und dabei erreichte Geschwindigkeit zum Abschluss eines jeden Schlages.

i	v_Ai kn	c_Ai deg	v_ci kn	c_ci deg	t	∆XXXXXXX_i NM	∆XXXXXXXXXXXXXXXX_i NM	∆XXXXXXXXXXXX_T NM	∆XXXXXXXXXXXXXXXXX_T NM	DMG NM	CMG deg	VMG kn
1	8,2	125°	0	0°	01:04	-5,02	7,16	-5,02	7,16	8,7	125	8,2
2	6	125°	0	0°	00:38	-2,18	3,11	-7,20	10,28	12,5	125	7,4
3	7,7	35°	0	0°	01:23	8,73	6,11	1,53	16,39	16,5	85	5,3
4	7	120°	0	0°	01:48	-6,30	10,91	-4,77	27,30	27,7	100	5,7

i	v_Ai kn	c_Ai deg	v_ci kn	c_ci deg	t	∆XXXXXX_i NM	∆XXXX_i NM	∆XXXXXXX_T NM	∆XXXXXXXXXXXXXX_T NM	DMG NM	CMG deg	VMG kn
1	8,2	125°	1	250°	01:04	-5,38	6,16	-5,38	6,16	8,2	131	7,7
2	6	125°	1	270°	00:38	-2,18	2,48	-7,56	8,64	11,5	131	6,8
3	7,7	35°	0,5	300°	01:23	9,07	5,51	1,51	14,15	14,2	84	4,6
4	7	120°	0,5	330°	01:48	-5,52	10,46	-4,01	24,61	24,9	99	5,1

Die Berechnungen leiden also nicht an Armut, sind aber elementar. Die Bezeichnung „Dead Reckoning“ (totale Berechnung) für eine Koppelnavigation ist also gar nicht so falsch. Man navigiert schließlich nur mit den Grunddaten Kompasskurs, Geschwindigkeit und Zeit einer Bootsbewegung unter Berücksichtigung von Strom und Windversatz. Jedes Wegstück, in dem sich auch nur einer der Einflußparameter geändert hat, muss als gesonderter Schlag betrachtet und berechnet werden. Erst die Addition aller dadurch gefundenen Schläge liefert dann den zurückgelegten Weg des Bootes über Grund. Es ist also eine ziemlich umfangreiche (totale) Rechnerei, wenn man analytisch vorgehen will, was heutzutage mittels eines Programms erledigt wird. In früheren Tagen wurde eine Koppelnavigation deshalb immer grafisch ausgeführt, was dann Bilder wie Bild 3 erzeugt.