Dass für eine Standortbestimmung mit der Sonne lange Zwischenzeiten überhaupt nicht notwendig sind, hat Herr Ralf Lampalzer im Jahre 1989 mit der Vorstellung seines Tagbogenverfahrens gezeigt. Das Verfahren ermöglicht eine Standortbestimmung in etwa 45 Minuten. Innerhalb einer ersten viertel Stunde erfolgen drei Messungen. Nach einer Pause von einer weiteren viertel Stunde Dauer folgen abschließend drei weitere Messungen. Daraus ergibt sich bereits ein recht sicherer Standort. Noch bessere Ergebnisse erhält man allerdings mit noch mehr Messungen. Herr Lampalzer beteiligte sich damals mit seinem Verfahren an dem Programm „Jugend forscht“ des Bundesministeriums für Bildung und Forschung und errang damit den Bundessieg.
Einfach erklärt, beobachtet das Verfahren eine relativ kurze Zeit der Höhenverlauf der Sonne und schließt daraus auf den globalen Standort des Beobachters.
Für die Berechnung der Höhe der Sonne über dem Horizont gilt folgende Gleichung:
(1) 
Darin enthalten sind zwei Unbekannte, nämlich 𝜑 und λ. Zur Lösung braucht es deshalb eine zweite Gleichung am selben Modell. Wenn Gl. 1 die Höhe einer ersten Beobachtung beschreibt, dann kann dieselbe Gleichung auch für eine zweite, später stattfindende Beobachtung aufgestellt werden. Diese lautet dann:
(2) 
Die beiden vorstehenden Gleichungen bilden ein Gleichungssystem mit den beiden Unbekannten 𝜑 und 𝜆, der Standortbreite und der Standortlänge. Das war genau der Ansatz, den Carl Friedrich Gauß vor mehr als 200 Jahren benutzte, um einen Standort mit einem Sextanten bestimmen zu können. Doch leider enthält das Gleichungssystem ausschließlich die transzendenten Funktionen sin(x) und cos(x) und ist deshalb nicht direkt lösbar. Möglich wäre eine numerische Auflösung, die jedoch mit einem großen Rechenaufwand verbunden ist. Gauß fand für seinen Ansatz einen analytischen Weg zur Lösung dieser Gleichungen.
Um die beiden Unbekannten 𝜑 und λ bestimmen zu können, brauchte Herr Lampalzer ebenfalls eine zweite Gleichung, was dann auf ein Gleichungssystem, bestehend aus zwei Gleichungen mit zwei Unbekannten führt.
Den Weg dahin fand er in der Anwendung der Methode der kleinsten Fehlerquadrate. Diese Methode ist dazu geeignet, eine Wolke von Messwerten dem Verlauf einer vorgegebenen Funktionsgleichung anzupassen. Wenn also eine Anzahl von n Messwerten vorliegt, dann wird folgendes definiert:
(3) 
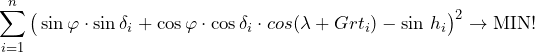
Die Summe aller Quadrate der Differenzen zwischen den gemessenen Höhen und der allgemeinen mit Gl. 1 definierten Höhengleichung soll ein Minimum sein. Mit dem Quadrat werden Messwerte mit größeren Abweichungen zur Zielfunktion stärker berücksichtigt.
Das Minimum einer mathematischen Funktion wird dadurch gefunden, dass ihre Ableitung, das ist ihre durch Differenzieren erhaltene Funktion, gleich Null gesetzt wird. Im vorliegenden Fall muss partiell einmal nach der Breite φ und einmal nach der Länge λ differenziert werden. Das führt dann auf die folgenden Aufgaben:
(4) 
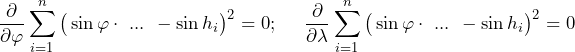
Die Ausführung dieser beiden partiellen Ableitungen, liefert dann das Gleichungssystem, bestehend aus zwei Gleichungen mit den zwei Unbekannten 𝜑 und 𝜆.
Leider enthält das Gleichungssystem ausschließlich die transzendenten Funktionen sin(x) und cos(x) und ist deshalb nicht analytisch lösbar. Da wir heute jedoch über Computer verfügen, bietet sich der Weg einer numerischen Lösung an.
Hier kann das Numerische Lösungsverfahren, der zweidimensionale Gradientenabstieg nach Newton, verwendet werden. Dabei wird mit einem Startwert begonnen und der Berechnungsprozess verbessert diesen Wert. Es ist also ein iteratives Lösungsverfahren. Nach mehreren Durchläufen des gleichen Rechenprozesses, der stets mit den jeweils verbesserten Ergebnissen startet, ist dann irgendwann die Lösung in den ersten 4 Stellen hinter dem Komma stabil.
Das Verfahren ermöglicht bei den typischen Messfehlern (Sextant freihändig gehalten, Seegang) von ca. 2′ eine für praktische Zwecke brauchbare Standortbestimmung in etwa 45 Minuten mit 10 Messungen.
Download unter www.Lampalzer.de > Downloads
Zwischenzeit
Zwischenzeit ist die Zeit zwischen zwei aufeinaderfolgenden Beobachtungen die bei einer Standortbestimmung mit nur einem Gestirn auftritt. Bei dem grafischen Interceptverfahren von Saint Hilaire folgt der Standort aus zwei sich kreuzenden Bleistiftlinien. Dabei dürfte dann klar sein, dass sich diese Linien in einem möglichst stumpfen Winkel schneiden sollten. Als gerade noch ausreichend werden dabei 30° erachtet. Dafür ist dann eine Zwischenzeit von wenigstens zwei Stunden nötig.
Bei analytischen Verfahren zur Standortbestimmung wird nicht mit Standlinien gearbeitet, sondern direkt mit den Höhenkreisen. Auch dabei ergeben sich die möglichen Standorte aus den Schnittpunkten, die sich aus den Überlappungen zweier Höhenkreise ergeben. Diese Überschneidungen können spitzwinklig oder stumpfwinklig ausfallen.
Tests mit der Gauß Methode haben gezeigt, dass ein Standort auch dann noch fehlerfrei berechnet wird, wenn die Zwischenzeit nur 5 Minuten lang ist. Vorausgesetzt, die eingegebenen Höhen sind absolut fehlerfrei. Ein weiteres Ergebnis zeigt, dass die Fehlertoleranz mit größer werdender Zwischenzeit zunimmt. Mit anderen Worten, ist die Zwischenzeit kurz, dann müssen die Höhenmessungen sehr genau sein. Lange Zwischenzeiten tolerieren Höhenmessfehler viel besser.
In welchem Maße diese Feststellung auch für das hier vorgestellte Tagbogenverfahren gilt, wurde noch nicht untersucht. Festgestellt wurde bisher nur, dass auch hier eine große Zwischenzeit toleranter gegenüber fehlerbehafteten Höhenmessungen ist.