Zur Bestimmung des Breitenkreises, auf dem sich ein Schiff gerade befindet, entwickelte der Mensch zahlreiche Werkzeuge, mit denen er diejenigen Himmelskörper beobachten konnte, die ihm Aufschluss darüber gaben. Die wichtigsten waren der Jakobsstab, Quadrant, Oktant und schließlich der Sextant. Seit langem schon war bekannt, dass die Höhe des Nordsterns auf der Nordhalbkugel mit der Standortbreite ziemlich gut übereinstimmt und seit dem Mittelalter existieren einigermaßen brauchbare Deklinationstabellen, die es ermöglichen, die Standortbreite auch aus der Kulmination der Sonne am Mittag zu bestimmen. Daraus entwickelte sich schon früh eine besondere Navigationsmethode, das sogenannte Breiteln.

**Bild 1.1 links: Die Beobachtung der Sonne mit einem Jakobsstab führte oft zu Erblindungen. Bild 1.2 rechts: Mit einem Oktanten wurden genauere Beobachtungen möglich.**

Auch Columbus hat diese Methode benutzt, um zurück nach Europa zu kommen. Er segelte zunächst von der Karibik kommend immer nur nach Nordosten, bis er die gewünschte Breite von Kap St. Vincent in Portugal erreichte, und änderte dann seinen Kurs direkt nach Osten. Auf seiner Weiterreise versuchte er, auf möglichst gleicher Nordsternhöhe zu bleiben, auch wenn ihn manchmal Stürme abtrieben. Im Verlauf seiner Reise traf er auf die Azoren und erreichte schließlich sogar ziemlich genau Lissabon, was am Ende mehr ein Zufall war.

Eine Bestimmung des Längengrades galt dagegen lange Zeit als unmöglich, obwohl bereits Wege dafür angedacht waren. Im 16. Jahrhundert vertraten Galilei und andere die Auffassung, dass der Längengrad mit einer exakt laufenden Uhr bestimmt werden könne. Doch der Versuch einer Längengrad-Bestimmung mit einer Pendeluhr an Bord dauerte nur bis zum ersten Sturm, der das Pendel völlig außer Takt brachte und nach dem die Uhr dann nicht mehr gestellt werden konnte.

Später ermittelte man die Zeit durch Messungen von Monddistanzen zu Fixsternen, die wiederum eine Bestimmung der Zeit in Greenwich ermöglichten. Spätestens damit erlangte die Mathematik einen wichtigen Stellenwert in der Praxis der Navigation.

1.1 Das Problem der der zwei Höhen

Der Portugiese Pedro Nunes (1502–1578) beschrieb ein Prinzip, wonach die geografische Breite aus zwei unterschiedlichen Höhen der Sonne bestimmt werden kann. Von dem dänischen Astronomen Tycho Brahe (1546–1601) ist bekannt, dass er die unbekannte Position eines Sterns aus der bekannten Position zweier anderer Sterne ableiten konnte. Diese Aufgabe unterscheidet sich genau genommen nicht von der Bestimmung der unbekannten Position eines Schiffes. Das Gradnetz der Erde ist eine Projektion des Gradnetzes an der Himmelskugel. Somit ist die Position des Zenits Z eines Schiffes auf dem Gradnetz der Himmelskugel identisch mit der Position des Schiffes auf dem Gradnetz der Erde.

Auf diese Weise ließe sich die Tätigkeit der Astronomen auf eine Positionsbestimmung auf dem Meer übertragen. Die Aufgabe bestände nur darin, den unbekannten Zenit einer Schiffsposition aus der Position zweier bekannter Himmelskörper oder der Position der Sonne zu zwei verschiedenen Zeiten abzuleiten. Diese Aufgabe ist als Problem der zwei Höhen oder einfach als Zweihöhenproblem bekannt geworden.

Ein einfacher Rechenweg ließ sich für diese Aufgabe allerdings nicht finden. Die Mathematik befand sich noch im Wachsen. Zwar gab es schon genügend Arbeitsergebnisse zur sphärischen Trigonometrie, doch diese waren noch völlig ungeordnet und damit nicht reif für eine allgemeine Verwendung. Einen Anschub zur Lösung des Zweihöhenproblems leistete ein Preisausschreiben, das die Pariser Akademie der Wissenschaften am 17. Mai 1727 veröffentlicht hatte. Ein Preis sollte demjenigen zuerkannt werden, der eine praktikable Lösung für das Zweihöhenproblem anbieten konnte. Unter den zahlreichen Teilnehmern, die einen Preis zu gewinnen hofften, fand sich auch Daniel Bernoulli, der heute vor allem als Begründer der Strömungslehre bekannt ist. Er wollte die geografische Breite aus drei aufeinanderfolgenden Höhenmessungen und den korrespondierenden Zwischenzeiten an einem und demselben Himmelskörper bestimmen, ohne dessen Koordinaten kennen zu müssen.

Die Suche nach einfachen Lösungen zog sich recht erfolglos bis fast in die Mitte des 19. Jahrhunderts hin. Unzählige Publikationen mit mehr oder weniger praktischem Nutzen wurden bekannt. Vielfach wurde versucht, die sphärische Trigonometrie zu umgehen, indem stattdessen in der Trigonometrie der Ebene oder sogar in der allgemeinen Arithmetik nach Ausweichlösungen gesucht wurde.

In der zweiten Hälfte des 18. Jahrhunderts hat Leonhard Euler (1707–1783) die Sätze der sphärischen Trigonometrie systematisiert und darüber hinaus leicht verständliche Anleitungen gegeben, wie diese anzuwenden sind. Weil zu dieser Zeit die Berechnung nur mithilfe von Logarithmen möglich war, hat Euler die Formeln sogar in zwei Varianten publiziert. In einer ersten Variante wurden sie in ihrer anschaulichsten und heute üblichen Form dargestellt. Die zweite Variante war eine sogenannte abgeleitete Gleichung, die nur noch aus Produkten und Quotienten bestand, und damit im Hinblick auf eine rechnerische Anwendung mit Logarithmen optimiert war. Mit dieser Arbeit hatte Euler die Grundlage für ein mathematisch strenges Verfahren zur Berechnung der Breite eines Standortes aus den gemessenen Höhen zweier Himmelskörper geschaffen.

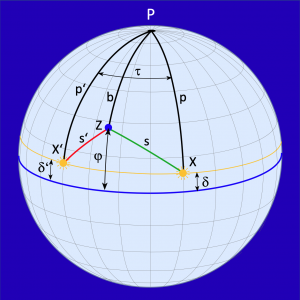
***Bild 1.3: Zweihöhenproblem: Bestimmung des Standortes Z aus den Deklinationen und Höhen der Sonne aus zwei Zeiten.***

Nachfolgend soll der mathematische Hintergrund der Lösung des Zweihöhenproblems dargelegt werden. Wir benutzen dazu die Skizze im Bild 1.3. Darin finden wir die Zenitalpunkte bzw. Bildpunkte der Sonne, die mit X und X’ bezeichnet sind. Das sind die geografischen Punkte auf der Erde, an denen die Sonne gerade im Zenit steht – und zwar zu dem Zeitpunkt, in dem ihre jeweilige Höhe über dem Horizont von einem Standort Z aus mit einem Sextanten gemessen wird. Die geografischen Positionen dieser Bildpunkte in den Messzeiten müssen natürlich bekannt sein. Dafür gab es damals schon Tabellen, aus denen die Deklinationen 𝛿 für jede Stunde eines Jahres entnommen werden konnten. Die Beobachtungszeiten sollten ein paar Stunden Sonnenlaufzeit auseinanderliegen, und zudem war es günstig, die erste Beobachtung am Vormittag und die zweite am Nachmittag zu machen. Einen vierten Bezugspunkt in diesem Modell stellt der Pol P dar, der in unserem Fall der Nordpol ist.

Die Längen zwischen den Punkten X und P bzw. X’ und P sind bekannt. Sie errechnen sich mit 90° – 𝛿 bzw. 90° – 𝛿’. Ebenso bekannt sind die Längen zwischen den Punkten X und Z bzw. X’ und Z, denn das sind die Zenitabstände der gemessenen Sonnenhöhen, und zwar s = 90° – h bzw. s’ = 90° – h’. Diese Längen und ebenso p bzw. p’ sind die Komplemente der Deklinationen und gemessenen Höhen der Sonne. Komplemente sind Ergänzungen von Winkeln zu 90°. Daraus ergeben sich zwei nebeneinander liegende sphärische Polardreiecke. Diese haben eine gemeinsame Seite, nämlich die Seite b. Sollte es jetzt gelingen, diese Seite b zu berechnen, dann hätte man die Standortbreite 𝜑, denn auch hier gilt die Komplement-Beziehung 𝜑 = 90° – b.

Eine letzte exakte Beschreibung des auszuführenden Rechenweges zur Bestimmung der Breite 𝜑 ist als Ergebnis einer Zusammenarbeit des Niederländers Pieter Nieuwland mit Franz Xaver von Zach (2) in Gotha im Jahr 1792 bekannt geworden. Dieser wird auf Seite 92 im Kapitel 4.3.1 ausgeführt. Es war der ernüchternde aber zugleich perfekte Höhepunkt einer 250 Jahre andauernden Suche nach einer Lösung des Zwei-Höhen-Problems. Perfekt deshalb, weil kein besserer geometrischer Weg denkbar war und ernüchternd, weil eine Lösung mithilfe von Logarithmentafeln zu aufwendig und deshalb zur Benutzung an Bord eines Schiffes nicht infrage kommen würde.

1.2 Cornelis Dowes

Die astronomische Aufgabe, die Breite eines Ortes zu finden, galt damals als eine der wichtigsten in der Geografie und Navigation. War von einem Schiffsort die Breite bekannt, so konnten aus gemessenen Distanzen zwischen Mond und bekannten Fixsternen die Zeit und damit die geografische Länge sowie daraus der Standort bestimmt werden. Die Monddistanzen-Methode war allerdings auch nicht ganz trivial und erforderte neben einigen Berechnungen zudem noch Unterlagen in Form von astronomischen Tabellen. Die exakte Breite war bis dato deshalb nur aus der Beobachtung des Nordsterns oder als Mittagsbreite zu bestimmen.

Der Holländer Cornelis Douwes (1712–1773) war Direktor der Seefahrtschule in Amsterdam. Seine Vision war es, das Zweihöhenproblem für die Seefahrer nutzbar zu machen. Zu diesem Zweck entwickelte er eine Methode, wie aus zwei außer dem Mittagskreis beobachteten Sonnenhöhen die Breite eines Ortes gefunden werden kann. Sein Ansatz bestand darin, die mühsame logarithmische Berechnung der Polardreiecke abzukürzen, indem er eine spezielle eigene Logarithmentafel schuf. Bei Benutzung dieser Douw’schen Tafel musste weniger gerechnet und weniger in Tabellen gesucht werden. Insgesamt waren neun Tabellenzugriffe für eine Breitenberechnung erforderlich. Dies verringerte den Rechenaufwand gegenüber der strengen Rechenmethode mit mehr als 20 notwendigen Tabellenzugriffen, wobei nach jedem Tabellenzugriff auch immer eine Interpolation nötig war, auf etwa ein Drittel. Seine Methode war nicht ganz exakt und enthielt Vereinfachungen. Eine davon war die Notwendigkeit, einen Standort vorher schätzen zu müssen.

Douwes erhielt für seine Tafelmethode von der britischen Längengradkommission einen ansehnlichen Preis. Danach hat sich sein Verfahren sowohl unter den niederländischen als auch englischen Seeleuten etablieren können und war bis ins 19. Jahrhundert hinein eine verbreitete Navigationsmethode.

1.3 Chevalier de Borda

Eine außerordentlich interessante Idee zur Breitenbestimmung hatte der Franzose Jean Borda auf seiner Reise 1771/72, die ihn mit dem Forschungsschiff Flora an der westafrikanischen Küste entlangführte. Genaue Ergebnisse konnte man damit allerdings nur über sogenannte rigorose Berechnungen erhalten.

Borda machte zwei Beobachtungen der Sonne, um deren Höhen h und h’ über dem Horizont feststellen zu können. Sein Prinzip wird mit Hilfe von Bild 1.4 deutlich. Die erste Messung erfolgt beispielsweise am Vormittag und liefert den grün markierten Horizontabstand s = 90° – h. Die zweite Beobachtung am Nachmittag zeigt dann den im Bild rot markierten Horizontabstand s’ = 90° – h’.

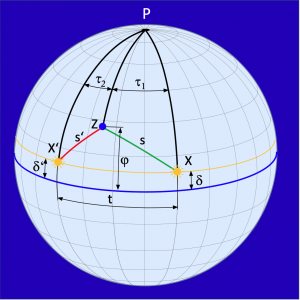
***Bild 1.4: Borda: Diejenige Breite ist die Richtige, bei der die Zwischenzeit t mit der Summe der aus den Stundenwinkeln berechneten Zeit übereinstimmt.***

Das Verfahren ist besonders dann geeignet, wenn die Mittagsbreite wegen einer Bedeckung des Himmels nicht bestimmt werden kann. Neben den Höhenmessungen musste auch die Zwischenzeit t, die Zeit zwischen den Beobachtungen, festgehalten werden, die jedoch mit einer einfachen Schiffsuhr gemessen werden konnte.

Vor dem Beginn einer Berechnung musste die eigene Breite 𝜑 noch geschätzt werden. Aus dieser geschätzten Breite, den Komplementen s und s’ aus den jeweils beobachteten Höhen und den Deklinationen 𝛿 und 𝛿’ während der Beobachtungszeiten wurden dann die Stundenwinkel 𝜏1 und 𝜏2 der beiden Polardreiecke XPZ und X’PZ berechnet.

Diese wurden addiert und ihre Summe durch die Winkelgeschwindigkeit der Sonne von 15°/h dividiert. Das Ergebnis davon war die berechnete! Laufzeit der Sonne zwischen den Beobachtungen. Diese würde mit der gemessenen Zwischenzeit t übereinstimmen, wenn die Breite richtig geschätzt worden wäre.

Auf dem Bild ist leicht nachvollziehbar, dass sich der Abstand zwischen den Bildpunkten der Sonnen X und X’ spreizt, wenn bei gleichbleibenden Längen von s und s’ eine kleinere Breite zur Anwendung kommt bzw. geschätzt wird. Als Folge würde dann eine Laufzeit der Sonne berechnet werden, die größer ist als die gemessene wahre Zwischenzeit t.

Nun könnte das Ganze mit einer jeweils anderen Breite wiederholt werden, bis es passt. Der Astronom Jerome Lalande hatte dann allerdings die Idee, die wahrscheinlich richtige Breite aus zwei Breitenschätzungen über einen Dreisatz zu finden. Das Verfahren erwies sich als bemerkenswert genau, wenn es gelang, die Breiten vorher einigermaßen exakt zu schätzen. War dies nicht der Fall, dann ergaben sich größere Abweichungen, die zur Wiederholung der ganzen Rechnungen drängten. Die Standortlänge bekam man aus der Zeit, die damals allerdings nur über Monddistanzen zu bekannten Fixsternen ermittelt werden konnte.

Auch dieses Verfahren erforderte mitunter einen riesigen Rechenaufwand und so kam es bei den Seefahrern ebenfalls nicht an

1.4 Die Chronometerlänge

***Bild 1.5: Die H4, die vorletzte von John Harrison gebaute Längengraduhr.***

Mit einem ersten Uhr-Exemplar von Harrison, das später den Namen H1 bekam, gelang eine Testfahrt, bei der die Genauigkeit der Methode bestätigt werden konnte. Das Preisgeld wurde jedoch nicht gezahlt, weil die Testreise nicht ganz den Anforderungen entsprach. Es könnte auch alles nur Zufall gewesen sein, meinten einige Kritiker. Außerdem gab es Widerstände und Bedenkenträger. So wurde die Zuverlässigkeit eines technischen Instrumentes grundlegend angezweifelt.

Ein ständiger Widersacher war insbesondere der Hofastronom des englischen Königshauses, Nevil Maskelyne. Er setzte auf die Monddistanzmethode, weil diese unabhängig von technischen Instrumenten ist. Zudem sah er in der Entwicklung der Längenuhr eine Konkurrenz zu seinen eigenen Ideen, mit denen er die Monddistanzmethode vervollkommnen wollte.

Erst als James Cook 1775 von seiner zweiten Weltreise zurückkehrte und die gute Qualität eines heute mit K1 bezeichneten Modells eines Harrison Chronometers bestätigte, galt auch in Astronomen-Kreisen das Längenproblem als gelöst. Harrison wurde ein Preisgeld von 10 000 £ zugesprochen. Die K1 war ein exakter Nachbau der H4. Eine Weiterentwicklung, heute mit H5 bezeichnet, wurde von König Georg III persönlich getestet. Der Test verlief erfolgreich und Harrison erhielt weitere 8 750 £.

Nach dem Erfolg der H5, die damals etwa 500 £ kostete, bauten Uhrmacher die Modelle nach und die Preise sanken. Die ersten in Serie produzierten Marine Chronometer waren ab etwa 1790 verfügbar. Die Tatsache, dass die Beagle auf ihrer Forschungsreise mit dem berühmten Charles Darwin gleich 22 Stück an Bord hatte, zeigt, welche Bedeutung sie plötzlich bekamen. Erst gegen Ende des . Jahrhunderts konnte der Bedarf an Chronometern einigermaßen gedeckt werden – in England bereits früher.

Die Bestimmung der Chronometerlänge ist ein einfacher Vorgang, den wir uns nun an dem im Bild 1.6 aufgezeigten Modell klarmachen wollen. Nachdem die Breite 𝜑 z. B. als Mittagsbreite oder Koppelbreite festgestellt worden ist, wird die Höhe der Sonne über der Kimm mit einem Sextanten gemessen. Nach Berichtigung des abgelesenen Höhenwinkels erhält man die beobachtete Höhe h. Das Komplement dieser Höhe, die Ergänzung zu 90° ist der Zenitabstand s, der im Bild als die grüne Dreieckseite zwischen Z und X eingezeichnet ist. Ganz entscheidend bei Höhenmessungen ist die Feststellung der sekundengenauen Zeit, in der das Gestirn im Teleskop des Sextanten auf die Kimm gesetzt wurde.

Als Nächstes muss die Deklination 𝛿 aus einem nautischen Almanach herausgesucht werden. Dazu braucht man ebenfalls die Beobachtungszeit, jedoch nur minutengenau, weil sich die Deklination nur sehr langsam ändert.

Damit sind alle Seiten des nautischen Dreiecks bzw. Poldreiecks im Bild 1.6 bekannt. Wir haben also:

Seite b = 90° – 𝜑,
Seite s = 90° – h,
Seite p = 90° – 𝛿.

Wenn von einem sphärischen Dreieck die Längen aller Seiten bekannt sind, dann kann jeder der drei möglichen Winkel berechnet werden. In unserem Fall wird der Polwinkel 𝜏 berechnet.

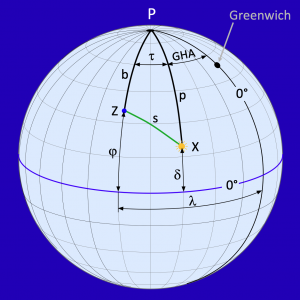
***Bild 1.6: Bestimmung der Chronometerlänge an einem Polardreieck als Summe (oder Differenz) von GHA (Grt) und Stundenwinkel. (s = 90° – h)***

Die Länge 𝜆 besteht, wie im Bild zu sehen ist, aus der Summe von 𝜏 und einem zweiten mit GHA bezeichneten Winkel. GHA ist die Abkürzung für Greenwich Hour Angle. Im deutschen Sprachgebrauch ist dafür die Bezeichnung Grt üblich. Dieser bis 360° gehende Stundenwinkel ist die Differenz zwischen dem durch die Sternwarte von Greenwich laufenden Nullmeridian und dem Meridian, auf dem der Bildpunkt der Sonne in einer anzugebenden Zeit, üblicherweise der Beobachtungszeit, steht. Diese Zeit muss sekundengenau angegeben werden, denn die Winkelgeschwindigkeit der Sonne ist mit 15°/h sehr hoch. Am Äquator kann sie bis 463 m/s betragen.

Dass der Nullmeridian durch die Sternwarte von Greenwich gehen soll, wurde 1884 auf der internationalen Meridiankonferenz in Chicago beschlossen. Zuvor gab es mehrere Vorschläge, u. a. auch von Frankreich, den Nullmeridian durch Paris laufen zu lassen. Weil zu jener Zeit die größere Menge an bereits vorhandener nautischer Literatur und auch astronomischen Tafeln den Nullmeridian durch Greenwich berücksichtigten, fiel die Entscheidung auf diesen Ort.

Doch nun wieder zu Sache. Mit der bekannten Zeit der Höhenmessung und der konstanten Winkelgeschwindigkeit der Sonne von 15°/h könnte jetzt der GHA berechnet werden, wenn die Zeit bekannt wäre, in der die Sonne den Nullmeridian passiert. Doch hier gibt es ein Problem.

Ein Chronometer geht absolut gleichmäßig. Wenn es 365-mal im Jahr seine 24 Stunden abdreht, dann geschieht es allerdings nur an vier Tagen, dass die Sonne genau um 12:00:00 GMT (Greenwich Mean Time – Zone), auf dem Nullmeridian kulminiert. An allen anderen Tagen kulminiert sie bereits vor 12:00 Uhr oder danach. Die Sonnenzeit und die Chronometerzeit laufen nämlich nicht synchron. Dies ahnte man bereits im Mittelalter und es hat sich später auch herausgestellt, dass die ersten genauen Pendeluhren nicht im Gleichgang mit den Sonnenuhren waren, die überall an den Kirch- oder Rathauswänden angebracht waren. Sie gingen scheinbar einmal vor und dann wieder nach.

Wenn mit der Sonne navigiert werden soll, dann muss auch die Sonnenzeit verfügbar sein. Um aus der Chronometerzeit die Sonnenzeit zu erhalten, brauchte man eine Korrektur- oder Ausgleichszeit. Der Name dafür lautet Zeitgleichung. Dies ist also keine Gleichung im mathematischen Sinne, sondern ein Wert aus einer Tabelle, der für ein bestimmtes Datum den Zeitausgleich schafft. Es sind tatsächlich bis zu 16 Minuten, die ein Chronometer innerhalb eines Jahres gegenüber der Sonnenzeit vor- oder nachgehen kann.

Nachdem Johannes Keppler die Bahn der Erde um die Sonne genau berechnet hatte, konnte auch die Zeitgleichung ermittelt werden. Diese Arbeit hat der erste Hofastronom des englischen Königshauses, John Flamsteed (1646–1719), durchgeführt. Demnach ist die von gleichmäßig gehenden sogenannten Räderuhren angegebene Zeit nur eine mittlere Zeit. Die wahre Sonnenzeit, die ein Navigieren mit der Sonne erst ermöglicht, ist die Summe von Chronometerzeit, die der GMT oder der Universalzeit UTC entspricht und der Zeitgleichung. An Bord der Schiffe musste deshalb neben einem genau gehenden Chronometer auch stets eine Jahrestabelle mit der Zeitgleichung vorhanden sein.

Um jetzt auf die Bestimmung des GHA zu kommen, stelle man sich vor, dass auf einem Schiff im Atlantik die Sonne um 14:00:00 GMT beobachtet wurde. Gemäß der Zeitgleichung soll die Sonne den Nullmeridian bereits um 11:52 GMT passiert haben und ist deshalb um 12:00 GMT schon 2° westlich von Greenwich. Damit ist dann klar, dass auch das Schiff um 14:00 GMT nicht auf 30° W, sondern auf 32° westlicher Länge steht.

So muss zur Bestimmung des Längengrades zunächst die Differenz zwischen Beobachtungszeit und 12:00:00 GMT berechnet werden. Dann wird die Zeitgleichung dazu addiert und die erhaltene Summe mit der Winkelgeschwindigkeit der Sonne von 15°/h multipliziert.
Ab Mitte des 19. Jhd. wird der GHA in Nautischen Jahrbüchern tabelliert, wodurch sich die Arbeit mit den Zeitgleichungstabellen erübrigt hat.

Bild 1.6 zeigt den Fall, dass die Sonne im Osten beobachtet wird, also am Schiffsvormittag. Dadurch errechnet sich die Standortlänge als Summe von GHA und 𝜏. Sobald die Sonne den eigenen Standortmeridian überholt hat, X also westlich von Z steht, muss die Standortlänge als Differenz von GHA und 𝜏 berechnet werden.

1.5 Carl Friedrich Gauß

Gauß war der wohl größte Mathematiker aller Zeiten. Im Zusammenhang mit einer seiner Lieblingsbeschäftigungen, der Landesvermessung und Kartografie, hat er sich auch mit der Bestimmung von Breiten- und Längengraden beschäftigt. Darüber hat er eine bemerkenswerte Arbeit verfasst, die nach ihrer Publikation im Jahre 1812 nie wieder in der nautischen Literatur Erwähnung gefunden hat. Bemerkenswert ist, dass der populäre Mathematiker und Buchautor Heinrich Dörrie (1873–1955) in seinem Fachbuch über die Trigonometrie unter der Überschrift „Gauß und das Zweihöhenproblem“ ein Verfahren als Gauß-Methode vorstellte, das gar nicht von Gauß stammt. Mehrere Autoren haben diesen Irrtum dann weiterverbreitet und die wahre Gauß-Methode umgedeutet.

Auch wenn Gauß kein Seemann gewesen ist, waren neben der Mathematik, der Astronomie und Kartografie nur zwei Gebiete unter vielen, in denen er außergewöhnliche Leistungen vollbrachte. Am bekanntesten ist wohl die von ihm gefundene Glockenkurve der statistischen Normalverteilung. Weitere bedeutende Arbeiten sind der nach ihm betitelte Gauß’sche Algorithmus zur Lösung algebraischer Gleichungssysteme oder die Methode der kleinsten Fehlerquadrate, mit der er z. B. die Bahn des Zwergplaneten Ceres berechnen konnte, sodass man ihn wiederfand, nachdem er eines Tages scheinbar hinter der Sonne verschwunden schien.

Als Kartograf musste Gauß auch Längen- und Breitengrade bestimmen können, um diese auf den Karten eintragen zu können. Dies war also nicht nur eine Aufgabe der Seefahrer. Das Problem der zwei Höhen und die Berechnung der Breite über die zwei Polardreiecke, wie sie im Bild 1.3 dargestellt sind, waren ihm wohlbekannt. Zur Lösung dieser Aufgabe sind mit Formeln aus der sphärischen Trigonometrie Stück für Stück einzelne Elemente des Grafikmodells auszurechnen, bis schließlich die Strecke b ermittelt werden kann, deren Ergänzung zu 90° die gesuchte Breite liefert.

Diese Aufgabe müsste aber auch anders lösbar sein. So kann die im Bild 1.3 gezeigte Grafik auch abstrahiert werden. Dazu werden die beiden Dreiecke nicht gezeichnet, sondern jeweils durch eine mathematische Gleichung ausgedrückt. Die Gleichungen hängen dann über ihre gemeinsame Seite b und einen Stundenwinkel zusammen. Das ist dann ein Gleichungssystem mit den zwei Unbekannten b und dem zwischen X und dem Standort Z bestehenden Stundenwinkel. Diese Idee hatte zuerst ein Mathematiker Namens Kraft. Seine Lösung war allerdings sehr verwickelt, und Gauß meinte dazu, dass stattdessen eine Lösung mithilfe der sphärischen Trigonometrie über die Dreiecke weit einfacher wäre.

Das Gleichungssystem besteht ausnahmslos aus den transzendenten Funktionen des Sinus und des Kosinus und es existiert kein Algorithmus bzw. allgemeiner Weg, diese Aufgabe überhaupt lösen zu können. Gauß fühlte sich jedoch herausgefordert und fand trotzdem einen Weg. Seine Methode war jedoch kaum vermittelbar, weil sie ein Sonderweg ist. Seine Analyse kann als Ergebnis eines wissenschaftlichen Streits mit Herrn Kraft gesehen werden. Das war also hochkarätige Mathematik, mit der kein Seemann hätte arbeiten können. Selbst wenn das gemacht worden wäre, der Aufwand gegenüber einer trigonometrischen Berechnung über die Dreiecke wäre nicht entscheidend kleiner geworden.

Heute, fast 200 Jahre später, verfügen wir über Computer, und denen ist es egal, ob die Formeln von Menschen verstanden werden oder nicht. Sie müssen nur richtig sein. Verpackt in einem Computerprogramm, ist die Gauß Methode ein ideales Navigationsmodul. Auch die Satellitennavigation funktioniert so. Ein Standort wird auf direktem Wege und nur durch Berechnung gefunden.

1.6 Die Industrielle Revolution

Sie begann in der zweiten Hälfte des 18. Jahrhunderts und nahm im 19. Jahrhundert an Fahrt auf. Technik, Produktivität und Wissenschaften beschleunigten sich. Seemacht und Seehandel wuchsen in einem bisher nie gekannten Maße. Segelschiffe mussten den neuen Dampfschiffen weichen. Für die Industrienationen lagen die Kolonien weit weg und eine ständig wachsende Bevölkerung in Europa sowie den vereinigten Staaten von Amerika wollte versorgt werden. Der zunehmende Schiffsverkehr auf den Weltmeeren litt sehr darunter, dass die Möglichkeiten einer sicheren Hochseenavigation nur äußerst begrenzt waren. Neben der Option einer Navigation mittels Mittags- oder Nordsternbreite und Bestimmung der Chronometerlänge stand zur Breitenbestimmung außerhalb der Mittagszeit nur das Douwessche Verfahren zur Verfügung. Die Hersteller von Chronometern bemühten sich sehr darum, den riesigen Bedarf der Reeder und Kapitäne zu befriedigen.

Um Zeit und damit Geld zu sparen, mussten die Schiffe schneller werden. So erreichten die legendären Klipper bei gutem Wind Etmale von mehr als 400 nautischen Meilen, was bedeutete, dass diese Schiffe mit Spitzengeschwindigkeiten von mehr als 20 Knoten fahren konnten. Trotz enormer Verbesserungen der Techniken und Ladefähigkeiten der Klipper konnten sie sich gegenüber Dampfschiffen am Ende dennoch nicht behaupten. Dampfschiffe verbrauchen jedoch Brennstoff, der Geld kostet. Wenn weniger Kohle gebunkert werden muss, dann kann mehr Nutzlast transportiert werden. Die gefahrenen Kurse wurden optimiert. Sie sollten dann aber auch eingehalten werden, was wiederum nur möglich werden konnte, wenn die Kapitäne entsprechende Navigationsmöglichkeiten an die Hand bekämen.

Der Druck, endlich bessere Navigationsverfahren zu entwickeln, wuchs. Die Mathematiker kannten zwar exakte Lösungen und das schon lange, aber der dafür zu leistende Rechenaufwand war an Bord der immer schneller werdenden Schiffe nicht zu erbringen. An Rechenhilfsmitteln standen nur Logarithmentafeln zur Verfügung. Damit hätte eine Standortberechnung viel zu lange gedauert. Außerdem wären gar nicht so viele Mathematiker aufzutreiben gewesen, um die Flotten damit zu bemannen.

In dieser Situation nahmen die Praktiker das Heft des Handelns selbst in die Hand. Der amerikanische Handelskapitän Thomas H. Sumner gilt als der Erfinder der Standlinie und begründete damit die grafischen Navigationsmethoden. Drei Jahrzehnte später gelang es dem französischen Fregattenkapitän Marcq Saint Hilaire, die Standlinienmethode entscheidend zu verbessern. Die Verbreitung der grafischen Methoden gilt als Wendepunkt in der Hochseenavigation sowie als Beginn der Ära der modernen Astronavigation, die erst mit der Einführung der Satellitennavigation ein Ende fand.

1.7 Grafische Navigation

Der Beginn der grafischen Navigation bedeutete in der weltweiten Seefahrt eine Zäsur. Endlich konnten Standorte auf See auch außerhalb der Mittagszeit bestimmt werden oder auch sofort über die Bestimmung der Höhe zweier bekannter Sterne. Die Ära der grafischen Navigation endete mit der Inbetriebnahme des ersten Satellitennavigationssystems GPS.

1.7.1 Thomas Sumner

Thomas Hubbard Sumner wurde 1807 als Sohn eines Architekten in Boston, Massachusetts geboren. Im Alter von 15 Jahren begann er ein Studium an der Harvard Universität, das er vier Jahre später abschloss. Im Jahr 1829 heuerte er als Seemann auf einem Handelsschiff auf der China Route an. Acht Jahre später war er Kapitän mit einem eigenen Schiff. Sumner hatte eine gute Ausbildung und verfügte über weitreichende Kenntnisse in Mathematik und Astronomie.

Am Morgen des 17. Dezember 1837 näherte sich Kapitän Sumner, er war schon 22 Tage von South Carolina kommend auf See, dem St. George Kanal zwischen Irland und Wales. Seine Reise ging nach Greenock in Schottland. Es stürmte und der Himmel war bedeckt. Er brauchte jetzt dringend Sicherheit darüber, dass ihn der Wind aus SSE nicht zu weit an die gefährlich flache und steinige Südostküste von Irland versetzt hatte. Etwa um 10:15 riss die Wolkendecke plötzlich auf und die Sonne wurde sichtbar. Dies reichte gerade für eine Messung des Kimmabstandes der Sonne.

Die Methoden zur Bestimmung der Mittagsbreite und der Chronometerlänge waren seit Beginn des 19. Jahrhunderts auf vielen Seeschiffen gut etabliert. Eine Längenbestimmung zur Mittagszeit ist damit allerdings nicht möglich. Auf ihrer Kulminationshöhe beschreibt die Sonne einen sehr flachen Bogen und legt dabei mehr als 100 Meilen nach Westen zurück, ohne dass dabei eine Höhenänderung festgestellt werden kann. Wenn die Höhe der Sonne zwei Stunden vor oder nach dem Schiffsmittag gemessen wird, dann würde eine Längenberechnung auf Grundlage einer vorliegenden Breite nur einen kleinen Fehler verursachen.

Kapitän Sumner war sich dessen bewusst. Deshalb war es ein großes Glück, dass er die Höhe der Sonne noch zwei Stunden vor dem Schiffsmittag messen konnte. Er machte sich Sorgen um seine Position, weil ihn die starken Winde in Richtung der irischen Lee-Küste getrieben haben konnten. Sein Kurs war zu diesem Zeitpunkt Ost-Nordost und er hatte nur eine ältere Koppelposition.

Aus der gemessenen Höhe und der Koppelbreite konnte er jetzt eine Chronometerlänge und damit eine Position errechnen. Diese lag dann sogar östlich von seiner Koppelposition und somit weiter und sicherer von der irischen Küste entfernt. Als vorsichtiger Seefahrer wusste er allerdings auch, dass die so ermittelte Position einen erheblichen Fehler aufweisen konnte, denn die Breite, die seiner Berechnung zugrunde lag, war nur gekoppelt und somit geschätzt und konnte falsch sein. Also versuchte er herauszufinden, was die Konsequenzen dieses Fehlers wären.

***Bild 1.7: Karte aus dem Buch von Sumner, in dem er die Entdeckung der Standlinie beschrieb.***

Unter Verwendung derselben gemessenen Höhe und einer Breite, die diesmal zehn Meilen weiter nördlich und damit noch näher an der gefährlichen Lee-Küste Irlands lag, rechnete er ein zweites Mal. Dabei fand er jedoch eine Position, die unerwartet noch weiter östlich lag als die vorherige. Eine dritte Berechnung mit einer angenommenen Breite, die um weitere zehn Meilen nördlicher lag, ergab dann eine dritte Länge, die sich ebenfalls noch weiter östlich als die beiden vorherigen befand. Mit diesen Ergebnissen widmete sich Sumner seiner Karte und sah, dass sich alle drei errechneten Positionen auf einer geraden Linie befanden. Diese Linie ist auf der Karte im Bild 1.7 zu sehen.

Da wurde ihm klar, dass diese Linie ein kleines Stück der Kreislinie einer Höhengleiche ist. Höhengleichen bzw. Höhenkreise waren ihm bekannt. Man fand sie auch schon auf uralten Astrolabien. Eine Senkrechte durch die Mitte dieser Linie musste das Azimut zur Sonne sein. Jeder Beobachter auf dieser Linie hätte die Sonne zur selben Zeit in derselben Höhe beobachten können und sein Schiff befand sich irgendwo auf dieser Linie.

Es war einer dieser ungewöhnlichen Zufälle in der Geschichte. Die erhaltene Linie war nicht nur fast mit seiner Kurslinie identisch, sondern lief auch direkt auf den Leuchtturm „Small’s Rocks“ zu. Das ist ein wichtiges Seezeichen vor der Westküste von Wales. Kapitän Sumner entschloss sich dazu, den Kurs entlang der entdeckten Linie beizubehalten, auf der früher oder später der Leuchtturm „Small’s Rocks“ gesichtet werden würde. Einige Zeit später wurde der Leuchtturm trotz des dichten Wetters entdeckt und die Reise konnte dann sicher entlang der Westküste Englands fortgesetzt werden.

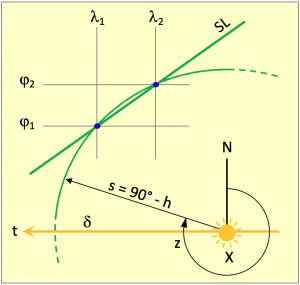
Bild 1.8: Konstruktion einer Sumnerlinie. Deklinationsbreite 𝛿, Sonnenbildpunkt X, Radius s und der Höhenkreis passen natürlich auf keine Seekarte im üblichen Maßstab. Die Darstellung dieser Elemente dient hier nur zur besseren Illustrierung.

Dies war neu. Bild 1.8 zeigt das Geschehen schematisch. Nach nur einer einzigen Beobachtung eines Gestirns werden zwei Breiten 𝜑1 und 𝜑2 gewählt, für die dann die Längen 𝜆1 und 𝜆2 für dieselbe Beobachtung, also mit den gleichen Werten von 𝛿 und h, berechnet werden. Das funktioniert auf die gleiche Weise, wie sie in 1.4 zur Berechnung der Chronometerlänge beschrieben worden ist, und war den Seeleuten längst bekannt. Abweichend davon wird keine Koppelbreite verwendet, sondern zwei Breiten, von denen die eine ein Stück nördlich und die andere ein Stück südlich von der Koppelbreite vermutet werden.

Das lieferte zwei Punkte auf einer Karte und wenn man diese miteinander verband, so hatte man eine Linie, auf der sich das Schiff befinden musste, eine Standlinie, die im Bild mit SL gekennzeichnet ist.

Sumner erkannte, dass seine Standlinie nur ein kurzer Abschnitt der Kreislinie eines Höhenkreises ist und dass er mit seinen Berechnungen eine dicht an der Peripherie liegende Sekante an den Höhenkreis konstruiert hatte.

Diese konnte man auch verlängern und dann auf der Karte sehen, wo sie hinführte. So konnten von einer Standlinie Kurse abgeleitet werden, die parallel und sicher an einer unsichtbaren Küste entlangführten oder sogar direkt auf Land und damit einen Zielhafen ansteuerten. Außerdem konnten an einem Tag zwei Standlinien bestimmt werden, wenn man die Höhe der Sonne einmal vormittags und später am Nachmittag festlegte. Möglich waren auch zwei Vormittags- oder zwei Nachmittagsmessungen. Der eigene Standort muss dann im Sinne einer Kreuzpeilung dort sein, wo sich die Standlinien kreuzten. Sumner verfasste ein Buch, das 1843 unter dem folgenden Titel erschien:

„A NEW METHOD OF FINDING A SHIP’S POSITION AT SEA“

Seine Methode war sehr gut nachvollziehbar und wurde von den Seefahrern sofort angenommen. Mit den auszuführenden Berechnungen waren sie längst vertraut. Somit war jetzt erstmalig eine Möglichkeit gefunden, unabhängig vom Schiffsmittag, zu beliebigen Zeiten auf See ohne Landsicht und mit einfachen Mitteln einen Standort zu finden.

Eine Besonderheit bei der Navigation mit der Sonne besteht darin, dass die zwei Höhen in einem Zeitabstand von mehreren Stunden gemessen werden müssen. Die dabei entstehende Ortsveränderung muss natürlich berücksichtigt werden. In seinem Buch gab Sumner auch darauf eine Antwort. Darin bezeichnete er mit AA’ die erste und mit BB’ die zweite Standlinie. Das Zitat lautet:

„Wenn das Schiff seine Position geändert hat, dann setze die zwischen den Beobachtungen gesegelte Entfernung in Kursrichtung von einem beliebigen Punkt der Linie AA‘ ab. Zeichne durch diesen Zielpunkt eine gerade Linie parallel zur Linie AA‘ bis diese sich mit der Linie BB‘ schneidet. Dieser neue Schnittpunkt mit BB‘ ist die Schiffsposition zum Zeitpunkt der zweiten Beobachtung.“

In den USA widmete man der Sumner’schen Methode eine geradezu offizielle Aufmerksamkeit. Das nautische Institut zu Boston ernannte ein Komitee zur Prüfung der Methode, das zu dem Ergebnis kam, dass sie auf vollkommen richtigen Grundsätzen basiert. Man sah schon damals in diesem Verfahren den Beginn einer neuen Ära in der praktischen Navigation. Dies hatte auch nochmal eine Steigerung der Chronometerproduktion zur Folge. In der US-Marine wurde der Befehl erteilt, jedes Schiff so auszustatten, dass mit der Sumner’schen Methode navigiert werden konnte. Im Jahre 1844 gelangte diese nach England und von dort in die englischen Kolonien im Pazifik und im Orient. Nur in Frankreich wurde die Methode erst einige Jahre später benutzt.

1.7.2 Marcq Saint Hilaire

Die Entdeckung von Sumner verbreitete sich schnell, denn seine Methode wurde gut verstanden. Die Berechnungen waren schon länger Routine, da sie mit der Ermittlung der Chronometerlänge identisch sind. Als nachteilig wurden nur die unvermeidlichen Standortabweichungen empfunden. Diese sind eine Folge der in der Grafik im Bild 1.8 sichtbaren Erhebung des Kreissegments über den linearen Sehnenabschnitt der Standlinie hinaus. Die Ursache dafür ist die große Differenz von einem ganzen Grad zwischen den zu schätzenden Breiten. Sie ist aber nötig, damit die Standlinie, die Verbindungslinie zwischen den Schnittpunkten und darüber hinaus, im richtigen Winkel eingezeichnet werden kann. Je dichter diese Punkte zusammenliegen würden, desto spekulativer wäre es, mit einem Lineal den richtigen Winkel einer Standline durch sie hindurch zu treffen. Deshalb wäre es optimal, wenn die Standlinie als Tangente an den Höhenkreis konstruiert werden könnte. Dies gelang im Jahre 1875 dem französischen Fregattenkapitän Saint Hilaire. Er verfügte über außergewöhnliche Kenntnisse in Mathematik und sphärischer Trigonometrie und veröffentlichte seine Studien in einer maritimen Kolonialzeitschrift.
Zu jener Zeit galt der Sumner Methode ein großes Interesse. So wurde auch darüber diskutiert, auf welche Weise Fehler in der Verwendung der beobachteten Höhe, egal woraus diese resultieren, direkt aus der Winkelmessung oder aus der Beschickung einer Sextantenablesung korrigiert werden können. Darüber veröffentlichte Hilaire im Oktober des Jahres 1873 in einem Artikel eine Notiz. Diese lautet in deutscher Übersetzung:

„Wenn man also nach der Berechnung und dem Konstruieren einer Höhe bemerkt, dass bei dieser Höhe ein gewisser kleiner Fehler [wie Ho – He] begangen wurde, korrigiert man die resultierende Höhe, mit einer Parallelen zu der bereits gezeichneten Linie [Positionslinie] in einer Entfernung in Meilen, die dem erwarteten Fehler in Minuten entspricht, in Richtung des Himmelskörpers [Azimut, Z] oder in die entgegengesetzte Richtung, je nachdem, ob die verwendete Höhe zu klein oder zu groß war.“

Diese Korrekturidee war nicht neu und konnte in den meisten Navigationslehrbüchern der damaligen Zeit im Zusammenhang mit der Erörterung der Sumner Methode gefunden werden. Hilaires Beitrag bestand darin, zu erkennen, dass dieselbe Korrekturidee auch auf die Differenz zwischen der vom Schiffsort aus beobachteten Höhe eines Himmelskörpers und der Höhe von einer angenommenen naheliegenden Position aus angewendet werden kann, um die wahre Standlinie zu bestimmen. Es dauerte dann aber noch knapp zwei Jahre, bis Hilaire seine Methode veröffentlichte. In seiner zweiten Publikation beschreibt Hilaire seine Methode genau. Am Ende seiner Ausführungen fasst er den Kern seiner Überlegungen in wenigen, kurzen Sätzen zusammen. Die deutsche Übersetzung lautet:

„ Zusammengfasst gilt: Zum Berechnen einer Beobachtung berechne die Höhe [He] und das Azimut [Z] des Sterns für die DR-Position [e] und den Beobachtungszeitpunkt. Subtrahiere die berechnete Höhe von der beobachteten Höhe [Ho – He]. Betrachte diese Differenz als einen Versatz des Schiffes. Dabei ist der Kurs durch das Azimut gegeben und die Distanz durch die Höhendifferenz. Korrigiere die Position [e’] entlang dieser Route.“

Zuerst wird also die Sonne beobachtet und die beobachtete Höhe h_b sowie die sekundengenaue Zeit der Beobachtung werden festgestellt und festgehalten. Im Weiteren muss nun die Position eines Gissortes bestimmt werden. Hilaire hat dafür die DR-Position, also den Koppelort als Gissort benutzt. Für diesen Gissort werden jetzt die Höhe zum Beobachtungszeitpunkt und das Azimut berechnet. Dazu sind zwei Formeln nötig, die wohl als die wichtigsten und am häufigsten gebrauchten in der Navigationsgeschichte der vergangenen 150 Jahre gelten. Deshalb werden sie an dieser Stelle auch gezeigt, ohne dass näher darauf eingegangen wird. Die Formeln lauten:

Höhenformel:

$h_c=\sin^{-1}\big(\sin\varphi\,\sin\delta+\cos\varphi\,\cos\delta\,\cos t\big)$

Azimutformel:

$z*=\cos^{-1}\frac{\sin\delta-\sin\varphi\,\sin h_c}{\cos\varphi\,\cos h_c}$

Um die Formeln anwenden zu können, müssen die Deklination 𝛿 und die Variable t bekannt sein. Die Variable t bezeichnet den Ortsstundenwinkel des Gissortes. Ortsstundenwinkel werden oft auch mit LHA (Local Hour Angle) bezeichnet. Unter t bzw. LHA wird nichts weiter verstanden, als die Meridiandistanz eines benannten Ortes bis zum augenblicklichen Bildpunkt der Sonne, und zwar immer nur nach Westen zählend. Somit ist der Greenwichwinkel GHA (dt. Grt) der LHA des Ortes Greenwich.

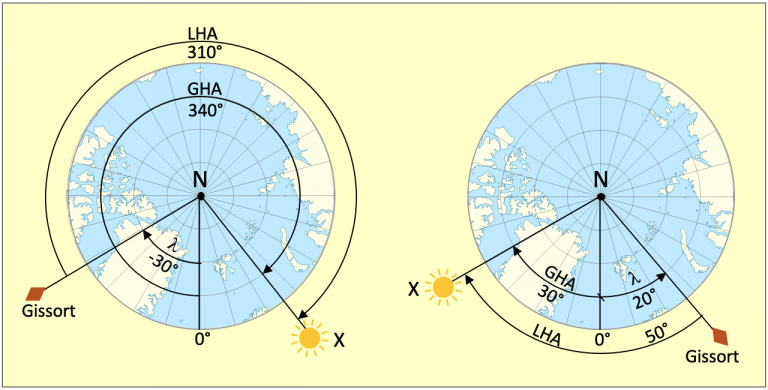
Bild 1.9: Der LHA eines Ortes, oft auch als t bezeichnet, ist die Summe von GHA und dem Längengrad des zu betrachtenden Ortes. Westgrade besitzen ein negatives Vorzeichen. Der LHA wird nur westwärts gezählt.

Wie Bild 1.9 zeigt, errechnet sich der LHA als Summe von Greenwichwinkel GHA und dem geografischen Längengrad eines zu betrachtenden Ortes, also t = 𝜆 + GHA. (Westgrade sind negativ)
Beide Werte, die Deklination 𝛿 und der Greenwichwinkel GHA müssen einem nautischen Jahrbuch entnommen werden, und zwar für die Sekunde, die sich der Navigator notiert hatte, in welcher er die Sonne im Fernrohr des Sextanten auf die Kimm setzte. Da jetzt alle Werte bekannt sind, kann mit der ersten Formel die Höhe h_c berechnet werden. Das Ergebnis gibt an, wie hoch die Sonne in der Sekunde der Beobachtung am Gissort gestanden hatte. Der Index c besagt dabei, dass es eine berechnete (c = calculated) Höhe ist. Die Messung auf dem Schiff lieferte für dieselbe Sekunde die beobachtete Höhe hb. Aus den beiden Höhen wird nun ihre Differenz 𝛥h = h_b – h_c berechnet. Diese Höhendifferenz wird im englischen Sprachgebrauch als Intercept bezeichnet und auch die Methode ist als Intercept Methode bekannt geworden.

Da nun alles Erforderliche vorliegt, kann mit der Konstruktion der Standlinie, entweder direkt auf der Seekarte oder auf vorbereiteten Leerkarten erfolgen. In Leerkarten sind die Meridianabstände den Abständen der Breitenkreise so angepasst, dass Winkel mit einem normalen Winkelmesser ohne Umrechnung direkt eingezeichnet werden können. Die Konstruktion einer Standlinie verdeutlicht Bild 1.10.

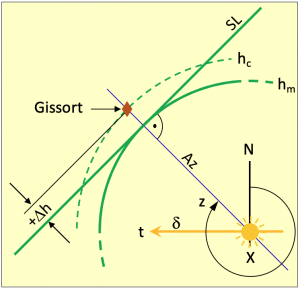
***Bild 1.9: Konstruktion einer Standlinie nach Saint Hilaire.***

Begonnen wird die Konstruktion z. B. mit einem kleinen Kreuz, das die Position des Gissortes markiert. Durch diese Markierung wird jetzt eine Linie im Winkel des ausgerechneten Azimuts gezogen. Das ist der Azimutstrahl Az. Als Nächstes wird die Differenz 𝛥h, die in Bogenminuten vorliegt als Distanz in Seemeilen vom Gissort ausgehend auf dem Azimutstrahl abgetragen.
Das Vorzeichen dieser Differenz ist jetzt sehr wichtig. Ist es positiv, dann erfolgt die Abtragung, wie im Bild gezeigt, in Richtung Sonne. Das Schiff war dann während der Beobachtung näher an der Sonne, als der Gissort. Man musste den Blick höher richten. Ist die Differenz negativ, dann wird das Intercept vom Gissort und von der Sonne weg auf dem Azimutstrahl abgetragen. An der Stelle, an der eine Abtragung endet, wird die Standlinie senkrecht zum Azimutstrahl eingezeichnet. Das Bild ist eine sehr verzerrte Darstellung, in der sogar der Bildpunkt der tausende Meilen entfernten Sonne eingezeichnet ist. Der Gissort als neuer Bezugspunkt ermöglicht Konstruktionen in seinem Nahfeld, ein Vorteil für zeichnerische Lösungen. Der Kreuzungspunkt mit einer zweiten, einige Stunden später beobachteten Standlinie liefert den Standort.

1.7.3 Resümee

Saint Hilaire erfand kein rundum neues Navigationsverfahren. Das überragende und bleibende historische Verdienst bestand vielmehr darin, die Konstruktionsweise der von Thomas Sumner erfundenen Standlinien so modifiziert zu haben, dass die grafische Standlinien-Navigation sehr viel zielsicherer und genauer ausgeführt werden konnte. Das war zu jener Zeit sehr wichtig, denn es gab ja keine Computer. Die Sumner Methode hatte schon gezeigt, dass die Zukunft in der grafischen Navigation zu sehen ist.

Das markante Kennzeichen des Hilaire Verfahrens ist der Gissort. Dieser bewirkt eine Maßstabsverkleinerung in den Grafiken, die erst dadurch wesentlich übersichtlicher und präziser werden. Als Preis dafür musste Hilaire auch Nachteile in Kauf nehmen. So ist die Festlegung eines Gissortes an sich schon mal lästig und hat auch zur Folge, dass mit dem Verfahren gar nicht der Standort gefunden werden kann, sondern ein Ort, der wesentlich näher am wahren Standort liegt, als der Gissort. Auch Höhen über 80° sollten nicht gemessen und verwendet werden.

Wenn es darum geht, eine Standlinienmethode als Computer-App zu programmieren, dann sollte von der Hilaire Methode Abstand genommen werden. Saint Hilaire hat die Sumner Methode nur zeichnerisch verwendungsfähig gemacht. Würden dieselben Dinge, die zu einer zeichnerischen Verbesserung geführt haben in einer Digitalisierung der Methode benutzt, würden sie zu Nachteilen werden. Eine Computer-App nach Sumner hätte dagegen keinerlei Restriktionen. Mit Iterationsroutinen können die Schätzbreiten so dicht zusammengelegt werden, dass die Standlinie quasi zur Tangente wird. Ein Schätzort wäre ebenfalls überflüssig. Es genügte einfach nur die Angabe, ob auf der Nordhalbkugel oder auf der Südhalbkugel der Erde gesegelt wird.

1.7.4 Die Tafelmethode

In der Hilaire-Methode werden für jede Beobachtung nur zwei trigonometrische Formeln zur Berechnung von Höhe und Azimut des Gissortes gebraucht und sonst nur Additionen und Subtraktionen.

So entstand die Idee, Azimut und Höhe für möglichst viele Orte auf der Erde im voraus auszurechnen und in Tafeln zur Verfügung zu stellen. Als Orte wurden die ganzgradigen Kreuzungen von Längengraden mit Breitengraden benutzt. Nicht zuletzt durch die aufkommende Fliegerei entstand die Notwendigkeit, den Rechenaufwand mit den umständlichen Logarithmen zu vermeiden um die Rechenzeit zu reduzieren.

Die ersten Tafelwerke gab es schon 1902. Anfangs wurde nur das Azimut tabelliert. Die Höhe wurde erst in späteren Ausgaben berücksichtigt. Bekannt sind vor allem die „SIGHT REDUCTION TABLES“ des amerikanischen U.S. Hydrographic Office. Deren erste Tafel erschien 1919 unter der Bezeichnung H.O. 201. Besonders die Luftfahrt brauchte diese Tafeln zur schnellen Ortsbestimmung mit einem Sextanten und einem künstlichen Horizont.

Fast schon legendär sind die HO 249 Tafeln geworden, die später von der Nachfolgeorganisation des U.S. Hydrographic Office, dem „Naval Oceanographic Office“ als PUB. NO. 249 herausgegeben wurden. Einige der heute noch aktuellen Tafeln sind bereits im Zweiten Weltkrieg entwickelt worden, speziell zur Verwendung in den US-Air Forces, damit die Bomber ihren Weg sicher über die Ozeane finden konnten. Bis heute nutzen auch einige Fahrtensegler diese Tafeln als Hobby-Navigationssystem oder als Back-up für einen möglichen Notfall, falls die vollelektronische Navigation ausfällt.

***Bild 1.11: Die Cover der drei Bände der PUB. NO. 249***

Die PUB. NO. 249 besteht aus drei Bänden. wobei der erste Band die Fixsterne erfasst und alle fünf Jahre neu aufgelegt werden muss, weil die Fixsterne eben doch nicht so fix sind. Band 2 und 3 erfassen die Breiten von 0° bis 40° sowie 39° bis 89° und sie gelten immer.
Daneben existiert die PUB. NO. 229, die für die Seefahrt erarbeitet wurde. Diese Tafel steht in sechs Bänden in Größe jeweils eines Telefonbuches zur Verfügung. Die Auflösung ist bei diesen Tafeln größer, was mehr Papier erforderlich gemacht hat. Da auch immer noch ein „Nautical Almanac“ hinzukam, war dies eher etwas für die Großschifffahrt als für die Verwendung auf den engeren Segelyachten.

Bemerkenswert ist, dass der Vertrieb der Tafeln lange Zeit ausgesetzt war. Fahrtensegler und Interessenten konnten sich diese nur noch aus dem Internet als PDF herunterladen. Der Band 1, der nach fünf Jahren sowieso ungültig wird, weil Fixsterne nicht fix sind, war schon lange nur noch Makulatur. Doch inzwischen werden alle Bände wieder gedruckt und als Bücher verlegt. Auch der Inhalt von Band 1 ist neu erstellt und erscheint nun wieder alle fünf Jahre. Es scheint fast so, als hätten die Herausgeber die Bedeutung der Astronavigation wiederentdeckt.

1.8 Künstliche Himmelskörper

Als die Satellitennavigation 1996 offiziell ihren Betrieb aufnahm, kam dies einer Revolution gleich. Positionen konnten sehr schnell, mit größter Leichtigkeit und exakt gefunden werden. Schon bald verfügte sogar jedes Auto über ein Straßennavigationssystem. Container erhielten GPS-Tracker, damit ihr Standort weltweit verfolgt werden konnte, und selbst Spielzeuge wie kleine Drohnen wurden mit GPS-Ortungssystemen ausgestattet, damit sie ihren Weg zurück zum Startplatz finden konnten.

Der Betreiber des ersten Satellitennavigationssystems GPS (Global Position System) war das amerikanische Militär. Es nutzte nicht nur Schiffen und Flugzeugen bei der Navigation, auch Raketen und Marschflugkörper konnten damit präzise auf ein Ziel gelenkt werden. Die zivile Nutzung ist bei alledem nur ein Nebeneffekt.

Aufgrund des militärischen Gebrauchs durch die Amerikaner musste Russland sein eigenes System GLONASS errichten und die Europäer folgten mit GALILEO. Aber auch China hat sei 2022 sein eigenes System GROSSER BÄR. Zurzeit existieren also vier unabhängige Systeme, die auch die zivile Nutzung sicherer machen sollen. Inzwischen blickt man auf drei Jahrzehnte eines überwiegend störungsfreien, friedlichen Betriebes zurück. Doch wie sicher sind diese von Menschen geschaffenen Systeme wirklich, wenn ihre Präzision und Funktion von den Betreibern jederzeit beeinflusst werden können und in einem Konfliktfall auch den Angriffen eines Feindes ausgesetzt sein könnten?

Ende der Neunzigerjahre setzte die Marineakademie in den USA den Unterricht in astronomischer Navigation aus. Man sah zu diesem Zeitpunkt keine Gefahren. Doch ein Jahrzehnt später wurden Betriebseigenschaften und Schwachstellen des Systems entdeckt, die es unter bestimmten Bedingungen unzuverlässig oder sogar unbrauchbar machen könnten. So hat ein Satellit nur eine bestimmte Lebensdauer, nach der seine Signalstärke abnimmt. Die Gefahr, dass alternde Satelliten aus Kostengründen nicht schnell genug ersetzt werden könnten, wurde sehr real. Die schwachen Funksignale der Satelliten könnten auch durch Feindeinwirkungen, Cyberangriffe oder einen Sonnensturm gestört, beeinflusst oder sogar unbrauchbar werden. Sonnenstürme können sich auf die Steuerung eines Satelliten auswirken und ihn dadurch sogar zum Absturz bringen. Eine neue Gefahr stellt auch die anwachsende Menge an Weltraumschrott dar, der durchaus das Potenzial besitzt, Navigationssatelliten zerstören zu können.

Aufgrund dieser Überlegungen machte sich die Sorge breit, dass durch die wachsende Abhängigkeit von der vollelektronischen Navigation die Kompetenz in der astronomischen Navigation gänzlich verloren geht. Die Konsequenz bestand darin, dass im Jahr 2015 wieder die Ausbildung in astronomischer Navigation an der Marineakademie in den USA eingeführt wurde. Dahingegen hat die US-Handelsmarine die klassische Navigation mit dem Sextanten als Notfallsystem auf ihren Schiffen nie aufgegeben.

Obwohl all diese Gefahren immer wieder zitiert werden, wird Astronavigation als Notfalloption gerne verdrängt oder nicht ernst genommen. Irgendwie ist es auch schwer vorstellbar, dass Flugzeugträger heutzutage mit einem Sextanten navigieren müssten, so wie im Zweiten Weltkrieg. Doch auf einer Yacht kann schon ein simpler Stromausfall die Satellitennavigation außer Gefecht setzen und ohne Papierseekarten an Bord ist auch ein Standort, den ein Smartphone angibt, ziemlich nutzlos.

1.9 Astronavigation heute

Die allermeisten Segler geht das Thema Astronavigation nichts an. Sie wollen überhaupt nicht auf den Gedanken kommen, dass Satellitennavigation auch mal nicht verfügbar sein könnte. Außerdem gilt die Meinung, dass eine erst mühevoll erlernte Methode zur astronomischen Navigation im Notfall sowieso nichts nützt, weil die dazu erforderlichen Kenntnisse und Voraussetzungen in dem Moment, wo sie wirklich gebraucht werden, vergessen sind. Diese Einstellung gründet sich auf einem Wissen über das grafische Höhendifferenzverfahren von Saint Hilaire in der Art, wie es heute verwendet werden soll und ist durchaus nachvollziehbar.

Manchmal sind es aber auch die Kosten. Ein Sextant ist nicht gerade ein Schnäppchen und wird je nach Ausführung zwischen 300 Euro und mehr als 1000 Euro zu Buche schlagen. Übungssextanten aus Plastik kosten dagegen nur rund 60 Euro. Doch auch die wären in einem Notfall besser als nichts. Zusammen mit einer kostenlosen App, wie sie hier im Kapitel 2 beschrieben wird, wäre das sogar der Mindestaufwand für ein sicheres Ankommen.

Man soll sich nichts vormachen. Jedes technische System kann ausfallen, so auch die vollelektronische Satellitennavigation. Verbände und Behörden auf der ganzen Welt schufen deshalb Gesetze oder geben Empfehlungen, auf welche Weise Redundanz erzeugt werden kann. So müssen große Schiffe über zwei vollkommen unabhängige Satellitennavigationssysteme verfügen. Auf kleineren Schiffen, darunter fallen auch alle Segelyachten, ist das nicht umzusetzen. Dort gilt die Empfehlung, dass nautische Unterlagen und ein Sextant an Bord mitzuführen sind. Damit soll dann in einem Notfall navigiert werden – natürlich mit der komplexen Höhendifferenzmethode von Saint Hilaire. Doch ohne Routine wird das niemand können.

Astronomisch zu navigieren, kann auf verschiedenen Wegen gelernt werden. Spezialisierte Segelschulen bieten dazu Lehrgänge an, die jedoch kostenpflichtig sind und je nach gebotenem Umfang und Stoffauswahl zwischen einem und mehreren Tagen dauern können. Wenn das Gelernte dann aber nicht gleich angewendet und ständig trainiert wird, damit Routine entsteht, dann war so ein Lehrgangsbesuch lediglich eine Investition in die Erweiterung des Allgemeinwissens. Wer das Selbststudium bevorzugt, findet zum Thema genügend Fachliteratur. Aber auch im Internet finden sich zahlreiche Beiträge und Beispiele dafür, wie astronomisch navigiert werden kann. Doch nahezu alles, was in Segelschulen gelehrt, in der nautischen Literatur geschrieben steht oder im Internet zu finden ist, dreht sich um das Höhendifferenzverfahren von Saint Hilaire. Es scheint fast so, als sei dieses Verfahren ein Synonym für astronomische Navigation.

In der Tat ist das Höhendifferenzverfahren für Segler, die grafisch mit Bleistift, Lineal und Zirkel auf Papier navigieren wollen, die beste Methode. Das ist aber nur eine ganz kleine Gruppe. Die größere Mehrheit derjenigen, die Astronavigation als Backup an Bord haben wollen oder aus anderen Gründen mit einem Sextanten navigieren möchten, ohne sich irgendwelchen Lernstress antun zu wollen, benötigt eine Navigations-App. Diese sollte auf einem Computer oder einem Mobilgerät lauffähig sein und ihre Benutzung sollte neben der Handhabung eines Sextanten keinerlei Voraussetzungen in Mathematik, Astronomie oder astronomischer Navigation voraussetzen. Eine derartige App sollte zudem auch mit einer elektronischen Karte kombiniert sein, wie das in der Satellitennavigation auf einem Kartenplotter geschieht. Eine Beschränkung auf die Sonne als einziges Navigationsgestirn ist in diesem Zusammenhang kein Nachteil. Viele Handelskapitäne in früherer Zeit haben ihr Leben lang erfolgreich nur mit der Sonne navigiert. Außerdem ist eine Beobachtung der Sonne mit einem Sextanten recht schnell zu erlernen. Dagegen erfordert die Nutzung von Sternen als Navigationsgestirne eine Menge Erfahrung und viel Übung.

In existierenden Computer-Apps zur astronomischen Navigation findet, wie sollte es anders sein, immer nur das Höhendifferenzverfahren von Saint Hilaire Anwendung. Man sollte aber wissen, dass Hilaire kein grundlegend neues Navigationsverfahren geschaffen hat. Damals verbreitete sich gerade sehr schnell die neue Standliniennavigation von Thomas Sumner. Diese war im grafischen Gebrauch nicht sehr präzise, doch ohne Computer gab es damals keine andere Möglichkeit. Die Leistung von Hilaire bestand in einer anderen Konstruktionsweise von Standlinien, mit der er die grafische Arbeitstechnik erheblich verbesserte. Seine Arbeit markiert gleichzeitig den Beginn der Ära der sogenannten modernen Navigation. Die endete bekanntlich erst am Ende des 20. Jahrhunderts mit der Inbetriebnahme des ersten Systems einer vollelektronischen Satellitennavigation, dem GPS.

Das Kennzeichen der Standlinienkonstruktion von Hilaire ist die Einführung eines Gissortes. Ein Anwender muss seine aktuelle Position zunächst schätzen. Daraus folgt logischerweise, dass der wahre Standort gar nicht direkt ermittelt werden kann. Das Ergebnis ist eine Position, die dem wahren Standort sehr viel näher liegt, als der Gissort. So ist das Höhendifferenzverfahren mathematisch gesehen eine Näherungsmethode. Die Notwendigkeit des Gissortes ist jedoch nervig und auch die Ursache dafür, dass Gestirnshöhen über 80° nicht mehr verwendet werden sollen, weil dann die Krümmung der Höhengleiche so stark wird, dass mit erheblichen Ungenauigkeiten gerechnet werden muss.

Seltsam ist, dass Entwickler von Navigations-Apps immer nur die von Saint Hilaire – speziell für grafische Arbeitstechniken – optimierte Standlinienkonstruktion in ihren Programmen umsetzen. Dagegen wäre es doch angebracht, am Ursprungsverfahren von Sumner anzusetzen, wie Hilaire es auch getan hat und dann eine spezielle Optimierung für Computeranwendungen zu finden. Das Ergebnis wäre in diesem Fall ein Navigationsprogramm, das mit Standlinien arbeitet, aber keinerlei Restriktionen mehr besitzt. Neben exakten Ergebnissen wären weder ein Gissort anzugeben noch wären Breitenschätzungen nötig. Es müsste lediglich noch angegeben werden, ob auf der Nordhalbkugel oder auf der Südhalbkugel der Erde gesegelt wird.

SY-Zephir

Reisen auf 18 Metern

1 Kleiner Exkurs in die Geschichte der Astronavigation