Präzision und Vergleich der Methoden

Obwohl eine hohe Rechengenauigkeit einer Methode meist wenig mit der erzielbaren Standortgenauigkeit zu tun hat, dürfte es interessant sein zu erfahren, mit welchen Rechengenauigkeiten man bei den verschiedenen Verfahren und Methoden rechnen muss. Ein Standort ist das Ergebnis der Auswertung von zwei Gestirnsbeobachtungen, wobei eine Beobachtung aus der Höhe des Gestirns zu einer bestimmten Zeit besteht. Die Methode und die Beobachtung unterliegen Fehlern, wobei im Folgenden nur zufällige Fehler verstanden werden. Ein Ablesefehler wäre in diesem Sinnne nicht zufällig.

Ein Gesamtfehler, der aus mehreren zufälligen Einzelfehlern hervorgeht ist nicht die arithmetische Summe der Einzelfehler, sondern die geometrische Summe und es gilt das Fehlerfortpflanzungsgesetz:

   

Im Folgenden wollen wir nur zwei Fehlerarten unterscheiden, den maximal möglichen Fehler des verwendeten Rechenalgorithmus und den Beobachtungsfehler. Beide Arten sind zufällig und setzen sich ebenfalls aus einer Summe von verschiedenen Fehlern zusammen. Dazu ein einleitendes Beispiel. Ein Navigator hat einen Standort mit einer Abweichung von 2,06 Seemeilen gegenüber GPS gefunden. Die von ihm angewendete Rechenmethode läßt einen Fehler von 0,5 Seemeilen zu und wir fragen uns jetzt, wie groß dabei wohl der Beobachtungsfehler gewesen sein mag. Es ist kaum zu glauben, das Fehlerfortpflanzungsgesetz liefert mit

   

einen Wert von 2 nm, der den Umständen der Beobachtung zugerechnet werden kann. Das sind Fehler aus der Höhenmessung, wie Instrumentenfehler, Einfluss von Seegang, Wind usw. auf eine sichere Höhenbestimmung, Einfluss der Refraktion und Fehler in der Zeitmessung. Für die Rechenmethode bleiben dann nur 0,06 nm Abweichung stehen. Daraus kann geschlussfolgert werden, dass ein Fehler in der angewendeten Methode belanglos ist, wenn er 0,5 Seemeilen nicht übersteigt. Er wird in der Praxis einfach keine Rolle spielen.

 

Das Höhendifferenzverfahren

Diese Methode, die 1875 erstmalig von dem Fregattekapitän Saint Hilaire vorgestellt wurde, ist die wohl am meisten benutzte astronomische Navigationsmethode überhaupt und war mehr als 100 Jahre die Standardmethode in der weltweiten Seefahrt. Für viele ist sie sogar das Synonym für Astronavigation überhaupt. Mit ihr kann auf grafischem Wege ein Standort gefunden werden. Notwendig sind dazu die Daten zweier Beobachtungen, bestehend aus der Beobachtungszeit und der Gestirnshöhe und einem geschätzten Standort. Mit dem Verfahren wird kein Standort berechnet, sondern es wird ein Ort ermittelt, der dem Standort sehr viel näher liegt, als der geschätzte Ort. Damit ist der Fehler dieser Methode davon abhängig, wie genau der Schätzort bestimmt werden kann und diese Schätzung ist gegenüber dem wahren Standort immer zufällig. Das Verfahren arbeitet iterativ. Auf eine Schätzung wird eine Methode angewendet, die nur die Schätzung verbessert.

Der Verfahrensweg der Hilaire Methode ist bereits eine Iteration (math.: Wiederholung), wenngleich die ursprüngliche Schätzung nach anderen Methoden erfolgte, z. B. als Kopplung. Ein verbesserter Schätzwert kann jedoch mit derselben Methode weiter verbessert werden. Eine dritte und vierte Iteration bewirken schließlich, dass das rechnerische Ergebnis dem wahren Standort schon bis auf wenige Meter heranrückt, selbst dann, wenn der ursprüngliche Schätzwert einige Grade neben dem wahren Standort gelegen hätte.
Iterationen sind jedoch nur machbar, wenn das grafische Verfahren zuvor digitalisiert wird. Da alle Verfahren zur astronomischen Navigation digitalisierbar sind, hat dieses Verfahren den Nachteil, dass auch dann immer noch eine Standortschätzung nötig ist. alle anderen Verfahren besitzen diesen Nachteil nicht und sind darüber hinaus sehr viel einfacher zu digitalisieren.
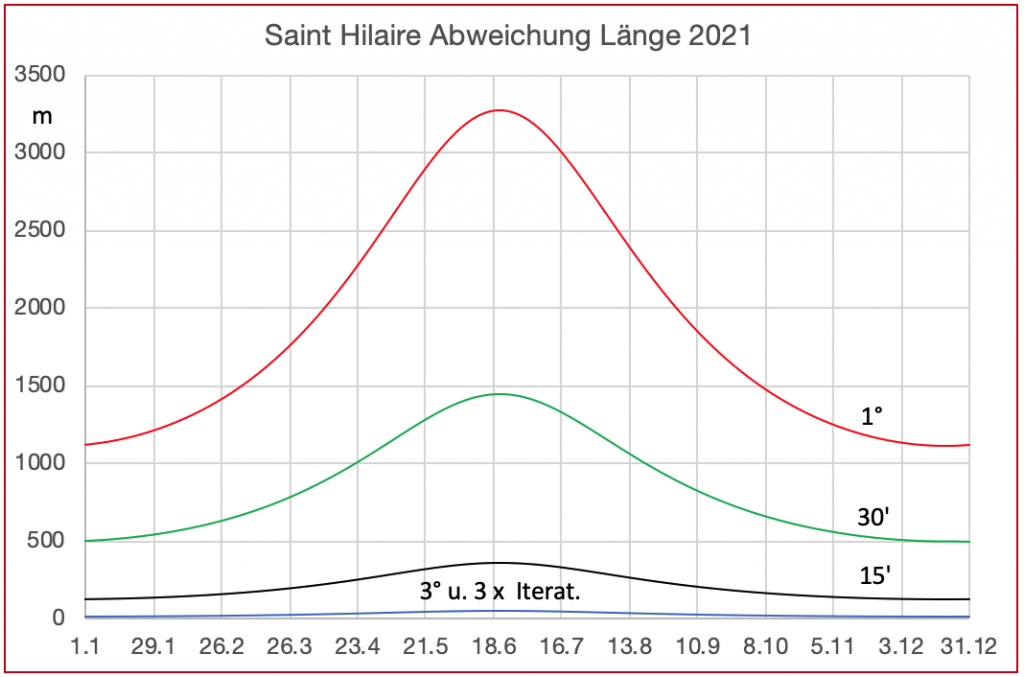
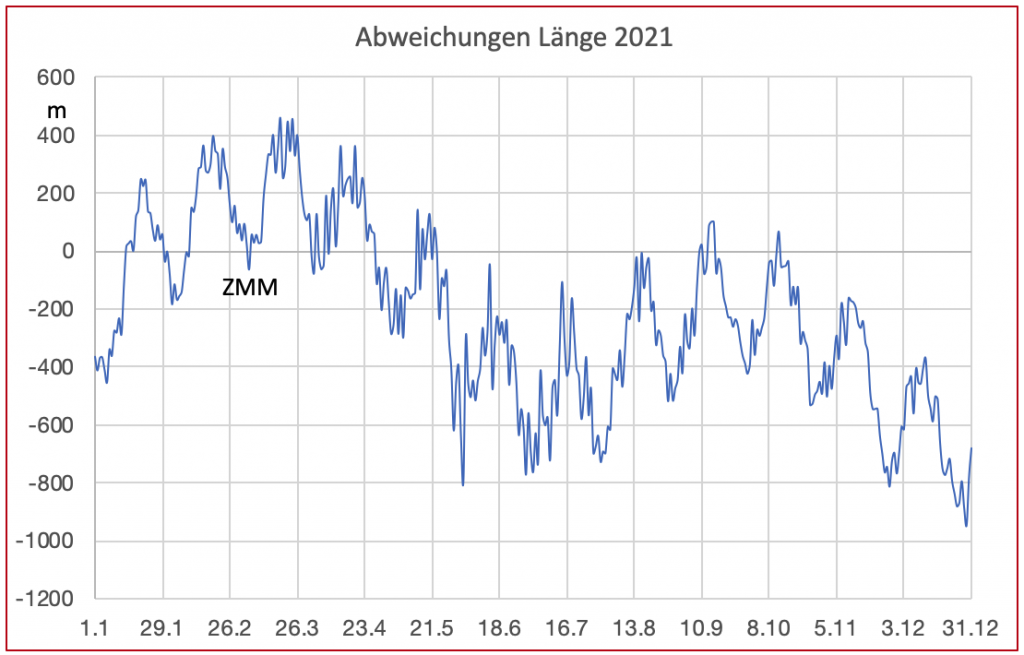
Für das Jahr 2021 sind die zu erwartenden rechnerischen Abweichungen der Länge in Metern vom tatsächlichen Standort in einem Diagramm im Bild 1 erfasst. Die verschiedenen Kurven gelten für unterschiedliche Abstände des Schätzortes in 45° rechtweisend Nord vom wahren Standort. Bei der roten Kurve liegt der Schätzort 1° nördlicher und 1° östlicher als der wahre Standort. Die Abweichungen wären negativ, wenn der Schätzort in derselben Entfernung südwestlich liegen würde.

Zu erkennen ist ein Anstieg der Abweichungen im Sommer. Der Grund dafür ist die größere Höhe der Sonne und damit der kleinere Durchmesser der Höhengleichen. Hier wirkt sich aus, dass mit geradlinigen Standlinien Abschnitte eines Kreisbogens immer schwieriger approximiert werden können. Das Bild gilt gleichermaßen auch für beide Hemisphären Süd- und Nordhalbkugel.

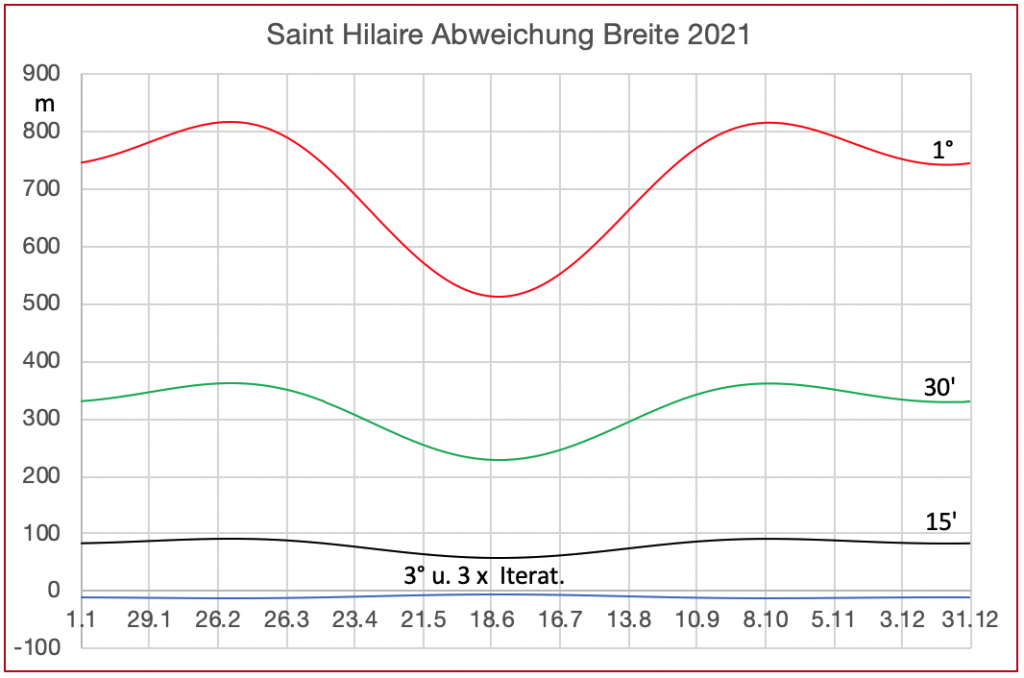
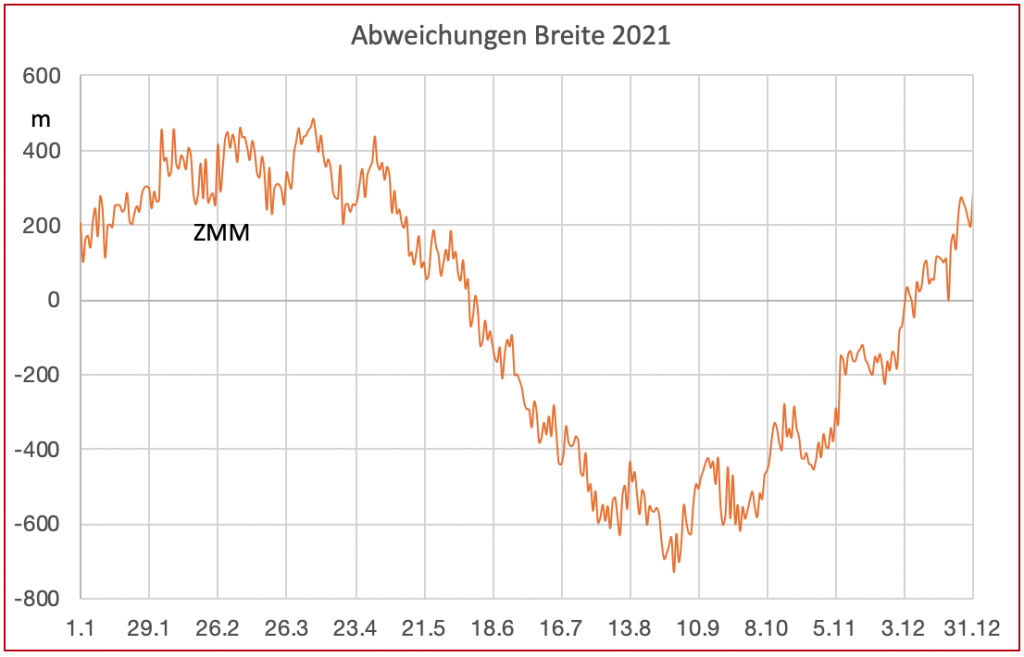
Bild 2 zeigt die maximal zu erwartenden rechnerischen Abweichungen in der Breite und in Abhängigkeit vom Datum. Auch dieses Diagramm gilt für beide Halbkugeln. Im Gegensatz zu Längenabweichungen, die je nach Lage des Schätzortes zum Standort positiv und negativ sein können, sind Abweichungs-Beträge in der Breite immer ohne Vorzeichen zu betrachten. So gilt unabhängig von der Lage des Schätzortes vom wahren Standort: Auf der Nordhalbkugel ist die ausgerechnete Breite immer nördlicher- und auf der Südhalbkugel ist die ausgerechnete Breite immer südlicher als die wahre Breite.  Außer natürlich, wenn Schätzort und Standort identisch sind. Die Erklärung liegt wieder in den geradlinigen Standlinien. Diese tangieren die Höhengleichen nur und liegen sonst immer nur außerhalb der Höhengleichen. Sie können sich deshalb auch nur außerhalb der Höhengleichen kreuzen und dieser Kreuzungspunkt liegt näher zum jeweiligen Pol als der wahre Standort. Der wahre Standort ist die tatsächliche Kreuzung der Höhengleichen.

 

Die Idee von Jean-Borda

Der Chevalier Jean de Borda ist heute völlig unbekannt und seine Idee zur Bestimmung der Breite aus zwei Höhen kennt auch niemand mehr. Wer jedoch seine Standortbreite kennt und die sekundengenaue Zeit, in der man eine Gestirnshöhe gemessen hat, der hat dann kein Problem mehr, seine Standortlänge zu berechnen.

Die Ideee von Borda ist die wohl einfachste überhaupt. Wenn man den Stundenwinkel kennt, den die Sonne in der Zeit zwischen zwei Beobachtungen überstreicht, dann müsste dieser Winkel durch 15 geteilt, die zwischen den Beobachtungen verstrichene Zeit ergeben. So einfach das auch ist, im Jahr 1772 konnte für eine Umsetzung dieser Idee keine analytische Berechnungsmöglichkeit gefunden werden. Heute wäre das kein Problem, doch dieser Gedanke ist längst nicht mehr präsent. Die Methode von Borda arbeitet übrigens mit nur einer einzigen trigonometrischen Formel. Nach Bestimmung der Breite auf numerischem Wege findet man dann auch die Standortlänge mittels einer einfachen Addition. Eine vorherige Standortschätzung ist dabei unnötig. Allerdings geht das nur mit einem Computerprogramm. Ein Taschenrechner ist nicht ausreichend. Mit EXCEL oder Numbers auf dem heimischen Computer funktioniert das aber ganz gut und man kann das Programm dann auch auf einem Smartphon nutzen.

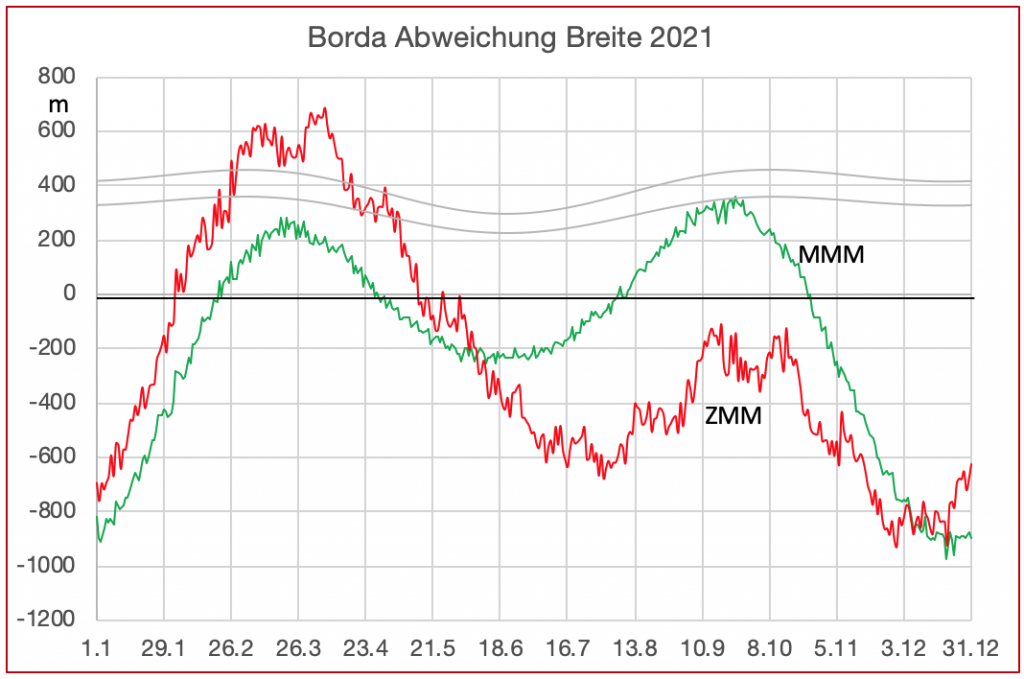
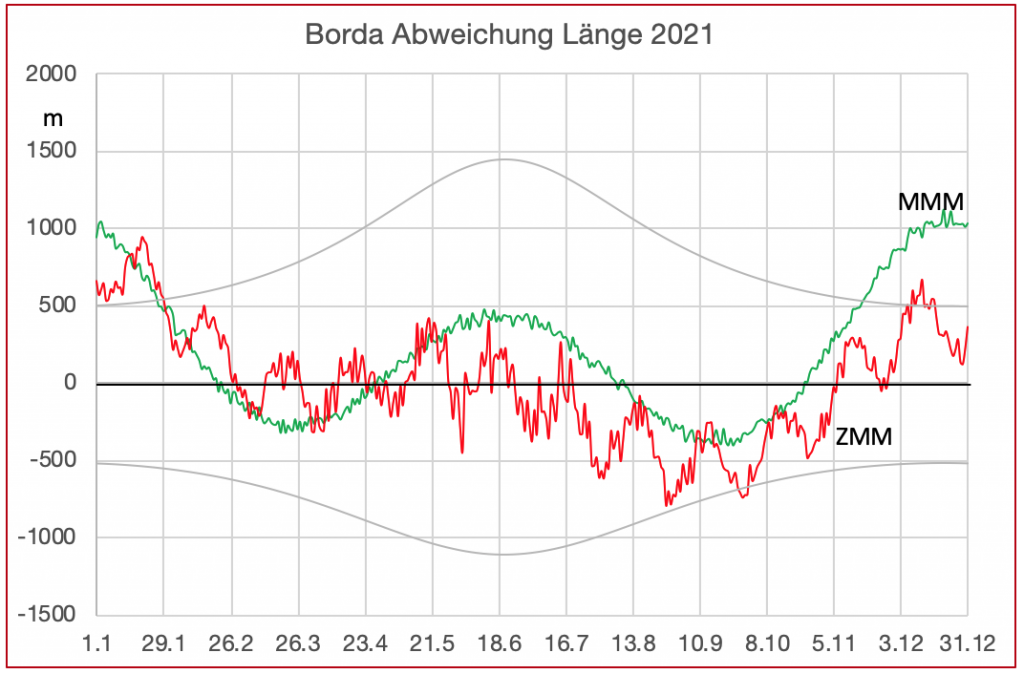
Bild 3 zeigt zwei Längenabweichungen, berechnet von zwei identischen Programmkopien. Die eine Kopie arbeitet mit genauen Ephemeriden, so wie sie das Nautische Jahrbuch in der Vergangenheit bereitgestellt hat und die zweite Kopie mit den hier selbst berechneten Ephemeriden. Die grauen Kurven sind die Fehlergrenzen der Zweihöhenmethode, wenn der Gissort ein halbes Grad bzw. im Umkreis von 30 Seemeilen entfernt liegt. Erkennbar ist, dass in den Sommermonaten, wenn die Sonne höher steht, die Abweichungen an kleinsten sind, also genau umgekehrt wie bei der Zweihöhenmethode.
Bild 4 zeigt, dass die Abweichungen in der Breite ein etwa gespiegeltes Verhalten in den Beträgen aufweisen. Die beiden grauen Linien geben die Beträge der Breitenabweichungen bei der Zweihöhenmethode an, die dann entstehen, wenn der Gissort einmal 30′ nördlich und 30′ südlich vom wahren Standort liegt. Wie oben beschrieben, sind bis zu diesen Beträgen die nach Hilaire berechneten Breiten zu den jeweiligen Polen hin vermehrt.
Die Abweichungen liegen sowohl in der Länge als auch in der Breite im Bereich maximal etwa 0,5′ und haben damit keine praktische Relevanz.

 

Das Zweimassenmodell im  Gauß Algorithmus

Der Algorithmus von Carl Friedrich Gauß ist ist das präziseste Verfahren zur astronomischen Standortbestimmung überhaupt. Ein Rechenfehler ist nur noch davon abhängig, ob der Rechner mit 6 Stellen oder mit mit 30 Stellen nach dem Komma rechnet. Es gibt keine Fehlerabhängigkeit vom Radius der Höhengleichen, dafür aber von ihrem Schnittwinkel.

Es soll jetzt untersucht werden, welche Auswirkungen es hätte, wenn anstelle der nur mit hohem Aufwand zu berechnenden Sonnenephemeriden diejenigen verwendet werden, die sich in einfacher Berechnungsweise aus dem Keplerschen Zweimassenmodell errechnen lassen. Zu diesem Zweck wurden zwei identische Kopien eines Navigationsprogramms mit denselben Daten in Höhe und Zeit versorgt. Das eine Programm arbeitet mit Ephemeriden, bei denen die Störungen von Mond und Planeten herausgerechnet sind, dem also ein Mehrmassenmodell zugrunde liegt und das andere Programm arbeitet mit dem einfachen Keplerschen Zweimassenmodell. Dabei erfolgt täglich eine Berechnung, der eine Sonnenhöhe von 50° und ein Stundenwinkel von 52,5°, also eine Zeit von 3,5 h zwischen den Höhenmessungen zugrunde liegt.

Das Diagramm im Bild 5 zeigt die dabei festgestellten Abweichungen in der Länge in Abhängigkeit vom Datum. Die Abweichungen betragen nicht einmal eine halbe Meile und würden deshalb im praktischen Einsatz keinen Unterschied machen.

 

Interessant ist dabei die Welligkeit, die genau betrachtet, mit den Mondphasen zusammenfällt. Es sind genau 12 Mondperioden und die größten Abweichungen treten immer dann auf, wenn Vollmond (Spitze) oder Neumond (Tal) herrscht.

Der bogenförmige Verlauf und die Zackigkeit der Kurven rühren aus dem Vergleich der verschiedenen Ephemeridenquellen und der Mathematik. Hier werden immerhin Strecken von tausenden Seemeilen so miteinander verglichen, dass dabei der einzelne Meter Unterschied herauskommen soll.
Doch auch in der Breite sind, wie Bild 6 zeigt, die Standortabweichungen so gering, dass in der Praxis mit den Daten aus dem Zweimassenmodell gegenüber dem Mehrmassenmodell kein Unterschied festgestellt werden kann.

 

Backup

Ist die astronomische Standortbestimmung überhaupt noch zeitgemäß? Klare Antwort – nein, doch ein professioneller Seefahrer geht niemals ohne ein Backup in der Navigation auf große Reise; das Meer ist kein sicherer Ort. Ein Ausfall der elektronischen Navigation würde sein Schiff ins 19. Jahrhundert zurückschicken. Die Amerikaner haben schon vor einigen Jahren erkannt, dass ein Satellitennavigationssystem unzuverlässig sein könnte. Seitdem lehrt die Marineakademie wieder astronomische Navigation. Im Jahre 2017 machte der erste Jahrgang der Offiziere darin seinen Abschluss.

Umfangreiche Kenntnisse und Fertigkeiten in Astronomie und Mathematik waren in früheren Jahrhunderten Voraussetzungen für das sichere Navigieren an Bord eines Schiffes. Heute muss man das als Unfug ansehen, wenn in einem Notfall die alten Verfahren und dann auch noch mit den alten Mitteln angewendet werden sollen. Sowas kann man vielleicht noch als Hobby machen. Im Zeitalter der Satellitennavigation muss im Notfall jeder auf Astronavigation wechseln können, ohne dass dafür die Kenntnisse eines Navigators aus dem 19. Jahrhundert nötig sind.

Doch dieser Unfug ist normal. So beinhalten die Lehrprogramme der Segelschulen das Erlernen der Navigation mit dem Höhen differenzverfahren nach Hilaire. In einem Ernsfall wird damit keiner mehr zurechtkommen. Mit meinen Beiträgen will ich zeigen, dass es auch anders geht, dass auch zur Astronavigation niemand mehr auf See etwas berechnen oder zeichnen muss. Dieser Beitrag sollte vor allem zeigen, dass die mathematische Präzision alternativer Verfahren sogar besser ist, es darauf aber gar nicht ankommt, weil eine Standortabweichung in der astronomischen Navigation mit weniger als 10% von der mathematischen Genauigkeit einer Methode abhängt.