Mittagsbreite und Chronometerlänge

Inhalt

28. April 1789, die berühmteste Seereise der Welt. Captain Bligh von der Bounty kehrt nach 4000 sm in einer kleinen Barkasse in die Zivilisation zurück.

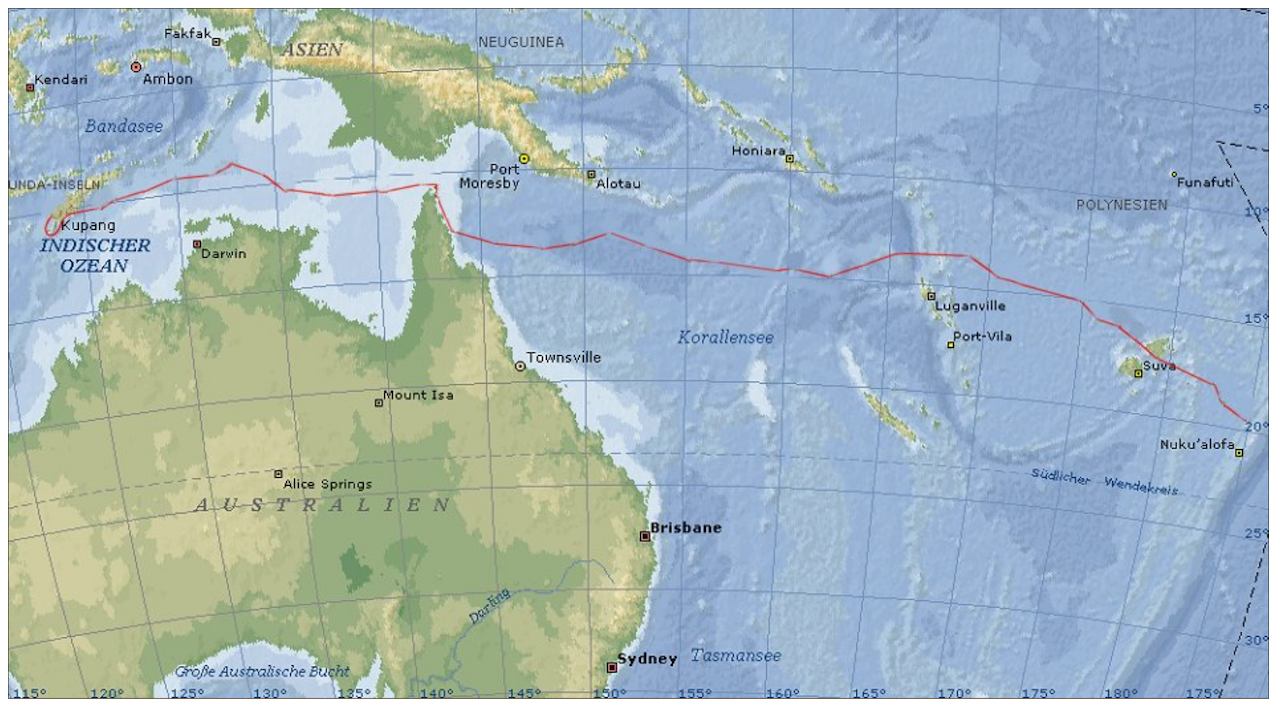
Der Beitrag behandelt einen kleinen Teil der sogenannten alten Methoden der Astronavigation. Es ist eine Einführung in ein Thema, das in früheren Jahrhunderten noch als Geheimwissenschaft gehandelt wurde. Ziel einer Standortbestimmung ist das Finden des Breiten- und Längengrades des eigenen Standortes. So hat James Cook im 18. Jahrhundert navigiert und die Küsten von Australien und Neuseeland erstaunlich genau vermessen. Erforderliche Hilfsmittel sind ein Chronometer (Quarzuhr), ein Sextant und das Nautische Jahrbuch. Ein Chronometer stand James Cook allerdings erst auf seiner zweiten Reise zur Verfügung. Bis dahin mußte er sich mit komplizierten Berechnungen auf der Grundlage von Monddistanzen zu bekannten Fixsternen herumschlagen, um die jeweilige Zeit am Greenwich Nullmeridian bestimmen zu können.

Zu den alten Methoden zählen aber auch alle algebraischen Methoden, so die in der Literatur am Ende des 18. Jahrhunderts mehrfach beschriebene Methode zur Berechnung der Breite direkt aus den Höhengleichen aber auch die Methode von Douwes oder die von Borda. Die Methode von Carl Friedrich Gauß ist eine analytische Methode und unterscheidet sich von den vorstehend genannten dadurch, dass ihr Ansatz zwar auf demselben geometrischen Modell beruht, der Lösungsweg selbst aber keinerlei geometrische Betrachtungen enthält, sondern eine reine mathematische Analysis ist. Deshalb wird seine Methode bis heute von Seefahrern nicht verstanden. All diese genannten Methoden waren mit einem sehr großen Rechenaufwand verbunden und haben sich deshalb in der Seefahrt nicht etablieren können.

Die Erfindung des Chronometers leitete mit dem Beginn des 19. Jahrhunderts eine ganz neue Entwicklung ein, die mit der Erfindung der Standlinie im Jahre 1843 durch Thomas Sumner ihren ersten Höhepunkt fand und den Auftakt für die Ära der sogenannten modernen Astronavigation gab, die erst mit dem Start der Satellitennavigation endete. Die alten algebraischen Methoden wurden durch die neue Astronomie, wie man sie damals bezeichnete, verdrängt und sind heute vergessen.

1 Nordsternbreite und Mittagsbreite

Die Bestimmung der Breite gehört zu den wichtigsten und zugleich ältesten Navigationsverfahren überhaupt. Als das Längenproblem noch nicht gelöst war hatten die Seeleute nur eine Chance ihr Ziel zu finden. Sie segelten an bekannten Küsten Breiten ab, bis die richtige Breite gefunden war und überquerten den Ozean dann stur dieser breite folgend. Doch wie bestimmten Sie die Breite?

Wie der Beitrag „Die Sonne am Himmel“ zeigt, ist der Winkel zwischen Gestirn und Zenit gleich der Entfernung zum Bildpunkt des Gestirns. Da man zum Zenit nicht messen kann, weil es da keine Markierung gibt, misst man die Höhe zwischen Gestirn und Kimm und zieht diesen Wert von 90° ab. Das Ergebnis ist dann die sphärische Entfernung (über die Erdrundung) zum Bildpunkt in Grad. Will man die Entfernung in Meilen haben, dann ist dieser Gradwert mit 60 zu multiplizieren, denn 1 Grad sind 60 Seemeilen. Wenn ein Gestirn genau im Süden oder genau im Norden beobachtet werden kann, dann befindet sich der eigene Standort auf genau demselben Meridian wie der Bildpunkt des Gestirns. Zur Bestimmung der Breite muss dann nur die Entfernung zum Bildpunkt gemessen und mit der Deklination des Gestirns verrechnet werden.

*Bild 1: Messung der Sonnenhöhe mit Jakobsstab. Bei ungeschützte Augen führte das auch zur Erblindung.*

Vor dem Sextanten war der Jakobsstab das gebräuchlichste Gerät zur Bestimmung der Gestirnshöhe über dem Horizont. Mit ihm konnte man die Höhe der Sonne oder des Nordsterns einigermaßen abschätzen, indem man einen Schieber ein Messlineal entlang schob, bis der Schieber ein genaues Maß zwischen Horizont und Sonne bildete. Bei der Sonne konnte man sich schon die Augen schädigen und deshalb wurde der Jakobsstab auch umgekehrt mit einem schwarzen Spiegel benutzt. Abgelöst wurde der Jakobsstab durch Oktanten und Sextanten.

Zur Bestimmung der Breite gibt es insbesondere zwei Möglichkeiten, die Nordsternbreite und die Mittagsbreite. Der Nordstern ist nur auf der Nordhalbkugel zu beobachten. Er ist nicht nur dazu geeignet, die Nordrichtung anzugeben. Eine Besonderheit besteht auch darin, dass seine Höhe über dem Horizont auch die Breite ist, auf der gesegelt wird. Eine Höhenmessung ist allerdings nur in der Dämmerung möglich, solange der Horizont noch sichtbar ist.

Der Nordstern steht allerdings nicht ganz exakt im Norden, sondern beschreibt im Laufe von 24 Stunden einen kleinen Kreis mit einem Durchmesser von weniger als 1°. Nehmen wir an, dass sein Licht senkrecht auf den Nordpol fällt und sein Bildpunkt damit der Nordpol wäre. Dann ist der Einfallswinkel seines Lichtes und somit seine Höhe über dem Horizont identisch mit der Breite, auf der man sich gerade befindet. Bei einem Standort direkt auf dem Nordpol würde seine Höhe mit 90° festgestellt werden, denn er stände dort im Zenit. Bei einem Standort am Äquator würde er, wenn überhaupt, bei 0° gesehen werden. Vernachlässigt man seinen kleinen Kreisdurchmesser von knapp 1°, dann führt das zu einer Abweichung in der Breite von ebenfalls knapp 1°, also 60 nm in Nord-Süd Richtung.

*Bild 2: Höhenmessung mit dem Oktant. ein Helfer stoppt die Zeit und notiert den abgelesenen Wert.*

Die Mittagsbreite zu bestimmen ist ein Ritual, das seit Jahrhunderten auf Seeschiffen abläuft. Der Navigator tritt am Mittag mit dem Sextanten, früher auch mit dem Jakobsstab oder Oktanten an Deck, um die Höhe der Sonne während ihrer Kulmination festzustellen. In dem Moment steht die Sonne über demselben Meridian wie das eigene Schiff und wird exakt im Süden (oder Norden) gesehen.
Man sollte ungefähr wissen, wann Schiffsmittag ist, um nicht so lange mit dem Sextanten auf der Lauer liegen zu müssen. Einige Minuten davor oder danach verändert sich die Höhe der Sonne nicht messbar. Man hat also Zeit, die Kulmination der Sonne beobachten zu können, kann bis zu drei Minuten Pause von Messung zu Messung verstreichen lassen.
Sobald die Kulminationshöhe feststeht, kann der Breitengrad mit Hilfe einer kleinen Rechnung bestimmt werden. Vorher muss man die abgelesene Höhe noch beschicken, um den Einfluß von Durchmesser der Sonnenscheibe, Refraktion und Standhöhe auszugleichen. Ein gutes Mittelmaß sind 13’, die zu einer Sextantenablesung addiert werden müssen, wenn der Unterrand der Sonne beobachtet wurde. Für die nachfolgende kleine Rechnung braucht man die Deklinationsbreite δ der Sonne. Diese konnte man einer Tabelle entnehmen. Später wurde die Deklination genauer in nautischen Jahrbüchern erfasst. Viel zu rechnen gibt es dabei nicht. Es gilt

bei Kulmination der Sonne im Süden: 90° – Höhe + Deklination,
bei Kulmination der Sonne im Norden: Höhe – 90° – Deklination .

Auch auf der Nordhalbkugel kann die Sonne im Norden kulminieren, wenn der Standort zwischen dem Äquator und der Deklinationsbreite liegt. Zu beachten ist, dass südliche Deklinationen mit einem negativen Vorzeichen gekennzeichnet sind. Nördliche Deklinationen und die Höhe bekommen ein positives Vorzeichen. Ein negatives Ergebnis weist also auf eine südliche Breite hin. Hierzu drei Beispiele:

Beispiel 1: Deklination δ = 21° N, h = 65°, Kulmination im Süden
Ergebnis: φ = 90° – 65° + 21° = 46° = 46° N

Beispiel 2: Deklination δ = 14° S, h = 53°, Kulmination im Norden
Ergebnis: φ = 53° – 90° -14° = -51° = 51° S

Beispiel 3: Deklination δ = 23° N, h = 84°, Kulmination im Norden
Ergebnis: φ = 84° – 90° + 23° = 17° = 17° N

Für die Berechnung der Grundmethoden Mittagsbreite, Mittagslänge und Chronometerlänge wurde ein kleines EXCEL Sheet zum Herunterladen erstellt.

basic-sun-navigator-4

Dieses EXCEL-Programm ist auch auf allen Mobilgeräten lauffähig, auf denen die EXCEL App installiert ist, also auch auf Smartphones. Die Version 4 arbeitet mit integrierter Berechnung der Sonnenpositionen. Ein nautisches Jahrbuch ist also nicht nötig.

1.1 Excel Sheet zur Mittagsbreite

Das Bild 3 zeigt einen Ausschnitt aus der Eingabenmaske des EXCEL-Sheets, der zur Bestimmung der Mittagsbreite vorgesehen ist. Eingaben können nur in den grau hinterlegten Feldern gemacht werden. Der blau umrandete Block dient zur Eingabe der Daten, die für eine Sextantenbeschickung gebraucht werden. Das sind die Augeshöhe in Metern, darunter eine Angabe darüber, ob die Sonne mit ihrem Oberrand „O“ oder wie meist üblich, mit ihrem Unterrand „U“ im Teleskop des Sextanten auf den Horizont gesetzt wird und nochmals darunter der Betrag zur Indexberichtigung. Die Indexberichtigung ist der Indexfehler mit umgekehrtem Vorzeichen. Wird also ein Indexfehler von 3,5′ festgestellt, dann ist als Indexberichtigung -3,5′ einzugeben. Insbesonders Plastiksextanten haben größere temperaturabhängige Indexfehler. Diese sollten vor jeder Messung neu festgestellt werden. Sextanten dürfen nicht in der Sonne liegen bleiben, weil sich dann ihre Messfehler stark verändern können.

Im darunterliegenden rot gerahmten Block werden Datum und Uhrzeit als UTC der Beobachtung eingegeben, wobei eine minutengenaue Zeit ausreicht. Daraus berechnet sich das Programm die Deklination selbst. Nach Eingabe der Sextantenablesung muss noch eingegeben werden, in welcher Himmelsrichtung, östlich oder westlich die Sonne gesehen wurde.

Bild 3: Eingabefelder in der EXCEL Datei zur Bestimmung der Mittagsbreite.

Die Feststellung der Kulmination erfordert immer etwas Zeit und mehre Messungen mit dem Sextanten. Man sollte die Kulminationszeit vorher schon einzuschätzen versuchen, damit man sich nicht allzu lange der Sonne aussetzen muss. Die Kulminationszeit vom Vortagkann dabei als Richtwert verwendet werden. Unmittelbar nach Eingabe aller Daten wird die Mittagsbreite in Grad und Minuten angezeigt. Durch Ortveränderung ändert sich die Breite und sollte deshalb für eine spätere Längenbestimmung gekoppelt werden.

2. Die Mittagslänge

Der Wunsch nach einer einfachen Methode zur Bestimmung der Länge, nur unter Anwendung der Grundrechenarten, führte insbesondere in der Szene der Blauwassersegler zur Bestimmung der sogenannten Mittagslänge. Das Verfahren hat keine historischen Wurzeln. Sein Hauptnachteil besteht in einem recht komplizierten Messvorgang mit dem Sextanten. Außerdem ist diese Länge nur einmal am Tag für den Moment des Schiffsmittags bestimmbar. Messfehler steigen mit größer werdender Entfernung zur Deklinationsbreite, wenn die Sonne zur Mittagszeit steht. Trotzdem soll dieses Verfahren vorgestellt werden, denn es hat eine Zeitlang unter Seglern eine Rolle gespielt.

Bild 3 zeigt den Tagbogen der Sonne. Ihre Höhe steigt am Vormittag beinahe linear an, geht kurz vor Mittag in einen Bogen über und fällt am Nachmittag wieder genauso linear ab. In den linearen Flanken kann ihr Kimmabstand immer auch einer angebbaren Zeit zugeordnet werden. Ganz anders am Mittag. Da scheint ihre Höhe minutenlang konstant zu bleiben. Etwa vier Minuten lang wird immer die gleiche Höhe festgestellt, doch in diesen Minuten legt ihr Bildpunkt dann eine Strecke von 1 Grad zurück, was einer Strecke von 60 Seemeilen entspricht. Es ist somit unmöglich, die Mittagshöhe direkt messen zu wollen, um daraus die Länge zu bestimmen. Genau das ist aber das Ziel, denn nur am Schiffsmittag befinden sich der Bildpunkt der Sonne und der Schiffsstandort auf demselben Meridian. Würde man die Kulminationszeit der Sonne, genau kennen, dann liefert das nautische Jahrbuch für diese Zeit mit dem Greenwichwinkel den Stundenwinkel für diesen Meridian. Stundenwinkel zählen von 0° bis 360°. Der Greenwichwinkel Grt kann aber ganz einfach in geografische Längen umgedeutet werden. Liegt dieser zwischen 0° und 180°, dann sind es Westgrade. Ist Grt größer als 180°, dann ist dieser Wert von 360° zu subtrahieren und das Ergebnis sind dann Ostgrade:

0° ≤ Grt ≤ 180° ➞ ergibt Westgrade
180° ≤ Grt ≤ 360° ➞ 360° – Grt ergibt Ostgrade

Bild 4: Bestimmung des Schiffsmittags durch Feststellung zweier Zeiten mit gleicher Höhe

Weil der Kulminatonszeitpunkt nicht direkt gemessen werden kann, muss dafür eine andere Methode gefunden werden. In dem Buch „Steuermannskunst“ von Arthur Breusing findet man dafür eine Anleitung. Man muss die Höhe der Sonne nur einige Zeit vor dem Kulminatinszeitpunkt messen und danach den Zeitpunkt erwischen, in dem die Sonne bei ihrem Abstieg wieder dieselbe Höhe hat. Diese Zeit sollte mit etwa 0,5 h bis 1,5 h bemessen werden. Je höher die Sonne je nach Jahreszeit und Standort steigen kann, desto kürzer kann diese Zeit angelegt werden.Wir haben jetzt zwei Zeiten. Die Zeit t₁ ist der Zeitpunkt der ersten Höhenmessung vor dem Mittag und zum Zeitpunkt t₂ wurde wieder dieselbe Höhe nach dem Mittag gemessen. Logischerweise ergibt sich daraus die genaue Mittagszeit t_M als arithmetischer Mittelwert:

$\begin{equation*} t_M=\frac{t_1+t_2}{2}\cdot\end{equation}$

Sollte die Zeit t₂ kleiner sein als die Zeit t₁, was beim Segeln an der Datumsgrenze geschehen kann, dann muss die Zeitsumme um 12:00 vergrößert werden. hier gilt dann:

$\begin{equation*} t_M=\frac{t_1+t_2+12:00}{2}\cdot\end{equation}$

Es gehört schon sehr viel Übung dazu, die Zeit t₂ zu finden, in der die Sonne den Horizont berührt. Man hat im Gegensatz zur ersten Messung nur einen Versuch dazu. Der Sextant muss wie bei der ersten Messung senkrecht stehen, was durch Schwenken erreicht wird. Es kann auch passieren, dass bei der zweiten Messung die Sonne von Wolken verdeckt ist. Dann ist es hilfreich, wenn mindestens eine oder sogar mehrere erste Messungen auf Vorrat gemacht worden sind. Eine Beschickung des am Sextanten abgelesenen Wertes darf nicht erfolgen. Der Sextant muss sich bei beiden Messungen auf gleichem Temperaturniveau befinden. Gerade Plastiksextanten sind sehr temperaturempfindlich und ihr Gebrauch bei unterschiedlichen Temperaturen kann leicht zu Messfehlern führen. Den Sextanten legt man nach der ersten Messung am besten gleich an seinen üblichen Aufbewahrungsort zurück, wo sich seine Temperatur nicht mehr ändern kann.

2.1 Excel Sheet zur Mittagslänge

Das Excel-Sheet basic-sun-navigator hat auch dafür eine Hilfe, die im Bild 5 gezeigt wird. Das Datum ist dasselbe, das im Modul zur Bestimmung der Mittagsbreite eingegeben wird. Ansonsten ist das Eingabemenü sehr übersichtlich. Hier erfolgten zwei Vormittagsmessungen um 10:46:33 UTC und um 10:54:23 UTC, wobei die zweite nur eine Vorratsmessung ist. Der dabei gemessene Kimmabstand ist in dem Feld darüber eingetragen. Sobald die Zeit der zweiten Messung festgestellt und eingetragen ist, werden die Zeit des Schiffsmittags und auch gleich die Mittagslänge angezeigt.

Bild 4: Eingabefelder in der EXCEL Datei zur Bestimmung der Mittagslänge.

Zusammen mit der Mittagsbreite liegt jetzt bereits ein Standort fest, der aber nur genau wäre, wenn mit dem Schiff keine Ortsveränderung, Versegelung genannt, erfolgt wäre. Außerdem kann dieser Standort nur einmal am Tag erzeugt werden. Da man jedoch nicht auf der Stelle dümpelt, muss bei dieser Methode mit Fehlern gerechnet werden. So bleibt als einziger Vorteil, dass selbst ohne Excel-Unterstützung nicht viel gerechnet werden muss. Eine bessere Art der Längenbestimmung, die jedoch mit etwas Mathematik verbunden ist, ermöglichte die Erfindung des Chronometers durch John Harrison, der wir uns nun zuwenden wollen.

3. Die Chronometerlänge

Die geografische Breite war also als Mittagsbreite relativ einfach und mit hoher Genauigkeit bestimmbar. Eine aktuelle Breite konnte durch Koppeln gefunden werden. Dagegen galt die Bestimmung des Längengrades über einen Zeitraum von 400 Jahren als unmöglich.
So war es üblich, dass die Schiffe in bekannten Gewässern an einer Küste entlang wochenlang Breiten absegelten, bis die gewünschte Breite erreicht war. Erst dann konnten sie den Breitenkreis entlang eine Überfahrt zu einem bekannten Hafen antreten. Zahlreiche Schiffe gingen verloren, weil sie sich in der Länge verschätzten und früher als gedacht an Land gerieten. Monatelange Fahrten ohne frische Lebensmittel und Wasser rafften die Mannschaften durch Skorbut dahin. Das sogenannte Längenproblem wurde zunehmend zu einem wirtschaftlichen Problem.

Bereits 1600 setzte der spanische König ein Preisgeld aus, um das Längenproblem lösen zu können, doch er blieb damit erfolglos. Mehr als hundert Jahre später, im Jahre 1714, folgte das englische Parlament diesem Beispiel und setzte bis zu 20 000 Pfund Preisgeld für eine praktikable Lösung des Längenproblems aus. Anlass war der Untergang von vier Schiffen 7 Jahre vorher, die auf den Klippen der Skilly-Inseln zerbrachen und dem etwa 1500 Seeleute zum Opfer fielen. Das Preisgeld war aufgestaffelt nach Genauigkeit: 10 000 Pfund für 1° Präzision, 15 000 Pfund für 40′ Präzision und 20 000 Pfund für 30′ Präzision.

Erst zehn Jahre später beschäftigte sich John Harrison damit. Er war eigentlich Tischler, hatte aber bereits eine Uhr mit Holzzahnrädern gebaut und ihn ließ die Vision nicht mehr los, eine genau gehende Schiffsuhr zu bauen. Damals gab es zwar schon Verfahren, wie die Länge aus der Bedeckung der Jupitermonde oder des Abstands unseres Erdmondes hergeleitet werden konnte, aber diese Verfahren waren an Bord der üblichen Schiffe nicht praktikabel, denn sie waren viel zu selten. Man brauchte praktikablere Methoden.

*Bild 5: Die H5, ein verbessertes Exemplar, das John Harrison erst drei Jahre vor seinem Tod fertigstellte.*

Mit einem ersten Uhrenexemplar von Harrison gelang eine Testfahrt, bei der die Genauigkeit der Methode bestätigt werden konnte. Das Preisgeld wurde jedoch nicht gezahlt, weil die Testreise nicht ganz den Anforderungen entsprach. Es könnte auch alles Zufall gewesen sein, meinten einige Kritiker. Außerdem gab es Widerstände und Bedenken. Die Zuverlässigkeit eines technischen Instrumentes wurde angezweifelt. Insbesondere vom Hofastronom des englischen Königshauses, Nevil Maskelyne, der auf die Monddistanz Methode setzte, weil sie unabhängig von technischen Instrumenten ist. Hier könnte man an die jüngere Geschichte erinnert sein. Sogar der Taschenrechner hatte es einst schwer, in der Astronavigation die Logarithmen zu verdrängen.

Erst als James Cook 1775 von seiner zweiten Weltreise zurückkehrte und die gute Qualität eines heute mit H4 bezeichneten Modells eines Harrison Chronometres bestätigte, galt auch in Astronomenkreisen das Längenproblem als gelöst. Harrison wurde ein Preigeld von 10 000 £ zugesprochen. Eine Weiterentwicklung, heute mit H5 bezeichnet, wurde von König Georg III persönlich getestet. Dafür erhielt Harrison weitere 8 750 £.

Nach der H5, die damals etwa 500 £ kostete, bauten Uhrmacher die Modelle nach und die Preise sanken. Die ersten in Serie produzierten Marine Chronometer waren schon 1790 verfügbar. Welche Bedeutung sie hatten zeigt die Tatsache, dass die Beagle auf ihrer Forschungsreise gleich 22 Stück davon an Bord hatte. Mitte des 19 Jahrhunderts waren schon viele seegehende Schiffe mit zwei Chronometern ausgestattet und der Kapitän besaß noch sein eigenes.

*Bild 6: Zeitball auf dem Royal Observatorium Greeenwich. (Link)*

Doch wie wird die Länge mit Hilfe eines Chronometers überhaupt bestimmt? Die Sonne legt in einer Stunde 15° zurück. Das ist ihre Winkelgeschwindigkeit. Wenn man an Bord auf einem Chronometer 14:00:00 GMT (Greenwich Mean Time) ablesen würde und die Ortszeit auf dem Schiff wäre 16:00:00 Uhr, dann wäre die Sonne noch 2 Stunden östlich vom eigenen Standort. In Grad umgerechnet ist die Sonne also schon 2 h, das entspricht 30° westlich von Greenwich und erreicht den Meridian des Schiffsortes, wenn sie diese 30° zurückgelegt hat. Die Standortlänge sollte also 60° W sein. Das stimmt allerdings nicht, denn hier ist noch die Zeitgleichung zu berücksichtigen. Die Sonne passiert den Greenwicher Nullmeridian nur viermal im Jahr genau um 12:00:00 GMT und sonst bis zu einer Viertelstunde früher oder später. Man müsste also die Summe von Chronometerzeit und Zeitgleichung, die in Tabellenform für jedes Jahr herausgegeben wird, mit der Winkelgeschwindigkeit der Sonne multiplizieren, um die Schiffslänge zu erhalten.
Das ist formal richtig, hat aber einen Haken und der besteht darin, dass die Bordzeit oder Ortszeit nicht bekannt ist. Eine Ortszeituhr gibt es leider nicht. Wie der Name schon sagt, ändert sich die Ortszeit nicht nur mit dem Gang der Sekunden, sondern auch mit der Ortsveränderung eines segelnden Schiffes. Auf den Fahrten zum Test der Harrison Chronometer waren deshalb auch immer Astronomen an Bord, die die Ortszeit feststellen mussten. Diese wurde durch Messung der Höhe eines Gestirns, beispielsweise der Sonne, mit Hilfe des nautischen Dreiecks errechnet.

Die Lage des Nullmeridians, auf den sich die Zeiten beziehen, ist willkürlich. In der Antike lief er durch die Kanaren, weil sie die am weitesten westlich liegenden bekannten Landteile waren. Die Franzosen ließen ihn durch Paris laufen und die Engländer durch den Londoner Stadtteil Greenwich. Auf der internationalen Meridiankonferenz 1884 in Washington, D. C. einigte man sich auf den Verlauf durch Greenwich. Anteil daran hatten die vielen von Nevil Maskelyne herausgegebenen Almanache und Monddistanz Tabellen, die sich alle auf Greenwich bezogen und nach denen die Mehrzahl der Schiffe aller Nationen bereits navigierten. Nur die Franzosen behielten ihren Nullmeridian durch Paris noch einige Jahre.

Eine Schwierigkeit bestand darin, dass die Chronometer nach langen Fahrten immer mal justiert werden mussten. Befand man sich an einem Ort, dessen Position bekannt war, dann konnte man dessen Ortszeit durch eine Höhenmessung bestimmen und diese Zeit unter Verwendung der Ortslänge auf GMT zurückrechnen. Möglich war auch eine Zeitbestimmung durch Messung einer Monddistanz. In verschiedenen Häfen gab es auch Zeitbälle. Der Ball wurde an einem Mast hochgezogen und zu einer bestimmten Zeit wieder fallen gelassen. Im Royal Observatorium Greenwich geschah das um 1:00:00 GMT. Die Bälle waren so positioniert, dass sie weithin sichtbar waren, auch für die Schiffe, die noch am Anker lagen. Das erleichterte das Stellen der Uhren. Mit dem Aufkommen des Seefunks gab es dann Zeitzeichen und die Bälle wurden fast überall wieder abgebaut.

3.1 Berechnung am Nautischen Dreieck

Die Methode der Chronometerlänge verbreitete sich rasch, hatte allerdings auch ihre Schwachstellen. Ihre Genauigkeit hing ja nicht nur von der Ganggenauigkeit des Chronometers ab, sondern auch von der Standortbreite. Diese wurde nämlich zu einem ganz anderen Zeitpunkt bestimmt, und in der Zwischenzeit konnte eine erhebliche Änderung in der Breite eingetreten sein. Die getrennte Bestimmung der Ortskoordinaten, Länge und Breite, war jedoch charakteristisch für die damalige Zeit und wurde erst ab Mitte des 19. Jhd. von der sog. modernen Astronavigation abgelöst.

Bild 7 zeigt das nautische Dreieck in zwei unterschiedlichen Konstellationen. Die Ecken der Dreiecke werden gebildet von Z, dem Standort des Schiffes, dem Bildpunkt X der Sonne oder eines anderen Gestirns und N einem Pol, im Beispiel dem Nordpol. Die Dreieckseiten sind mit s, p und b bezeichnet. Diese Seiten sind die Komplemente von Gestirnshöhe, Deklination und Standortbreite. Unter Komplement wird die Differenz eines Winkels zu 90° verstanden. Komplemente erleichtern das Schreiben der Gleichungen ganz erheblich. In der folgenden Tabelle sind die Dreieckseiten und ihre zugehörigen Komplemente definiert: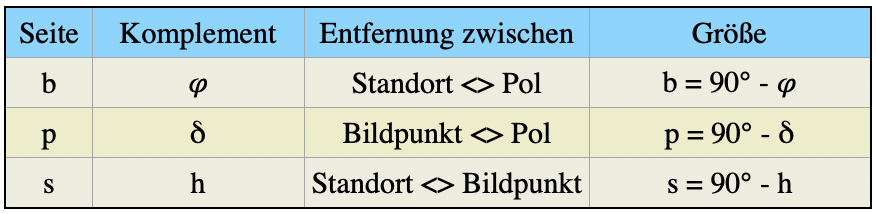

Bild 7 zeigt, dass eine Standortlänge bequem aus dem Greenwicher Stundenwinkel Grt und dem Polwinkel $\tau$ berechnet werden kann. Auf der linken Seite des Bildes ist es einfach die Summe Grt + $\tau$ , weil die Sonne vom Standort aus östlich gesehen wird und auf der rechten Seite ist es die Differenz Grt – $\tau$ , weil die Sonne im Westen der Beobachterposition steht. Man muss also nur den Polwinkel tau berechnen.

*Bild 7: Zwei Konstellationen nautischer Dreiecke, wie sie zur Bestimmung der Chronometerlänge benutzt werden.*

Der Kosinus Seitensatz, die Geheimwaffe der Astronavigation, lautet für diesen Fall:

$\begin{equation*}\cos s =\cos p\cdot \cos b+\sin p\cdot \sin b\cdot \cos \tau\end{equation}$

Nach Umstellung auf die Winkelfunktion $\cos \tau$ und Benutzung der Komplemente in aufeinanderfolgenden Schritten folgt daraus:

$\begin{equation*}\cos\tau=\frac{\cos s-\cos p\cdot \cos b}{\sin p\cdot \sin b}=\frac{\sin h-\sin \delta\cdot \sin \varphi}{\cos \delta\cdot \cos \varphi}\end{equation}$

Schließlich wenden wir noch die Umkehrfunktion an, um aus der Winkelfunktion den Winkelwert zu erhalten:

(1) $\begin{equation*}\tau=arccos\frac{\sin h-\sin \delta\cdot \sin \varphi}{\cos \delta\cdot \cos \varphi}\end{equation*}$

Zur Chronometerlänge ist es jetzt nur noch ein kleiner Schritt:

(2) $\begin{equation*}\boxed{\lambda^\ast=Grt\pm\tau}\end{equation*}$

Das Sternchen besagt nur, dass die berechnete Länge nicht in das Gradsystem der Erde mit 180 Ostgraden und 180 Westgraden passt und deshalb eine Umrechnung erforderlich ist. Das ist in ähnlicher Weise auch schon vorstehend bei der Umrechnung von Grt in geografische Grade nötig gewesen. Ob Grt und $\tau$ addiert oder $\tau$ von Grt subtrahiert werden muss, hängt davon ab, ob die Sonne östlich oder westlich beobachtet wird. Wenn die Höhe der Sonne am Vormittag gemessen wurde, dann muss addiert werden.

3.2 Chronometerlänge mit dem Excel Sheet

Ganz einfach geht die Bestimmung der Chronometerlänge mit Hilfe der EXCEL Datei. Bild 8 zeigt dafür die Eingabefelder auf der linken Seite. Vorangestellt ist wieder ein Block, in den die Daten zur Sextantenbeschickung eingegeben werden müssen. Es könnten Veränderungen nötig sein. Beispielsweise könnte der untere Sonnenrand von Wolken verdeckt sein und muss von „U“ auf „O“ gewechselt werden.

Das Datum wird aus dem Modul zur Mittagsbreitenbestimmung entnommen und kann deshalb auch nur dort geändert werden. In den darunter angeordneten Feldern sind dann die folgenden Angaben zu machen

Uhrzeit ➞ Die sekundengenaue Zeit in UTC, in welcher der vorgegebene Rand der Sonne im Teleskop des Sextanten auf den Horizont gesetzt wurde.
Breite ➞ Die seit der letzten genau bekannten Breite, z. B. Mittagsbreite, gekoppelte Breite (DR Latitude).
Höhe ➞ Einzugeben ist der auf dem Sextanten abgelesene Höhenwinkel. Die Sextantenbeschickung wird automatisch vom Modul vorgenommen.

Nach Eingabe dieser Daten gibt das Modul die berechnete Standortlänge in Grad und Minuten aus.

Bild 8: Eingabemaske des EXCEL Programms zur Längenbestimmung mit dem Chronometer

Seit der Heimkehr von James Cook 1875, der mit dieser Art der Längenmessung die Inselwelt des Pazifik erstaunlich genau vermessen hat, verbreitete sich die Methode weltweit mit steigender Verfügbarkeit von Chronometern. So war es nur eine Frage der Zeit, bis zur Erfindung der Standlinie 1837 durch Thomas H. Sumner. Aus heutiger Sicht erscheint uns der Weg von der Chronometerlänge zur Standlinie als logische Konsequenz, denn die Berechnungen sind absolut gleich. Nach der Erfindung des Chronometers musste jedoch fast ein halbes Jahrhundert vergehen, bis jemand wie Kapitän Sumner diesen Schritt machte und damit eine ganz neue Ära in der astronomischen Navigation begründete.

3.3 Von der Chronometerlänge zur Standlinie

Zur Berechnung der Chronometerlänge ist eine Standortbreite nötig und die kann nur geschätzt werden. In der Praxis wurde aus der Ortsveränderung nach einer Mittagsbreitenbestimmung eine Breitenkomponente hergeleitet und zur Mittagsbreite addiert. Das Ergebnis ist die sogenannte Koppelbreite oder DR Latitude (DR = Dead Reckoning). Man kann sich dabei aber leicht verschätzen, denn Winde und Meeresströmungen können das Schiff versetzen. Genau diese Gefahr sah Thomas Sumner auf seiner Fahrt zwischen Irland und England und er bestimmte die Chronometerlänge zur Sicherheit gleich drei Mal mit jeweils um 10′ gestaffelten Breiten, aber identischen Werten von Zeit und Höhe aus nur einer einzigen Beobachtung.

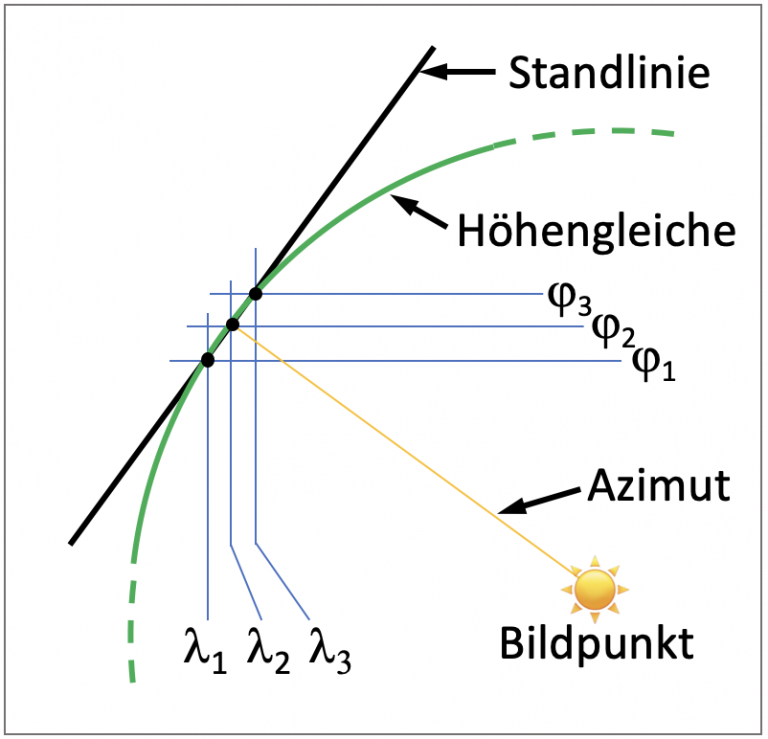
Bild 9: Bildung einer Sumner Line als Gerade durch drei Chronometerlängen auf drei geschätzten Breiten.

Sumner errechnete aus den drei Breiten φ1, φ2 und φ3 drei verschiedene Chronometerlängen λ₁, λ₂ und λ₃. Dies ergab drei mögliche Standorte aus den den Kreuzungen der vorgegeben Breiten mit den daraus berechneten Längen. Diese im Bild 9 als schwarze Punkte gekennzeichneten Standorte lagen in der Seekarte von Sumner in einer geraden Linie, was für große Verblüffung sorgte. Natürlich war die Höhe nur einmal gemessen worden und so ist die Entfernung von jedem der drei Orte zur Sonne gleich groß. Man könnte auch unendlich viele Berechnungen für alle Breiten machen. Alle dadurch errechneten Standorte würden dann auf der Kreislinie der Höhengleichen liegen.

Kapitän Sumner brauchte sechs Jahre, um seine Entdeckung in einem Buch zu veröffentlichen. Er erkannte, dass es nur einer einzigen Höhenmessung bedarf, um mit zwei geschätzten Standortbreiten eine Standlinie zu erzeugen, indem man durch die beiden möglichen Standorte eine Linie zieht Der Begriff Standort wurde durch den Begriff Standlinie konkreter, denn irgendwo auf dieser Linie befindet sich das Schiff. Das war aber nicht alles. Aus der Standlinie können Kurse auf ein Ziel oder sicher an einer gefährlichen Küste entlang abgeleitet werden. Zwei Standlinien, die zu verschiedenen Zeiten aus zwei Beobachtungen erzeugt werden, kreuzen sich, und weil der Standort auf jeder Linie irgendwo sein kann, ist der Kreuzungspunkt der konkrete Standort eines Schiffes.

Es war eine Revolution in der Hochseenavigation. Der Fregattenkapitän Saint Hilaire verbesserte 40 Jahre später die Konstruktion der Standlinie dadurch, dass er die Sehnenkonstruktion von Sumner durch eine Tangentenkonstruktion ersetzte. Dadurch konnte die Genauigkeit verbessert werden. Das Verfahren von Hilaire wurde erst von der Satellitennavigation abgelöst.

3.4 Sumner Standlinie mit dem Excel Sheet

Mit der Excel Datei basic_sun_navigator kann neben der Bestimmung der Chronometerlänge auch eine Sumner-Standlinie erzeugt werden. Das entsprechende Diagramm zeigt Bild 10.

Bild 10: Sumnerlinie für die im Bild 8 gezeigten Daten und drei Breiten: Schätzbreite ± Eingabewert

Der einzige Nachteil einer Sumner-Linie gegenüber einer Hilaire-Standlinie besteht darin, dass es eine Sekantenkonstruktion ist, während Hilaire eine Tangentenkonstruktion zum Ziel hat. Dieser Nachteil ist dadurch bedingt, dass es sich um eine grafische Konstruktion handelt, die früher mit Bleistiftlinien direkt auf der Seekarte ausgeführt wurde. Da musste man die zwei Chronometerlängen einer einzigen Höhenmessung auf zwei Breitenschätzungen legen, die weit genug auseinanderliegen. Nur dann ist es möglich, die zwei Punkte mit einer Linie im richtigen Winkel zu verbinden. Lägen die Punkte zu dicht beieinander, wäre das nicht möglich. Deshalb ist die Sumner Standlinie eine Sekante. Die Computertechnik erlaubt jedoch extrem dicht beieinander liegende Standorte durch extrem dicht benachbarte Schätzbreiten und damit Standlinien quasi als Tangenten im exakt richtigen Winkel.

Bild 10 zeigt eine Sumner Linie, die auf der Chronometerlängenberechnung nach dem Beispiel aus dem Bild 8 erzeugt wurde. Oberhalb des Diagrams befindet ich das Eingabefeld für die gegisste Breite. Das Modul berechnet im Hintergrund die Chronometerlänge für zwei weitere Breiten, die sich von der gegissten Breite um den eingegebenen Betrag unterscheiden. Im Bild 10 sind es ±10′ Unterschied zur Schätzbreite. Je kleiner der eingegebene Wert ist, desto mehr wird die Sekante zur Tangente und umso genauer wäre ein mit zwei Standlinien gefundener Standort, der dann sogar den Vorteil aufweist, dass es mit dieser Methode keine Höhenbegrenzung mehr gibt. Das ist ein Beispiel dafür, dass mit heutiger Rechentechnik das ältere Verfahren von Sumner gegenüber dem Verfahren von Hilaire im Vorteil ist. Mit Taschenrechnern wäre der Rechenaufwand mit nur einer Formel dann auch nur halb so groß und in einem Computerprogramm könnte sogar die Angabe einer Schätzbreite entfallen.

Wird in der Zeit zwischen zwei Messungen gesegelt, dann muss die erste Standlinie parallel verschoben werden und zwar in Kursrichtung um die gefahrene Strecke. Diese Navigationsmethode war in der zweiten Hälfte des 19. Jahrhunderts eine Standardmethode zur Positionsbestimmung auf See und sogar verbindlich für die Amerikanische Marine.

4 Klassische Berechnung der Chronometerlänge

Als es noch keine elektronischen Rechenmaschinen gab, musste das Navigieren ja auch irgendwie funktionieren. Damals gab es Logarithmentafeln, aber wie ging man damit um? Was Logarithmen sind, haben viele inzwischen schon vergessen. Wir wissen vielleicht noch, dass damit Multiplikationen und Divisionen auf Additionen und Subtraktionen zurückgeführt werden können. Logarithmen sind bekanntlich die Exponenten einer Basiszahl. Als Basis wird meist die Zahl 10 benutzt. So ist der Logarithmus von 100 die Zahl 2, weil die Basis² = 100 ist. Der Logarithmus von 1.000 ist dann 3, denn Basis³ ist 1.000 und wenn diese Logarithmen addiert werden, dann kommt 2 + 3 = 5 heraus und das ist eine 1 mit fünf nullen, also 100 mal 1000. Logarithmen sind in der Regel gebrochene Zahlen. So ist der Logarithmus von 27,47894 die Zahl 1,439, weil 10^1,429 = 27,47894 ist. Mit Logarithmen rechnet man in einem sogenannten Bildbereich und das ist einfacher. Am Ende muss das Ergebnis in den Originalbereich zurück transformiert werden. Zum hin- und her Transformieren stand diverses Tafelmaterial zur Verfügung. So wurden auch Logarithmen von Winkelfunktionen tabelliert, z. B. lg sin 45,8° = -0,14454.

Um ohne Unterbrechung optimal mit Logarithmen rechnen zu können, sollte in den Gleichungen nur multipliziert oder dividiert werden. Damit bleibt man im Bildbereich, wo man nur addieren und subtrahieren muss. Der Kosinus Seitensatz muss deshalb so verändert werden, dass in der Hauptgleichung nur noch multipliziert oder dividiert werden muss. In der Gleichung zur Bestimmung der Chronometerlänge

(3) $\begin{equation*}\cos\tau=\frac{\cos s-\sin \delta\cdot \sin \varphi}{\cos \delta\cdot \cos \varphi}\end{equation*}$

subtrahieren wir auf beiden Seiten eine 1:

$\begin{equation*}\cos \tau-1=\frac{\cos s -\sin \varphi\cdot \sin \delta}{\cos \varphi\cdot \cos \delta}-\frac{\cos \varphi\cdot\cos \delta}{\cos \varphi\cdot\cos \delta}\end{equation}$

Damit erhalten wir:

(4) $\begin{equation*}\cos \tau-1=\frac{\cos s -(\cos \varphi\cdot \cos \delta+\sin \varphi\cdot \sin \delta)}{\cos \varphi\cdot\cos \delta}\end{equation*}$

Ein Additionstheorem der trigonometrischen Funktionen lautet:

$\begin{equation*}\cos \alpha\cdot \cos \beta+\sin \alpha\cdot \sin \beta=\cos (\alpha-\beta) \end{equation}$

Damit vereinfachen wir den Klammerausdruck im Zähler der Gl.4 und erhalten:

(5) $\begin{equation*}\cos \tau-1=\frac{\cos s -\cos (\varphi-\delta)}{\cos \varphi\cdot\cos \delta}\end{equation*}$

Der Zähler dieser Gleichung kann jetzt mit einer sogenannten Verwandlungsformel aus dem Formelbuch umgestellt werde. Diese Verwandlungsformel lautet:

$\begin{equation*}\cos \alpha-\cos \beta=-2\cdot\sin \frac{\alpha+\beta}{2}\cdot\sin \frac{\alpha-\beta}{2}\end{equation}$

Nach ihrer Anwendung erhalten wir schließlich den völlig umgeformten Kosinus Seitensatz, der für die Berechnung mit Logarithmen optimal ist. Er lautet:

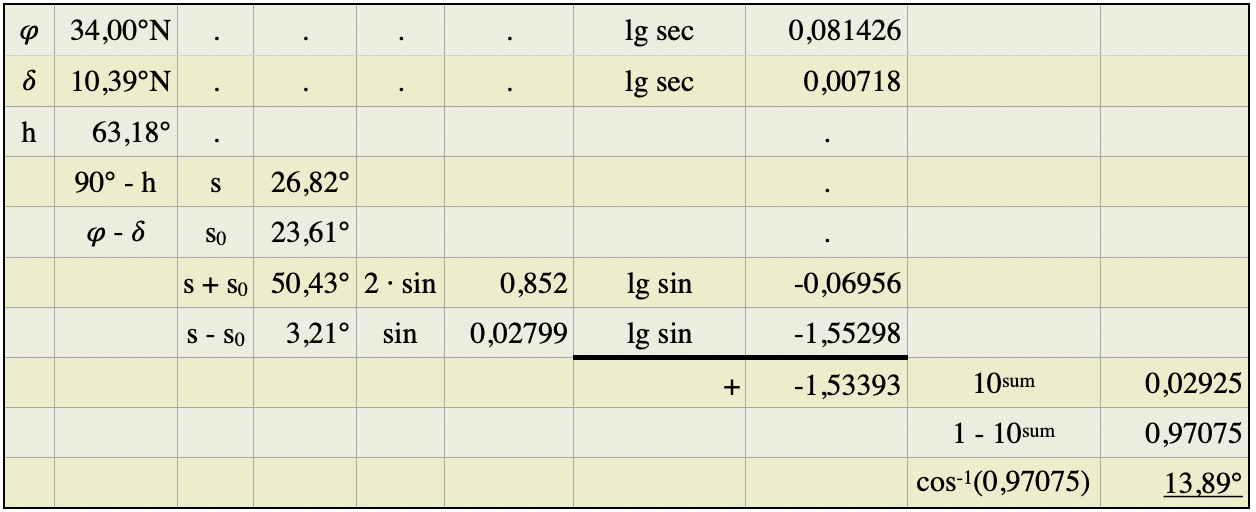
(6) $\begin{equation*}\cos \tau=1-\frac{2\cdot\sin \frac{s+s_0}{2}\cdot\sin \frac{s-s_0}{2}}{\cos \varphi\cdot\cos \delta}\end{equation*}$

In dieser Gleichung sind s = 90° – h der Zenitabstand und $s_0=\varphi-\delta$ die sog. Meridiandistanz. letzteres ist die algebraische Differenz zwischen Breite und Deklination, so wie sie am Schiffsmittag herrscht. Besitzen sie ein gleichnamiges Vorzeichen, dann sind sie zu subtrahieren. Bei ungleichnamigem Vorzeichen sind sie zu addieren. Zum Schluss soll dafür noch ein Beispiel berechnet werden. Dafür werden die Zahlen aus dem obigen Beispiel verwendet.

In dieser Tabelle sind die logarithmierten Sekanten jeweils die Logarithmen des Kehrwertes der Kosinusfunktionen der Winkel, also lg(1/cos $\varphi$ und lg(1/cos ∂). Dadurch können alle Logarithmen addiert werden.
Der Polwinkel von 13,89° bzw. 13° 53,47′ ist der Winkel, bzw. die Länge, den der Bildpunkt der Sonne noch bis zum Schiffsmittag zurücklegen muss. Ein Greenwicher Stundenwinkel Grt stand in damaligen Tabellen nicht zur Verfügung, nur eine Tabelle mit der Zeitgleichung und die hatte am 16. April 2020 nur einen Wert von 18,4 Sekunden.

Wie auf klassische Art aus dem Polwinkel die Länge berechnet wurde, zeigt die nachstehende Tabelle, die einem alten Lehrbuch entlehnt worden ist. Indem wir zunächt den Polwinkel von 13,89° aus obiger Tabelle durch 15°/h teilen, erhalten wir die Zeit bis zum Schiffsmittag und die beträgt hier 0,926075 h bzw. 00:55:34 h. Den Rest zeigen die weiteren Tabellenzeilen b bis g.

Die berechnete zeitlichen Entfernung des Standortes vom Londoner Stadtteil Greenwich von 00:51:56 h kann jetzt durch Multiplikation mit 15°/h die Entfernung in Grad umgerechnet werden und liefert die Länge des Standortes mit 12° 59,00′ W.

Neben der hier vorgestellten Methode gibt es noch eine ältere und sogar noch etwas einfachere Methode zur logarithmischen Berechnung der Chronometerlänge. Sie beruht auf der logarithmischen Berechnung der Länge bereits mit der Gl. 5. Diese Methode hat Kapitän Sumner im Zusammenhang mit seiner Methode in seinem Buch vorgestellt. Sie wird in dem Beitrag dazu erläutert.

Unter Verwendung des Grt bzw. GHA, wie das dann später üblich wurde war die Rechnung sehr viel einfacher. Den Grt lieferte ein nautischer Almanach. In diesem Beispiel müssen wir ihn aber selbst berechnen. Er ergibt sich als Stundenwinkel von Chronometerzeit, Zeitgleichung und 12^h, was dann 23:56:22^h sind und mit 15°/h einen Grt von 359,0917° ergeben. Da die Beobachtung noch vor dem Mittag erfolgte, ergibt sich die Standortlänge dann als Summe von Grt und Polwinkel mit 359,0917° + 13,892° = 372,8937°. Da hier wegen des Überlaufs 360° abgezogen werden müssen, ist es eine Westlänge und die beträgt dann genau 12,9837° W oder 12° 59,02′ W.

Links:

nach oben ♦ Die Sonne am Himmel ♦ Gauß und das Zweihöhenproblem ♦ Thomas H. Sumner, Begründer der Standliniennavigation ♦ Die Methode des Marcq Saint Hilaire ♦ Navigieren mit Excel ♦ Ein wenig Sextantenkunde ♦ Sextantentest Mark 25 ♦ Downloads ♦ Home