Vor 500 Jahren navigierte Fernando de Magallan als erster Seefahrer rund um die Welt
Die Höhenmethode von Saint Hilaire ist seit 1875 bekannt und galt bis zur Einführung der Satellitennavigation weltweit als Standardmethode in der astronomischen Navigation. Danach sollte sie eine Rückfallmethode für den Fall sein, dass Satellitennavigation aus irgend einem Grunde nicht benutzt werden kann.
Es war eine geniale Leistung von Saint Hilaire, einen Weg gefunden zu haben, an die Kreislinie einer Höhengleiche fast genau im Standort eine Tangente zu konstruieren. Von dieser Leistung hat die Seeschifffahrt mehr als ein ganzes Jahrhundert profitieren können. Auf der Grundlage dieser Methode entstanden später sogar Tabellenbücher mit vorausberechneten Daten, so dass eine Standortbestimmung ohne komplizierte Formeln erledigt werden konnte. Nach dieser Tafelmethode haben auch Flugzeuge navigiert.
Ein Nachteil der Sumer Methode
Die Sumner Methode verbreitete sich in der zweiten Hälfte des 19. Jhd. recht schnell, war sie doch die einzig bekannte Möglichkeit, auf dem Meer ohne Landsicht die eigene Position finden zu können.

Die Wahl von zwei ganzzahligen Breiten, zwischen denen der Schiffsort vermutet wird, war ein Kompromiss, der das Rechnen erleichtern und gleichzeitig eine grafische Linienkonstruktion ohne größere Winkelfehler auf der Seekarte ermöglichen sollte. Genau darin lag jedoch ein Nachteil der Methode. Der Abstand zwischen zwei ganzzahligen Breiten ist mit 60 NM recht groß und damit bildeten die Kreisbögen der Höhengleichen Erhebungen über den Standlinien. Bild 1 zeigt das in übertriebener Weise. Die Sumnerlinien sind Sekanten an den Höhengleichen. Der wahre Standort ist aber der Schnittpunkt der Höhengleichen und nicht der Schnittpunkt der Sekanten. Die Frage war, wie dieser Fehler vermieden werden kann.
Offenbar wird der Fehler kleiner, wenn die Sekanten näher an die Kreislinie geschoben werden könnten. Das kann dadurch erreicht werden, dass der Abstand zwischen den zu schätzenden Breiten kleiner gewählt wird, beispielsweise nur 6 NM. Dass der Schiffsort dann nicht mehr zwischen den gewählten Breiten liegen würde, wäre nicht mal das Problem, denn die Sumnerlinien können sich auch außerhalb der gewählten Breiten kreuzen. Durch die enger zusammenliegenden Breiten liegen dann aber auch die berechneten Längen sehr dicht zusammen und es wird nicht mehr möglich sein, eine Sumnerlinie im richtigen Winkel durch zwei dicht beieinander liegende Bleistiftpunkte zu ziehen. Die Grenzen grafischer Lösungen sind eben begrenzt
Die bessere Standlinie
Diese Überlegungen mag wohl Saint Hilaire angestellt haben, als er sich zur Aufgabe machte, das Sumnerverfahren so zu modifizieren, dass es optimal in einer zeichnerischen Navigation verwendet werden kann. Die größte Höhe des Kreissegmentes, der Punkt, an den die Sekante verschoben wurde, muss aber nicht der wahre Standort sein. Von den beiden bei Sumner zu schätzenden Breiten kann die eine näher und die andere weiter weg vom wahren Standort liegen.
Zu jener Zeit galt der Sumner Methode ein großes Interesse und es wurde darüber diskutiert, wie sich Fehler in der beobachteten Höhe, egal woraus diese resultieren, korrigiert werden können. Darüber veröffentlichte Hilaire im Oktober des Jahres 1873 in einem Artikel eine Notiz. Diese lautet in deutscher Übersetzung:
„Wenn man also nach der Berechnung und dem Konstruieren einer Höhe bemerkt, dass bei dieser Höhe ein gewisser kleiner Fehler [wie Ho – He] begangen wurde, korrigiert man die resultierende Höhe, mit einer Parallelen zu der bereits gezeichneten Linie [Positionslinie] in einer Entfernung in Meilen, die dem erwarteten Fehler in Minuten entspricht, in Richtung des Himmelskörpers [Azimut, Z] oder in die entgegengesetzte Richtung, je nachdem, ob die verwendete Höhe zu klein oder zu groß war.“
Diese Korrekturidee war nicht neu und konnte in den meisten Navigationslehrbüchern der damaligen Zeit im Zusammenhang mit der Erörterung der Sumner Methode gefunden werden. Hilaires Beitrag bestand darin, zu erkennen, dass dieselbe Korrekturidee auch auf die Differenz zwischen der vom Schiffsort aus beobachteten Höhe eines Himmelskörpers und der Höhe von einer angenommenen naheliegenden Position aus angewendet werden kann, um die wahre Standlinie zu bestimmen. Es dauerte dann aber noch knapp zwei Jahre, bis Hilaire seine Methode veröffentlichte. In seiner zweiten Publikation beschreibt Hilaire seine Methode genau. Am Ende seiner Ausführungen fasst er den Kern seiner Überlegungen in wenigen, kurzen Sätzen zusammen. Die deutsche Übersetzung lautet:
„ Zusammengefasst gilt: Zum Berechnen einer Beobachtung berechne die Höhe [He] und das Azimut [Z] des Sterns für die DR-Position [e] und den Beobachtungszeitpunkt. Subtrahiere die berechnete Höhe von der beobachteten Höhe [Ho – He]. Betrachte diese Differenz als einen Versatz des Schiffes. Dabei ist der Kurs durch das Azimut gegeben und die Distanz durch die Höhendifferenz. Korrigiere die Position [e’] entlang dieser Route.“
Zuerst wird also die Sonne beobachtet und die beobachtete Höhe hm sowie die sekundengenaue Zeit der Beobachtung werden festgestellt und festgehalten. Im Weiteren muss die Position eines Gissortes bestimmt werden. Hilaire hat dafür die DR-Position, also den Koppelort als Gissort benutzt. Für diesen Gissort werden jetzt die Höhe zum Beobachtungszeitpunkt und das Azimut berechnet. Dazu sind zwei Formeln nötig, die wohl als die wichtigsten und am häufigsten gebrauchten in der Navigationsgeschichte der vergangenen 150 Jahre gelten. Die Formeln lauten:
![]()
![]()
Um die Formeln anwenden zu können, müssen die Deklination δ und die Variable t bekannt sein. Diese Variable, sie ist auch als LHA (Local Hour Angle) bekannt, bezeichnet einen Ortsstundenwinkel, in diesem Fall den des Gissortes. Der LHA ist die Meridiandistanz eines benannten Ortes bis zum augenblicklichen Bildpunkt der Sonne, und zwar immer nach Westen zählend. Somit ist der Greenwichwinkel Grt der LHA des Ortes Greenwich. Der LHA wird als Summe von Greenwichwinkel Grt und dem geografischen Längengrad des zu betrachtenden Ortes berechnet, also LHA = t = λ + Grt (Westgrade sind negativ).
Beide Werte, die Deklination δ und der Greenwichwinkel Grt müssen einem nautischen Jahrbuch entnommen werden, und zwar für die Sekunde, die sich der Navigator notiert hatte, in welcher er die Sonne im Fernrohr des Sextanten auf die Kimm setzte. Da jetzt alle Werte bekannt sind, kann mit der ersten Formel die Höhe hc berechnet werden. Das Ergebnis gibt an, wie hoch die Sonne in der Sekunde der Beobachtung am Gissort gestanden hatte. Der Index c besagt dabei, dass es eine berechnete (c = calculated) Höhe ist. Die Messung auf dem Schiff lieferte für dieselbe Sekunde die beobachtete Höhe hm. Aus den beiden Höhen wird nun ihre Differenz Δh = hm – hc berechnet. Diese Höhendifferenz wird im englischen als Intercept bezeichnet und auch die Methode ist als Intercept Methode bekannt geworden.
Da nun alles Erforderliche vorliegt, kann mit der Konstruktion der Standlinie, entweder direkt auf der Seekarte oder auf vorbereiteten Leerkarten erfolgen. In Leerkarten sind die Meridianabstände den Abständen der Breitenkreise so angepasst, dass Winkel mit einem normalen Winkelmesser ohne Umrechnung direkt eingezeichnet werden können. Die Konstruktion einer Standlinie verdeutlicht Bild 2.
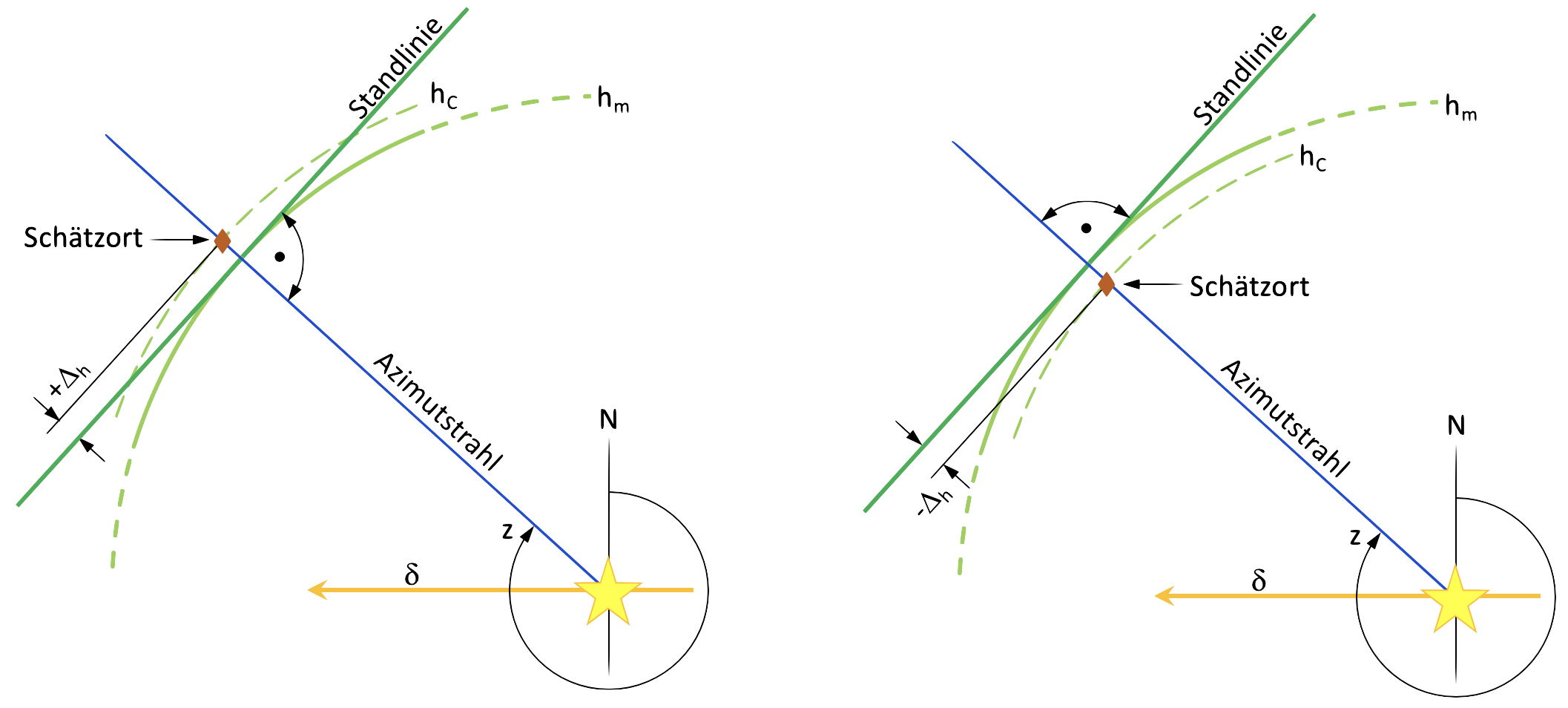
Begonnen wird die Konstruktion z. B. mit einem kleinen Kreuz, das die Position des Gissortes markiert. Durch diese Markierung wird jetzt eine Linie im Winkel des ausgerechneten Azimuts gezogen. Das ist der Azimutstrahl Az. Als Nächstes wird die Differenz Δh, die in Bogenminuten vorliegt als Distanz in Seemeilen vom Gissort ausgehend auf dem Azimutstrahl abgetragen. Das Vorzeichen dieser Differenz , dem Intercept, ist jetzt sehr wichtig. Ist es positiv, dann erfolgt die Abtragung, in Richtung Sonne. Das Schiff war dann während der Beobachtung näher an der Sonne, als der Gissort. Man musste den Blick quasi höher richten. Ist die Differenz negativ, dann wird das Intercept vom Gissort und von der Sonne weg auf dem Azimutstrahl abgetragen. An der Stelle, an der eine Abtragung endet, wird die Standlinie senkrecht zum Azimutstrahl eingezeichnet.
Das Bild ist eine sehr verzerrte Darstellung, in der sogar der Bildpunkt der tausende Meilen entfernten Sonne eingezeichnet ist. Der Gissort als neuer Bezugspunkt schafft nämlich den Vorteil, dass Konstruktionen in seinem Nahfeld möglich sind. Das ist bei zeichnerischen Lösungen wichtig. Der Kreuzungspunkt mit einer zweiten, einige Stunden später beobachteten Standlinie liefert den Standort.
Beispielrechnung
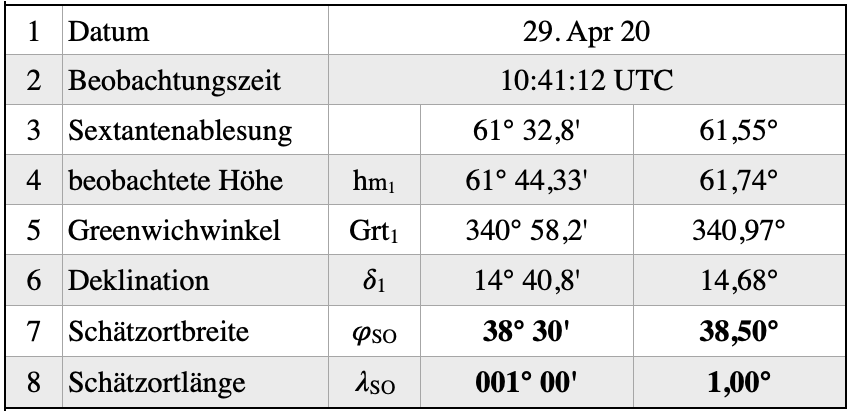
Die Anwendung der Methode lässt sich am besten an Hand eines Beispiels zeigen. Bei einer Fahrt im westlichen Mittelmeer am 29. April 2020 wurde um 10:41:12 UTC die Sonne beobachtet. Auf dem Sextanten wird dabei eine Höhe von 61° 32,8′ abgelesen. Nach einer Korrektur dieses Wertes, der sogenannten Sextantenbeschickung, die mittels der in einem Nautischen Jahrbuch angegebenen Gesamt- und Zusatz Beschickungstabellen erfolgt und einer Berücksichtigung des Indexfehlers wird eine beobachtete Höhe von hm1 = 61° 44,33′ = 61,74° ermittelt.
Als nächstes muss ein Gisort festgelegt werden. In den ersten Jahrzehnten nach Bekanntwerden der Hilaire Methode wurde dafür immer der Koppelort verwendet. Später ging man dazu über, möglichst ganzgradige Kreuzungen von Längen- und Breitengraden zu wählen. Hier definieren wir einfach einen uns bekannten Ort in der Nähe mit den Koordinaten 38° 30’ N 001° 00’ E.
Für die Beobachtungszeit wird jetzt die Position des Bildpunktes der Sonne, aus dem Greenwicher Stundenwinkel Grt und der Deklination ∂ aus dem Nautischen Jahrbuch herausgelesen. Dazu müssen wir die auf der entsprechenden Datumsseite des Jahrbuches gefundenen Stundenwerte mit den Zuschlagwerten für die Sekunden und Minuten, dem sog. Zuwachs addieren. Die Zuwachswerte finden sich in den Schalttafeln im hinteren Teil des Buches. Für die Deklination reicht eine minutengenaue Angabe aus. Wir fassen alles in folgender Tabelle zusammen:
Mit der Bildpunktposition, dem Koppelort und dem Nordpol haben wir jetzt ein genau definiertes nautisches Dreieck, auf der Erdoberfläche, an dem wir die notwendigen Berechnungen durchführen können.
Standlinie 1 nach erster Beobachtung
Zu berechnen sind zunächst Höhe und Azimut des Schätzortes zum Beobachtungszeitpunkt. Wie das geht, wird am Ende des Beitrags die Sonne am Himmel gezeigt, so dass hier nur noch die Gleichungen angegeben werden. Mit ![]() SO und
SO und ![]() SO, der Position des Schätzortes, errechnen wir die Höhe der Sonne, wie sie ein Beobachter zur selben Beobachtungszeit von dort aus aus sehen würde. Die dazu benutzte Gleichung lautet:
SO, der Position des Schätzortes, errechnen wir die Höhe der Sonne, wie sie ein Beobachter zur selben Beobachtungszeit von dort aus aus sehen würde. Die dazu benutzte Gleichung lautet:
(1) ![]()
Hierin ist t der Ortsstundenwinkel (auch LHA = Local Hour Angel). Es ist ein Stundenwinkel wie der Greenwich Stundenwinkel Grt aus dem nautischen Jahrbuch. Der Unterschied besteht nur darin, dass er nicht vom Ort Greenwich aus zählt. Er zählt von einem benannten Ort aus, hier ist es der Schätzort und er zählt ebenfalls in westliche Richtung bis zum Meridian des Bildpunktes der Sonne. Dieser Ortsstundenwinkel wird dadurch berechnet, dass Grt und Schätzortlänge vorzeichenrichtig addiert werden. Westlängen sind bekanntlich negativ. Ist das Ergebnis größer als 360° dann werden 360° subtrahiert. Ist das Ergebnis negativ, dann werden 360° addiert. Bei Benutzung in einer Kosinusfunktion wie in der vorstehenden Gleichung können die Operationen mit den 360° weggelassen werden. Die Kosinusfunktion ist symmetrisch und periodisch und hat alle 360° sowieso immer wieder denselben Wert. Wenn wir alle bis jetzt vorhandenen Werte einsetzen, dann erhalten wir als Höhe für den Koppelort 61° 21,55’. Daraus ergibt sich jetzt die Differenz zwischen der vom Schiff aus beobachteten Höhe hm und der für den Schätzort berechneten Höhe hc. Wir erhalten:
(2) ![]()
Als nächstes brauchen wir das Azimut z der ersten Beobachtung und das bekommen wir am einfachsten aus:
(3) ![]()
Das Azimut ist gleich einem Kurs auf den Bildpunkt der Sonne und somit als rechtsdrehender Winkel gegenüber dem nach Norden weisenden Teil des Schätzort Meridians. Am Schiffsmittag passiert die Sonne diesen Meridian des Schätzortes im Süden und das Azimut beträgt dann logischerweise 180°. Die Sonne wandert weiter in Richtung Westen und das Azimut steigt dabei bis auf 360° an. Am Schiffsmittag ist der Ortsstundenwinkel t gleich null, weil Standortmeridian und Bildpunktmeridian identisch sind.
Der Arcus Kosinus in der Gl. 3 kann nur Ergebnisse liefern, die zwischen 0° und 180° bzw. 0 und ![]() liegen. Damit wird t bis zum Schiffsmittag von Gl. 3 richtig berechnet. Vom Schiffsmittang an liefert Gl. 3 für die darauffolgenden 12 Stunden Winkel, die von 180° bzw.
liegen. Damit wird t bis zum Schiffsmittag von Gl. 3 richtig berechnet. Vom Schiffsmittang an liefert Gl. 3 für die darauffolgenden 12 Stunden Winkel, die von 180° bzw. ![]() ausgehend bis auf null abnehmen. Da das Azimut jedoch weiter bis auf 360° zunimmt, ergibt sich die folgende Rechenregel zur Bestimmung des Azimuts:
ausgehend bis auf null abnehmen. Da das Azimut jedoch weiter bis auf 360° zunimmt, ergibt sich die folgende Rechenregel zur Bestimmung des Azimuts:
- z{t > 180°} = z* (vormittags)
- z{t < 180°} = 360° – z* (nachmittags)
Das Zeitazimut
Anstelle dieses sogenannten Höhenazimuts, weil zu seiner Berechnung die beobachtete Höhe benutzt wird, kommt bei Benutzung dieser Methode oft auch das sogenannte Zeitazimut zur Anwendung. Die Gründe dafür sind nicht unbedingt nachvollziehbar. Warum sollte eine kleine Ungenauigkeit des Höhenazimuts gegenüber dem Zeitazimut eine Rolle spielen, wenn allein die Schätzung des Koppelortes schon das größte Fehlerpotential in sich birgt. Außerdem machen Berechnungsfehler sowieso nur einen vernachlässigbar geringen Anteil in der Standortgenauigkeit aus.
Wir wollen dieses Zeitazimut in diesem Beispiel auch nicht weiter bevorzugen, obwohl es vielfach zum Standard bei Hilaire zählte. Die einzelnen Schritte der Herleitung der Formel für das Zeitazimut sollen auch nicht angegeben werden, nur die Formel selbst und auch die nur zur Information. Sie lautet:
(4) ![]()
Da die Arkustangens Funktion nur Werte zwischen 0° und 90° liefern kann, sind hier gleich vier Bedingungen zu beachten, um ein vollkreisiges Azimut zu erhalten. Allgemein gilt dann:
(5) ![]()
und
(6) ![]()
Konstruktion der ersten Standlinie
Das Azimut, ganz gleich nach welcher Methode es berechnet wurde und die ermittelte Höhendifferenz ermöglichen jetzt die Konstruktion der Standlinie aus der ersten Beobachtung. Die folgende Tabelle fasst die ermittelten Werte noch einmal zusammen.
Die Konstruktion der Standlinie erfolgt entweder direkt auf der Seekarte oder auf einer sogenannten Leerkarte. Bild 3 zeigt das Ergebnis für die erste Standlinie. Man beginnt mit der Markierung des Schätzortes als kleines Kreuz oder Punkt. Hier ist es ein kleiner mit SO bezeichneter Kreis. Die Koordinaten dazu stehen in der ersten Tabelle, die etwas weiter oben gezeigt wurde. Durch diesen Schätzort wird jetzt der Azimutstrahl im Winkel des Azimuts von 141,35° gezogen.

Ist das erfolgt, dann wird das ausgerechnete Intercept von -22,78’ auf den Zirkel genommen und vom Schätzort ausgehend in Richtung des Bildpunktes auf dem Azimutstrahl abgetragen. Den Zirkelradius stellen wir an einem Lineal ein. Wenn der Massstab 2 mm pro Winkelminute ist, dann nehmen wir eine Zirkelspanne von 45,5 mm auf. Das negative Intercept verkürzt die Azimutlinie zwischen Bildpunkt und Schätzort. Am Ende der abgetragenen Strecke wird eine Gerade senkrecht durch den Azimutstrahl gezeichnet. Diese Gerade ist die Standlinie SL1.
Um Schätzort, Azimutstrahl, Höhendifferenz und Standlinie einzeichnen zu können, eignen sich Leerkarten am besten. Die müssen extra für die jeweilige Breite, auf der man segelt, angefertigt werden. Darauf sind dann Abstände zwischen den Längengraden in der richtigen Weise festgelegt und man kann die Längenachse auch beschriften. In diesem Beispiel befindet sich unser Gebiet auf 38° nördlicher Breite. Die Entfernung zwischen zwei ganzgradigen Längen beträgt dort nur 0,788 mal der Entfernung zwischen zwei ganzgradigen Breiten. Die Zahl 0,788 ist der Kosinus von 38°.
Es geht aber auch mit Millimeterpapier. Wird das benutzt, dann darf die horizontale Längenachse nicht beschriftet werden. In den Bildern 3 bis 5 werden Leerkarten benutzt, die man sich leicht selbst herstellen kann. In den Bildern 3 bis 5 beträgt der Abstand zwischen den horizontzalen Linien 10′ bzw. 10 NM.
Versegelung
Zwischen den Beobachtungen findet normalerweise eine Ortsveränderung statt. Der Standort wird „versegelt“ und weil man überhaupt nicht weiß, welcher Punkt auf der Standlinie 1 letztlich der Standort ist, muss die gesamte Standlinie versegelt werden. Versegelungen werden zu genau dem Zeitpunkt einer zweiten Beobachtung berücksichtigt. Im Beispiel soll eine Koppelnavigation (Dead Reckoning) in der Zeit zwischen den Beobachtungen eine mittlere Distanz von d = 19 NM auf einem mittleren Kurs von c = 23° ergeben haben.
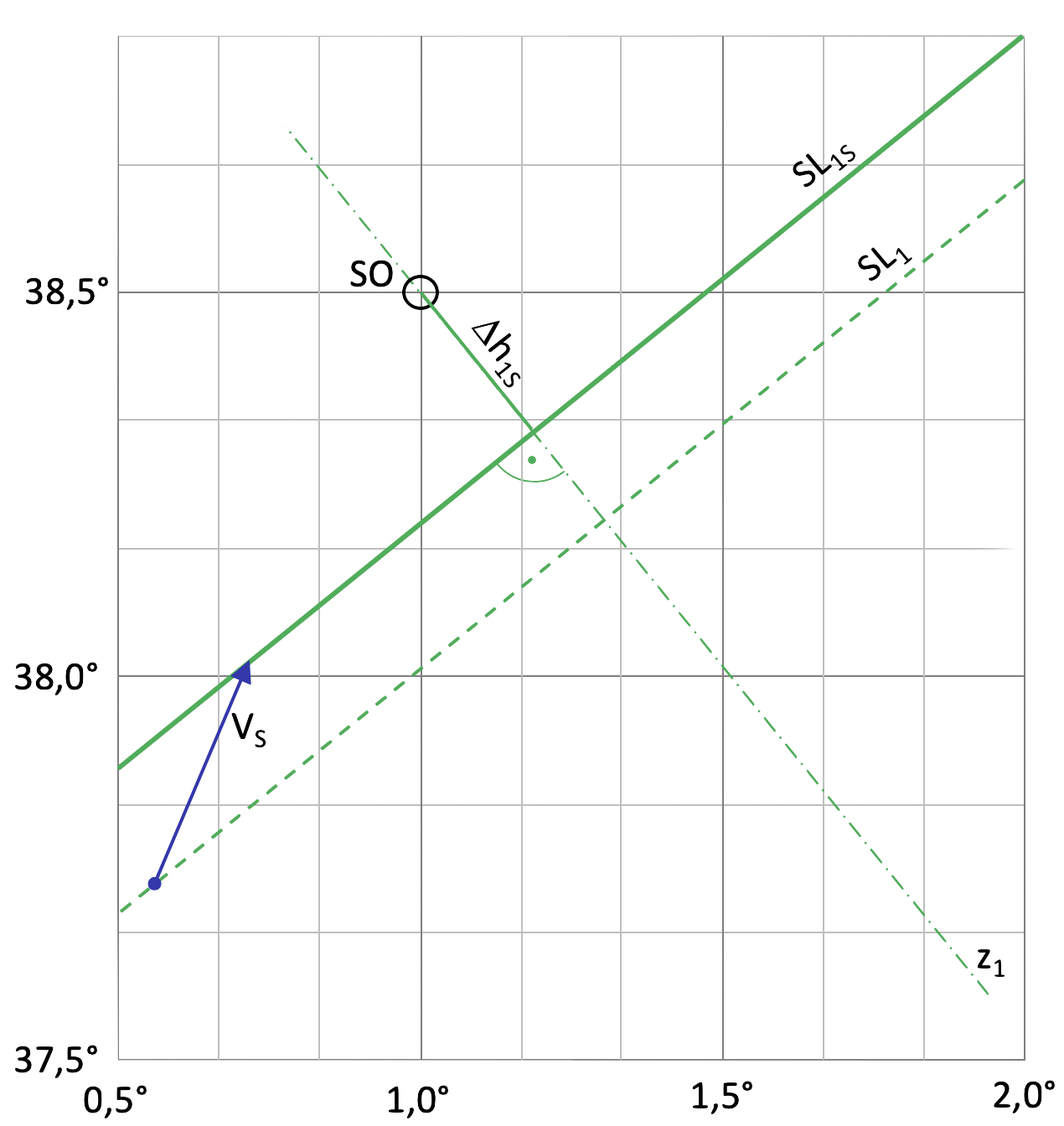
Daraus kann jetzt ein Versegelungsvektor gebildet werden. Das ist der blaue mit VS bezeichnete Pfeil im Bild 4. Dieser Pfeil startet an einem beliebigen Punkt der Standlinie 1. Anschließend wird die Standlinie 1 so weit parallel verschoben, dass sie durch die Pfeilspitze verläuft. Das Ergebnis ist die versegelte Standlinie 1. Die ursprüngliche Standlinie aus der ersten Beobachtung ist im Bild noch gestrichelt dargestellt.
Es geht aber auch einfacher, indem die Versegelung über eine Höhenanpassung berücksichtigt wird. Diese Berechnungsart ist zudem noch etwas präziser. Doch das nur mathematisch, was praktisch überhaupt nicht ins Gewicht fällt. Der größte Fehler in der Berücksichtigung von Versegelungen kommt durch eine ungenaue Kopplung zustande. Die Höhenänderung kann ganz einfach mit Hilfe einer Formel nach Douwes ausgerechnet werden, die in Verbindung mit der Gauß Methode ebenfalls angewendet wurde. Diese Formel für eine Höhenkorrektur hK lautet in der Anwendung mit den Zahlen:
![]()
![]()
Damit die Masseinheiten einheitlich Grad sind, wurde die versegelte Distanz d von nautischen Meilen in Grad umgerechnet, indem sie durch 60 dividiert wird. Das Ganze auszurechnen dauert nur ein paar Sekunden. Gebraucht wird dazu das Azimut aus der ersten Beobachtung, das bereits vorliegt. Die ausgerechnete Höhenkorrektur hK durch Versegelung in diesem Beispiel ist negativ. Man muss diese Korrektur von der Höhendifferenz ![]() abziehen und erhält die korrigierte Höhendifferenz
abziehen und erhält die korrigierte Höhendifferenz ![]() :
:
(7) ![]()
Wenn wir nach dieser rechnerischen Variante vorgehen, dann zeichnen wir die Standlinie im Bild 3 gleich mit der versegelten Höhendifferenz ![]() . Die Parallelverschiebung, wie sie im Bild 4 gezeigt wird entfällt und wir können sofort mit dem Zeichnen der Standlinie aus der zweiten Beobachtung fortfahren.
. Die Parallelverschiebung, wie sie im Bild 4 gezeigt wird entfällt und wir können sofort mit dem Zeichnen der Standlinie aus der zweiten Beobachtung fortfahren.
Standlinie 2 nach zweiter Beobachtung
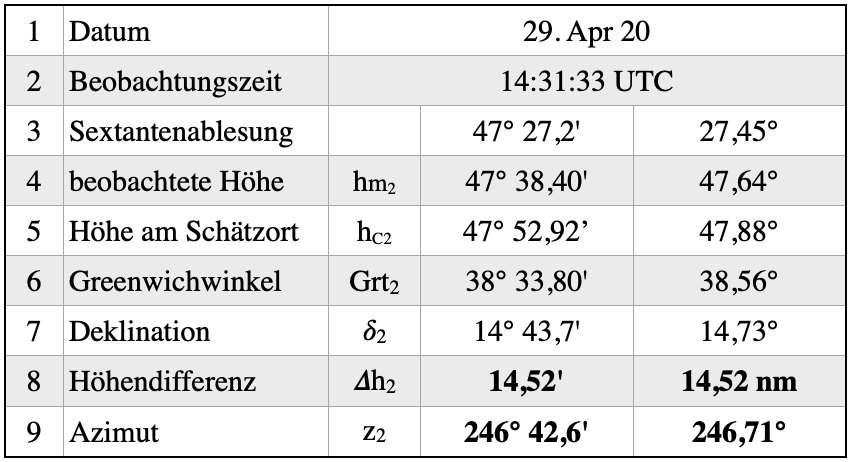
Die erste Standlinie ist versegelt und die Daten aus der zweiten Beobachtung liegen vor. Die zweite Beobachtung der Sonne erfolgte am gleichen Tag um 14:31:33 UTC. Am Sextant wurde dabei ein Winkel von 47° 27,23′ abgelesen, der zu berichtigen ist. Wir erhalten eine beobachtete Höhe von 47° 38,40′ bzw. 47,64° als Dezimalwert.
Für Datum und Uhrzeit der Beobachtung liefert das Nautische Jahrbuch Deklination und Greenwichwinkel. Aus Grt2 und der Schätzortlänge wird der Ortsstundenwinkel t2 berechnet. Dazu werden wie üblich Grt2 und Schätzortlänge addiert. Weil t in einer Kosinusfunktion verwendet wird, kann man sich die Beseitigung von Überträgen durch Addition oder Subtraktion mit 360° wieder schenken. Die für den Schätzort berechnete Höhe bekommen wir mit folgender Gleichung:
(8) ![]()
Nach Einsetzen der Zahlen berechnet sich die Höhe am Schätzort mit 47° 52,92’. Damit kann jetzt auch die zweite Höhendifferenz ![]() berechnet werden und wir erhalten:
berechnet werden und wir erhalten:
(9) ![]()
Das Azimut wird auch hier als Höhenazimut bestimmt:
(10) ![]()
Nach Einsetzen aller Werte erhälten wir das berechnete Azimut z* mit 113,29°. Da die Messung am Schiffsnachmittag stattgefunden hat, die Sonne hat den Standort bereits überholt und die Richtung der Beobachtung war damit die westliche Hemisphäre, muss dieser errechnete Wert von 360° abgezogen werden und wir erhalten ein Azimut von z2 = 246,71°. In der nachstehenden Tabelle sind die Daten zusammengefasst:
Damit kann jetzt die Zeichnung vervollständigt werden. Zuerst wird wieder rechtweisend Nord, durch den markierten Schätzort hindurch, der Azimutstrahl im Winkel von 246,7°, eingezeichnet. Danach werden 29 mm auf den Zirkel genommen, was 14,52 NM entspricht. Diese positive Höhendifferenz ![]() führt zu einer Verlängerung des Azimutstrahls über den Schätzort hinaus. Sie wird vom Schätzort ausgehend und vom Bildpunkt wegführend abgetragen. An der mit der Zirkelspanne markierten Stelle wird nun im rechten Winkel zum Azimutstrahl die zweite Standlinie SL2eingezeichnet. Beide Standlinien, SL1V und SL2, schneiden sich jetzt im Standort, an der Position P.
führt zu einer Verlängerung des Azimutstrahls über den Schätzort hinaus. Sie wird vom Schätzort ausgehend und vom Bildpunkt wegführend abgetragen. An der mit der Zirkelspanne markierten Stelle wird nun im rechten Winkel zum Azimutstrahl die zweite Standlinie SL2eingezeichnet. Beide Standlinien, SL1V und SL2, schneiden sich jetzt im Standort, an der Position P.
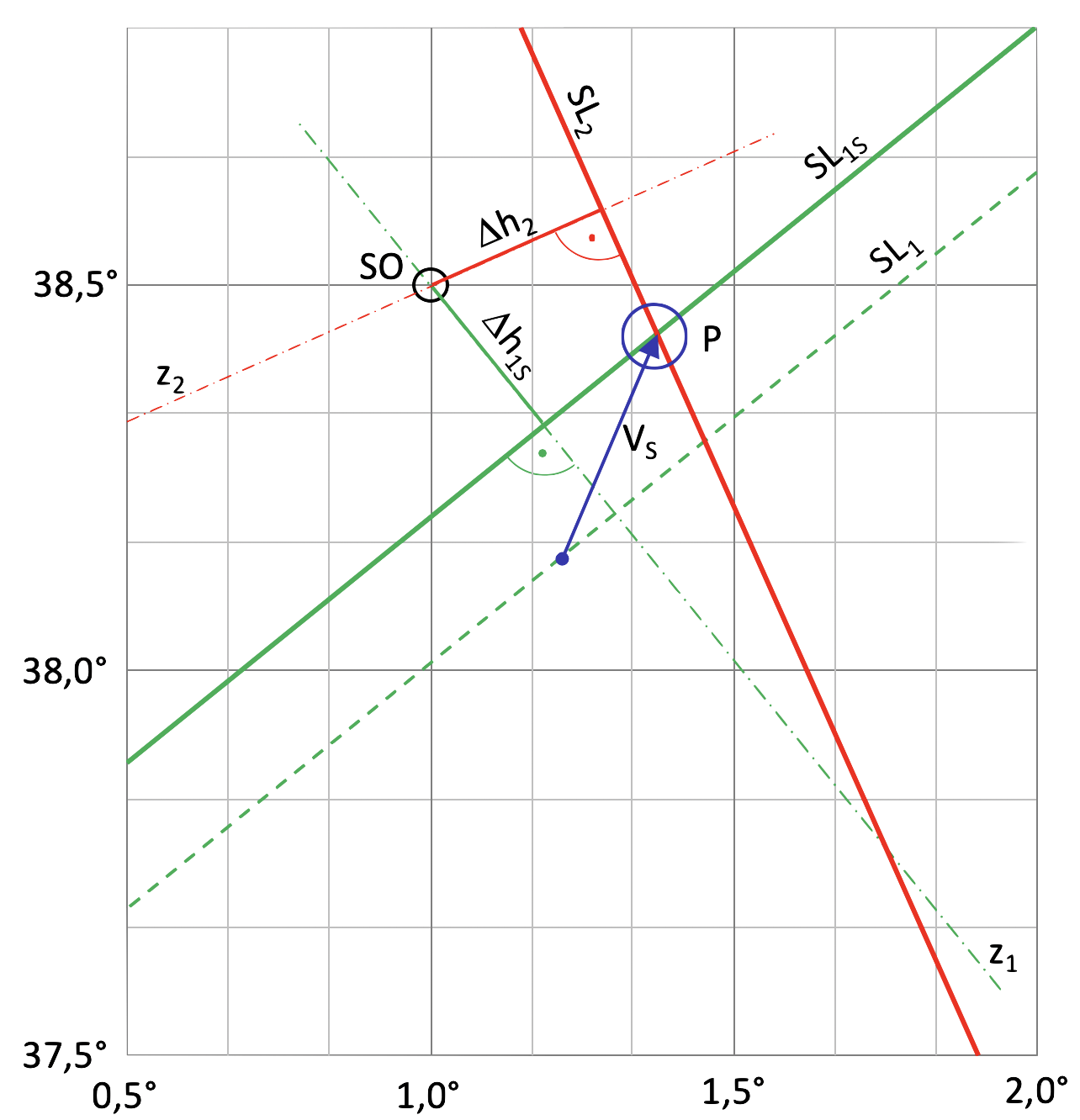
Die Methode nach Hilaire ist eine grafische Methode und der Standort muss aus der Zeichnung herausgelesen bzw. herausgemessen werden. Es kommt also darauf an, dass sehr präzise und mit dünnen Linien gezeichnet wird. Zum Herausmessen werden Abschnitte zu ganzgradigen oder nächstgelegenen Gitterlinien gewählt.
Mit dem Zirkel messen wir auf der Karte, dass der Standort 52,5 mm nördlich der Breite von 38° N liegt. Diese Entfernung multiplizieren wir mit dem vertikalen Maßstab von 1’/2 mm und erhalten 26,25′. Die Standortbreite ist damit 38° 26,25′.
Weiter messen wir, dass der Standort auf der Karte 34,8 mm östlich von 1° E liegt. Das Produkt dieser Spanne mit dem horizontalen Maßstab von 1’/1,576 mm liefert 22,08′. Der horizontale Maßstab auf 38° Breite basiert auf dem Kosinus von 38° = 0,788, wenn 10 NM auf der Karte 20 mm sein sollen. Die Standortlänge ist damit 1° 22,08′ E.
Unsere Schiffsposition P lautet also
38° 26,25’ N / 001° 22,08’ E.
Zum Vergleich erhalten wir nach der Gauß Methode einen Standort von
38° 26,40’ N / 001° 22,17’ E
Die Gauß-Methode kann als Referenzmethode gelten, da sie mit der Erde als ideale Kugel genau rechnet. Im Verleich liegt dann der Gauß-Standort 278 m nördlicher und 167 m östlicher. Das ist kein großer Unterschied und beruht nur auf der Rechenmethode. Abweichungen vom wahren Standort sind etwas völlig anderes, weil ihre Ursachen unvermeidbare Fehler bei der Messung von Zeit, Höhe und Vertsegelung sind.
Schlussfolgerung
Das alles und noch viel mehr wird in einem Lehrgang über astronomische Navigation vermittelt. Es ist keine höhere Mathematik, aber ein dickes Paket von Anweisungen und Rechenvorschriften. Die Werkzeugkiste, die zu dem Ganzen gebraucht wird enthält
- einen Sextanten,
- eine Stoppuhr,
- eine Quarzuhr als Chronometer für die UTC,
- ein Nautisches Jahrbuch,
- einen möglichst programmierbaren Taschenrechner,
- Papierseekarten,
- Leerkarten oder Millimeterpapier und
- Zirkel, Lineal, Winkelmesser oder Kursdreieck.
Ohne Übung oder besser Routine kann niemand auf diese Methode zurückgreifen, wenn das mal nötig sein sollte. Als Rückfallmethode für jeden Fahrtensegler, wie das mal angedacht war, ist sie deshalb vollkommen ungeeignet. Auch für den Hobbynavigator, der gern klassisch mit dem Sextanten unterwegs ist, dürfte diese Art der Standortermittlung eine Herausforderung sein. Sie passt einfach nicht mehr in unsere Zeit. Die vielen hundert Euro, die so mancher Leergang auch heute noch kostet, kann man sich sparen. In der Segelliteratur oder im Internet findet man unter dem Begriff Astronavigation auch immer nur diese Methode. Sie scheint ein Synonym für Astronavigation geworden zu sein.
Als Rückfallmethode wird Astronavigation erhalten bleiben, jedoch nur unter der Bedingung, dass Rechnen, Zeichnen und Herumsuchen in Tabellen entfallen und auch keinerlei mathematische oder astronomische Kenntnisse erforderlich sind. Außerdem darf ein derartiges Backup nicht viel kosten. Ob man ein Navigations Backup tatsächlich braucht, darüber kann man streiten. Doch jedem sollte klar sein, dass kein System absolut sicher ist und Ausnahmesituationen nicht unmöglich sind.
Verwendung in einem Navigationsprogramm
Damit jeder in der Lage ist, mit einem Sextanten navigieren zu können, so etwa in einem Notfall, müssen die geeigneten Mittel vorhanden sein. Das vorstehend beschriebene Höhendifferenzverfahren, und ebenso die nachfolgend beschriebene Navigation mit den HO 249 Tafeln sind in diesem Sinne keine geeigneten Mittel. Diese Verfahren sind nur dafür geeignet, traditionsgemäß mit Sonne, Mond, Planeten und Sternen auf Papier zu navigieren, was durchaus ein schönes Hobby ist und alte Seefahrertraditionen am Leben erhält. Für den allgemeinen Gebrauch in der heutigen Zeit sind nur Computer Apps geeignet, die jeder ohne Voraussetzungen sofort anwenden kann.
In den letzten Jahrzehnten wurden immer wieder Computerprogramme oder Apps für Mobilgeräte entwickelt, die das Verfahren von Saint Hilaire zur Grundlage haben. Mit diesem Verfahren hat die weltweite Seefahrt mehr als 100 Jahre lang erfolgreich navigiert und so hat sich in dieser Zeit seine alleinige Kompetenz in der gesellschaftlichen Meinung festsetzen können. Doch Fakt ist, es handelt sich dabei nur um einen Notbehelf aus dem 19. Jahrhundert. Die richtigen Navigationsprogramme gab es schon früher. Sie konnten aber nicht verwendet werden, weil es keine Elektronenrechner gab.
Wer das Hilaire Verfahren digitalisiert, der weiß nicht, dass Saint Hilaire das Sumner Verfahren für eine optimale zeichnerische Verwendung und nicht für eine optimale digitale Verwendung modifiziert hat. In programmierter Form ist das dann nichts weiter als eine Kopie sämtlicher Arbeitsschritte eines Navigators aus früherer Zeit. Das ursprüngliche Sumner Verfahren kann jedoch auch ganz leicht für digitale Anwendungen optimiert werden, und dann entfallen all seine Restriktionen und sogar die Standortschätzung.
Doch auch das wäre Unfug. Es ist doch wahrlich umständlich, den gekrümmten Verlauf der Höhengleichen im Standortbereich, der zu diesem Zweck erst mal geschätzt werden muss, durch Geraden zu ersetzen, und dann den Standort mit diesen Geraden zu finden. Zu guter Letzt ist das Ergebnis dann noch nicht einmal der genaue Standort und Höhen über 80 Grad können sogar zu Fehlern führen. Das alles erinnert an den Spruch, mit der Hose und der Kneifzange.
Navigieren mit Tafeln
Nicht zuletzt durch die aufkommende Fliegerei entstand die Notwendigkeit, den Rechenaufwand mit den umständlichen Logarithmen und damit die Rechenzeit zu reduzieren. So entstanden verschiedene Tafelwerke. Eine größere Bedeutung bekamen dabei die vom U.S. Hydrographic Office bzw. von deren Nachfolgeorganisation, dem Naval Oceanographic Office herausgegebenen Tafelwerke Pub. No. 229 für die Marine und Pub. No. 249 für die Luftfahrt. Früher bezeichnete man die Tafeln auch als HO 229 bzw. HO229.

Während die Marine Tafeln vorwiegend von der Marine und der Großschifffahrt benutzt wurden, waren die HO 249 Tafeln insbesondere bei Seglern beliebt und werden sogar heute noch verwendet. Der erste Band umfasst ausgewählte Fixsterne mit einer Deklination bis 80° und war immer nur 5 Jahre gültig, weil die Position der Fixsterne gar nicht so fix ist. Der zweite Band umfasst die geographischen Breiten 0°-40° und eine Deklination bis 29°. Der dritte Band umfasst die geographischen Breiten 39°-85° und deckt eine Deklination bis 29° ab. Band 2 und 3 sollen ewige Gültigkeit besitzen. Nachdem die Bände vorübergehend nicht mehr verlegt wurden und Band 1 auch ungültig geworden war, sind nun alle drei Bände wieder als gebundene Bücher erhältlich. Zur Navigation wird außerdem das Nautische Jahrbuch benötigt. Die Bücher können außerdem als PDF Dateien aus dem Netz heruntergeladen werden.
Die Tafelmethode ist die einzige, die ohne elektronische Hilfmittel mit vertretbarem Aufwand zu einem Ergebnis führt. Nachfolgend wird nur eine kurze Einführung gegeben, um das Prinzip aufzuzeigen. Wer sich entschließt tiefer einzusteigen der kann sich in der zahlreich dazu vorhandenen Literatur informieren. Verständlich geschrieben ist ein Buch von Bobby Schenk mit dem Titel „Astronavigation ohne Formeln-praxisnah„.
Grundlage des Navigierens mit Tafeln ist die Methode von Hilaire. Dreh- und Angelpunkt dieser Methode sind bekanntlich Höhe und Azimut eines nahegelegenen Schätzortes. Sind diese beiden Größen berechnet, kann eine Standlinie auf dem Papier gezeichnet werden. Zwei Standlinien, die sich kreuzen, liefern mit ihrem Kreuzungspunkt den Standort und so braucht es mindestens zwei Beobachtungen für einen Standort. Die Tafelmethode ersetzt hierbei nur das lästige Berechnen von Höhe und Azimut, indem diese Größen nun aus einer Zahlentabelle hersausgelesen werden.
Bevor überhaupt mit den Sight Reduction Tafeln gearbeitet werden kann, müssen Greenwichwinkel und Deklination eines Beobachtungszeitpunktes aus einem Nautischen Jahrbuch ermittelt werden. Zur Vorbereitung gehören ebenfalls die Bestimmung der ganzgradigen Breite eines sogenannten Rechenortes, die aus dem Koppelort abgeleitet wird und die Ermittlung eines ganzgradigen Ortsstundenwinkels eines Rechenortes. Aus diesen Werten liefern die Tabellen direkt die tabellierte Höhe Hc, eine Differenz d und das Azimut Z. Die Höhe Hc muss anschließend noch mit Hilfe einer zusätzlichen Tabelle interpoliert werden. Das Azimut Z muss nur nach den auf jeder Seite angegebenen Regeln entsprechend dem gegebenen Ortsstundenwinkel korrigiert werden. Diese Korrektur ist nötig, weil das Azimut auch in der Tafel nur bis 180° berechnet ist. Das alles ist zwar ziemlich komplex und ohne Routine nicht einfach zu bewältigen. Doch alle diese Tätigkeiten sind allein mit Sucharbeiten in den Tabellenbüchern und sonst nur mit Additionen und Subtraktionen zu bewältigen.
Wenn am Ende die Daten von Rechenortbreite, Rechenortlänge, Azimut und Höhendifferenz vorliegen, kann die Standlinie entweder direkt auf der Seekarte oder auf einer extra für die Rechenortbreite angefertigten Leerkarte konstruiert werden. Die Kreuzung dieser ersten mit einer zweiten Standlinie auf der Basis einer weiteren Beobachtung, die einige Zeit später erfolgt, liefert einen grafischen Standort. Dieser wird dann aus der fertigen Zeichnung unter Beachtung des gewählten Maßstabs herausgelesen.
Beispiel
Im folgenden wird gezeigt, wie ein Standort aus zwei Höhen nach der Tafelmethode ermittelt wird. An Werkzeugen werden gebraucht: Band 3 der HO 249, das Nautische Jahrbuch von 2019, ein Taschenrechner oder gutes Kopfrechnen und Zeichenmaterial. Für die Breite des Koppelortes werden Leerkarten benötigt, die im voraus angefertigt werden sollten. Durch den Gebrauch von Leerkarten werden die Original Seekarten geschont. Zur Beobachtung der Sonne werden ein Sextant und eine Stoppuhr benötigt. Die Stoppuhr ist ein praktisches Hilfsmittel und wird unmittelbar vor Beginn der Beobachtung zu einer vollen Minute eines in UTC geeichten Chronometers gestartet. Der Navigator kann so die Sonne ungestört mit dem Sextanten beobachten. Sobald er diese optimal auf den Horizont setzen konnte, ruft er z. B. „stopp“ und ein Helfer hält die Stoppuhr an. Die Stoppuhrzeit addiert mit der Startzeit der Stoppuhr ergeben so die Beobachtungszeit.
Am 29. April 2019 vormittags um um 9:55:51 UTC auf dem Mittelmeer setzt der Navigator den Unterrand der Sonne im Teleskop des Sextanten auf den Horizont. Am Gradbogen und der Trommel des Sextanten wird daraufhin ein Kimmabstand von 56° 29,6′ abgelesen. Nach einer Korrektur dieses Winkels entsprechend dem im April herrschenden Durchmesser der Sonnenscheibe, der Augeshöhe, der Refraktion und dem Indexfehler des Instruments ergab sich daraus eine beobachtete Höhe von 56° 23,9′. Als Koppelposition wurde einfach eine am Vortag festgestellte Position gewählt. Diese Position war mit 38°46,50′ N und 004°47,00′ E angegeben. Die folgende Aufstellung zeigt alle diese Daten als Übersicht.
- Datum 29. April 2019
- Beobachtungszeit 9:55:51 UTC
- Sextantenablesung 56° 29,6′
- beobachtete Höhe 56° 41,02′
- Koppelortbreite 38° 46,50 N
- Koppelortlänge 004° 47,00′ E
Die erste Standlinie
Die nächste Aufgabe des Navigators ist es nun, aus diesen Angaben den Greenwichwinkel Grt und die Deklination δ, wie sie zum Beobachtungszeitpunkt herrschten, aus einem Nautischen Jahrbuch herauszulesen. Dazu findet er auf der Tagesseite die Winkel im Stundenraster und notiert sie. Anschließend sucht er die Zuwächse für 55 min und 51 s, die in der Schalttafel auf einer der letzten Seiten des Buches gefunden werden. Die Zuwächse werden jeweils addiert und die Summen liefern die Koordinaten des Bildpunktes der Sonne. Für den Greenwichwinkel wird gerechnet:
- Grt um 9:00 UT1 315° 38,7′
- Zuwachs für 55m 51s: 13° 57,8′
- Grt um 9:55:51 UT1: 329° 36,5′
Im Gegensatz zum Grt ändert sich die Deklination nicht linear, sondern vielmehr etwa sinusförmig. Steng genommen sollte die Änderung der Deklination δ innerhalb einer Stunde deshalb nicht mit einem Dreisatz ausgerechnet werden. So wird sie sich im Frühjahr in einer ersten Halbstunde schneller ändern, als in der folgenden zweiten Halbstunde, weil die Deklination zu den Sonnenwenden zunehmend bis auf null abflacht. Aus diesem Grunde gibt es in der Schalttafel die Spalten Unt (Unterschied) und Vb (Verbesserung). Dabei gibt Unt den stündlichen Wert der Deklinationsänderung, sozusagen das Differential an. Sein Wert schwankt im Laufe eines Jahres zwischen 0′ und 1′.
Leider enthält die Unt-Spalte in der Schalttafel nur Werte im 0,3′ Raster und nicht im 0,1′ Raster wie auf den Tagesseiten, so dass man über den Daumen peilen müsste. Das könnte allerdings zu Falschinterpretationen führen. Vb sollte deshalb besser als Produkt von Unt und dem Dezimalwert der angebrochen Minuten ausgerechnet werden. In diesem Beispiel ist Unt auf der Tagesseite mit 0,8′ angegeben. Der Dezimalwert der angebrochenen Stunde errechnet sich mit 55/60 = 0,92 und damit beträgt die Verbesserung 0,8′ · 0,92 = 0,73′. Jetzt ist nur noch zu überlegen, ob Vb addiert oder subtrahiert wird. Für das Datum der Beobachtung nimmt die Deklination zu und deshalb wird der Navigator Vb addieren und mit N wie Nord bezeichnen.
- δ um 9:00 UT1: 14° 25,3′ N
- Vb: 0,7′ N
- Deklination δ 14° 26,0′ N
Leider ist es nicht möglich, im Abstand von Zehntelminuten alle möglichen Koppelorte auf der Welt in einer Tabelle unterzubringen. Der Umfang wäre riesig und so ist man auf ganzgradige Größen ausgewichen. Die Präzision ist dann zwar nicht übermäßig aber immehin gut. Gegenüber der original Hilaire Methode werden dadurch einige Begriffe auf die Verwendung mit den Tafeln angepasst.
- Koppelortbreite
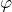 : Bei einem Koppelort handelt es sich um eine bloße Vermutung. Damit ist auch die dafür ermittelte Breite
: Bei einem Koppelort handelt es sich um eine bloße Vermutung. Damit ist auch die dafür ermittelte Breite 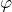 nur eine Annahme der tatsächlichen Schiffsbreite. Der geschätzte Wert wird deshalb auf den nächstgrößeren oder nächstkleineren ganzzahligen Breitengrad gerundet und mit LATbezeichnet.
nur eine Annahme der tatsächlichen Schiffsbreite. Der geschätzte Wert wird deshalb auf den nächstgrößeren oder nächstkleineren ganzzahligen Breitengrad gerundet und mit LATbezeichnet. - Deklination
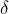 : Die Deklination wird auf den nächsten ganzzahligen Breitengrad gerundet und dann als DECLINATION bezeichnet.
: Die Deklination wird auf den nächsten ganzzahligen Breitengrad gerundet und dann als DECLINATION bezeichnet. - Ortsstundenwinkel t: Der Ortsstundenwinkel Grt +
 (0 < t < 360°) ist ebenfalls nur eine Vermutung. Er wird so abgeändert, dass sich ein ganzgradiger Ortsstundenwinkel ergibt. Dieser wird dann mit LHAbezeichnet. Dabei muss der LHA so gewählt werden, dass er möglicht nahe am ursprünglichen Koppelort liegt.
(0 < t < 360°) ist ebenfalls nur eine Vermutung. Er wird so abgeändert, dass sich ein ganzgradiger Ortsstundenwinkel ergibt. Dieser wird dann mit LHAbezeichnet. Dabei muss der LHA so gewählt werden, dass er möglicht nahe am ursprünglichen Koppelort liegt. - Koppelort KO: Durch die letztendlich nur möglichen ganzgradigen Werte von LAT und LHA wird der ursprüngliche Koppelort obsolet. Er beruht ohnehin nur auf einer Vermutung. An seine Stelle tritt ein Rechenort, von dem aus die Standlinienkonstruktion erfolgen wird.
Die Rechenortbreite LAT ist schnell gefunden, indem die Koppelortbreite ![]() = 38° 46,50′ N auf LAT = 39° N aufgerundet wird. Doch nun folgt die heikelste Stelle der Navigation mit der HO 249. Es muss nämlich eine sogenannte Rechenortlänge gefunden werden, die mit dem Grt einen optimalen ganzzahligen LHA ergibt. Das geht in drei Schritten. Zuerst wird der Stundenwinkel t des Koppelortes ausgerechnet. Bekanntlich wird dazu vorzeichenrichtig die Koppelortlänge mit dem Greenwichwinkel addiert. Eventuelle Überträge müssen danach durch Addition oder Subtraktion von 360° beseitigt werden:
= 38° 46,50′ N auf LAT = 39° N aufgerundet wird. Doch nun folgt die heikelste Stelle der Navigation mit der HO 249. Es muss nämlich eine sogenannte Rechenortlänge gefunden werden, die mit dem Grt einen optimalen ganzzahligen LHA ergibt. Das geht in drei Schritten. Zuerst wird der Stundenwinkel t des Koppelortes ausgerechnet. Bekanntlich wird dazu vorzeichenrichtig die Koppelortlänge mit dem Greenwichwinkel addiert. Eventuelle Überträge müssen danach durch Addition oder Subtraktion von 360° beseitigt werden:
(11) ![]()
Im zweiten Schritt wird das Ergebnis ganzgradig auf- oder abgerundet. In diesem Fall wird abgerundet:
(12) ![]()
Als letztes wird die Rechenortlänge bestimmt. Dazu wird aus dem gerade gewonnenen ganzgradigen LHA der Grt entfernt. Als Ergebnis verbleibt ein HO 249-gerechter Rechenort:
(13) ![]()
Bei westlichen und damit negativen Schiffslängen wird der Rechenort nicht als LHA – Grt berechnet, sondern als Grt – LHA. Damit sind alle Vorbereitungen abgeschlossen und der Navigator wird mit den folgenden drei Eingangswerten in die Tafel gehen:
- LAT = 39°N
- DECLINATION = 14°N
- LHA = 334
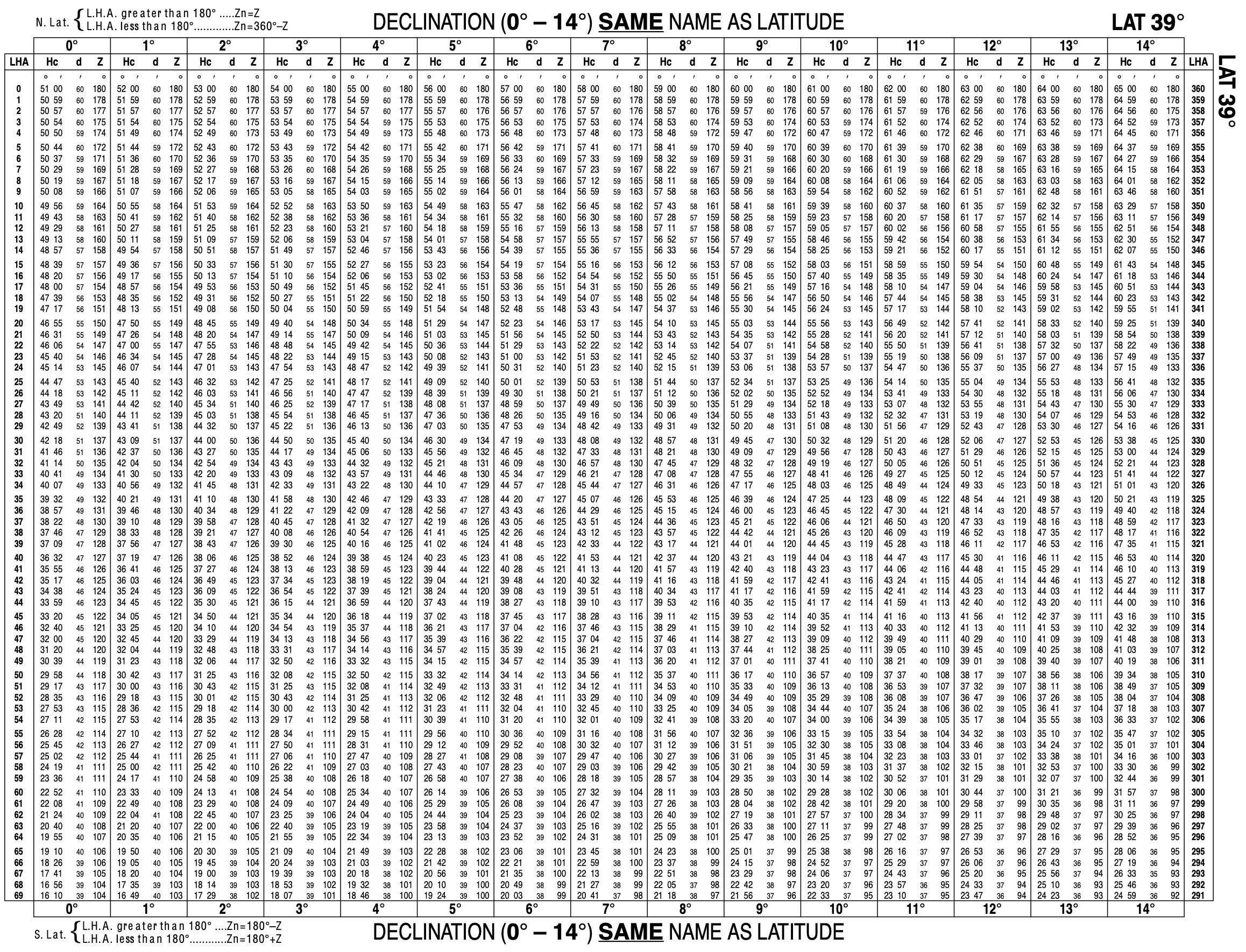
In der HO 249 gibt es die Seiten SAME und CONTRARY. Wenn Breite und DECLINATION auf derselben Halbkugel der Erde liegen, dann sind die Seiten mit der Bezeichnung SAME zuständig. In diesem Beispiel ist das der Fall, denn Deklination und Breite sind beides nördliche Breiten. Band 3 der HO249 beginnt mit Seite LAT 39 und so beginnt die Suche gleich auf dieser ersten Seite. Der Navigator sucht in der Spalte die Zeile für LHA = 334 und geht dann in dieser Zeile in die Deklinationsspalte 14°, die er gleich daneben findet. Aus dieser Spalte lieste er aus:
Hc = 56°06′, d = 47 und Z = 130°
Links oberhalb und unterhalb der Tabelle sind Regeln zur Fallunterscheidung des Azimuts Z angegeben. Links oben steht N. LAT. {L.H.A greater then 180° ….. Zn = Z. Weil der Standort auf nördlicher Breite liegt und LHA größer als 180° ist, ist das das ausgelesene Z das richtige Azimut.
Es müssen aber noch die abgeschnittenen Minutenanteile der Deklination berücksichtigt werden. Dafür gibt es auf Seite 344 der HO 249 die „TABLE 5. — Correction to Tabulated Altitude for Minutes of Declination“. Mit dem in dieser TABLE 5 gelisteten Wert wird Hc korrigiert. Dazu geht der Navigator in der oberen Reihe auf den ausgelesenen Wert d = 47 und liest in der Zeile der abgeschnittenen Minutenanteile, es waren 26,0′ den Wert 20′. Sollte das ausgelesene d negativ sein dann muss auch der aus Tabelle 5 entnommene Wert ein negatives Vorzeichen erhalten. Dieser Wert addiert er zur ausgelesenen Höhe Hc und bekommt als Ergebnis die korrigierte berechnete Höhe von Hc = 56° 06′ + 20′ = 56°26′.
Table 5 Pub. No. 249
Jetzt kann die Standlinie in der üblichen Weise konstruiert werden, denn Rechenortbreite LAT, Rechenortlänge ![]() , das Azimut Z mit 130° und die Höhendifferenz zwischen der beobachteten Höhe und der korrigierten berechneten Höhe sind bekannt:
, das Azimut Z mit 130° und die Höhendifferenz zwischen der beobachteten Höhe und der korrigierten berechneten Höhe sind bekannt:
- LAT = 39° N
- λRO = 4° 23,5 E
- Z1 = 130°
- Hc = 56° 26,0′ (beobachtete Höhe)
- Hm= 56° 41,02′ (mit Sextant gemessene Höhe)
- ΔH = Hc – Hm = -15,02′ = -15,02 NM
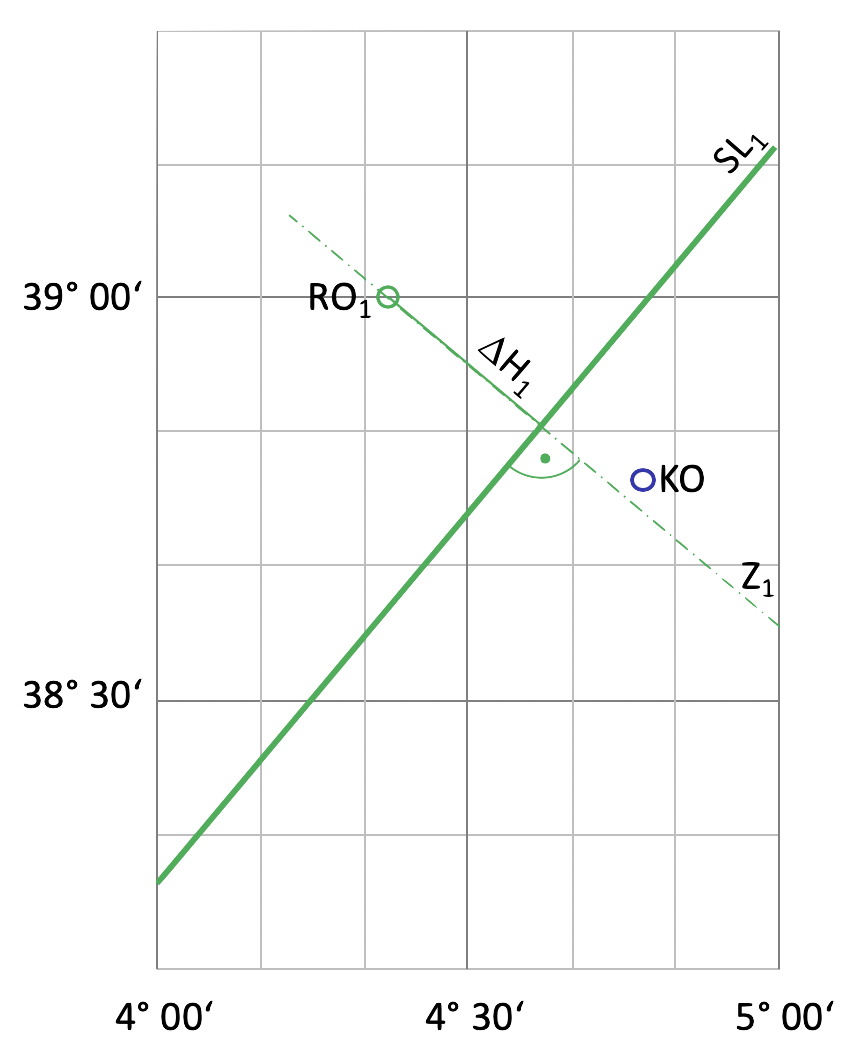 Die gemessene Höhe ist um 15,02′ größer als die berechnete. Der eigene Standort ist also um 15,02 NM dichter an der Sonne als der Rechenort. Die Strecke vom Rechenort bis zum Bildpunkt der Sonne muss um diese 15,05 NM verkürzt werden. An dieser Stelle darf man sich nicht irren. Dadurch hat es schon Unfälle gegeben. Immer daran denken: dichter dran – der Blick geht hoch.
Die gemessene Höhe ist um 15,02′ größer als die berechnete. Der eigene Standort ist also um 15,02 NM dichter an der Sonne als der Rechenort. Die Strecke vom Rechenort bis zum Bildpunkt der Sonne muss um diese 15,05 NM verkürzt werden. An dieser Stelle darf man sich nicht irren. Dadurch hat es schon Unfälle gegeben. Immer daran denken: dichter dran – der Blick geht hoch.
Die erste Standlinie kann jetzt gezeichnet werden. Auf der Leerkarte wird zuerst der Rechenort als Kreuz oder Punkt markiert. Den Ort findet der Navigator mit dem Zirkel, an dem er eine Spanne von 36,5 mm einstellt. Diese Weite ergibt aus den Bogenminuten der mit der Gl. 3 errechneten Länge von 23,5′ und dem gewählten horizontalen Maßstab von 15,54 mm/ 10′ und beträgt somit 36,53 mm. Sie wird auf dem 39° Breitenkreis nach rechts bzw. Ost abgetragen. Das ist dann die Position von Rechenort 1 (RO1).
Jetzt kann er durch diesen Rechenort im Winkel von 130° eine Linie ziehen. das ist dann der Azimutstrahl Z1, auf der jetzt die Höhendifferenz ΔH von -15,02′ abgetragen werden muss. Dazu nimmt der Navigator eine Spanne von 30 mm in den Zirkel und verkürzt damit die Länge des Azimutstrahls zwischen Rechenort und Bildpunkt. Die 30 mm entsprechen dem vertikalen Maßstab der Leerkarte von 20 mm/10′. Das Ergebnis ist im nebenstehenden Bild zu sehen.
Eine Standlinie ist schon etwas wert. Das hatte schon Thomas Sumner erkannt und beschrieben. Man kann davon einen sicheren Kurs auf ein Ziel an Land ableiten oder in sicherem Abstand an einer unsichtbaren Küste entlangsegeln. Ein Standort ergibt sich jedoch erst aus dem Schnittpunkt von zwei Standlinien. Besonders bequem ist es, wenn als zweite Standlinie die Mittagsbreite benutzt werden kann. Dabei ist es egal, ob zuerst eine Standlinie mit der HO 249 und danach die Mittagsbreite ermittelt wird, oder umgekehrt. Wichtig ist dabei nur, dass ein genügenden zeitlicher Abstand eingehalten wird, damit die Standlinien nicht schleifen, d. h., der Winkel zwischen den Linien zu spitz ist. Ein Winkel von >30° sollte mindestens eingehalten sein.
Wird zwischen den Beobachtungen eine Strecke zurückgelegt, dann sind zum Zeitpunkt der zweiten Beobachtung Distanz und Kurs dieser Ortsveränderung als Pfeil (Versegelungsvektor) im richtigen Maßstab und im richtigen Kurs an einen beliebigen Punkt der ersten Standlinie anzulegen. Daraufhin wird die Standlinie parallel verschoben, bis sie durch die Spitze des gezeichneten Pfeils verläuft. Der Standort ergibt sich dann als Schnittpunkt zwischen der verschobenen und der zweiten Standlinie.
Die zweite Standlinie
Der Einfachheit halber soll angenommen werden, dass Totenflaute herrscht und die erste Standlinie nicht verschoben werden muss. Um 12:55:33 beobachtet der Navigator die Sonne zum zweiten Mal und misst dabei einen Kimmabstand von 60° 25,4′. Nach Berichtigung dieser Sextantenablesung wird eine beobachtete Höhe von 60° 36,91′ festgestellt. Die folgenden Aufstellungen ergeben sich dann wieder aus dem Nautischen Jahrbuch:
- Grt um 12:00 UT1 0° 39,0′
- Zuwachs für 55m 33s: 13° 53,3′
- Grt um 9:55:51 UT1: 14° 32,3′
Für die Verbesserung der Deklination um 12:00 UTC gilt in diesem Fall dasselbe wie nach der ersten Beobachtung. Einen Unterschied von 0,8′ stellt man auch für die benachbarten Tage fest und die Beobachtung erfolgte in derselben Minute 55. Damit beträgt die Verbesserung auch hier 0,7′ N.
- δ um 12:00 UT1: 14 27,6′ N
- Vb: 0,7′ N
- Deklination δ 14° 28,3′ N
Im Anschluß daran müssen LHA und Rechenort berechnet werden, was mit den Gleichungen 1 bis 3 geschieht:
![]()
![]()
![]()
Daraus ergeben sich wieder die Werte, mit denen der Navigator in die Tafel einsteigen kann:
- LAT = 39° N
- DECLINATION = 14° N
- LHA = 19°
Dort liest er aus:
Hc = 59°55′, d = 51, Z = 141
Der LHA ist kleiner als 180°, daraus folgt für das Azimut Z = 360° – 139° = 221°.
TABLE 5 liefert mit d = 51 für die weggelassenen 28′ der Deklination einen Korrekturwert von 24′ zur Erhöhung von Hc. Wir haben jetzt:
- LAT = 39° N
- λRO = 4° 27,2 E
- Z1 = 221°
- Hc = 60° 19,0′ (aus Tafel berechnete Höhe)
- Hm= 60° 37′ (beobachtete Höhe)
- ΔH = Hc – Hm = -18′ = -18 NM
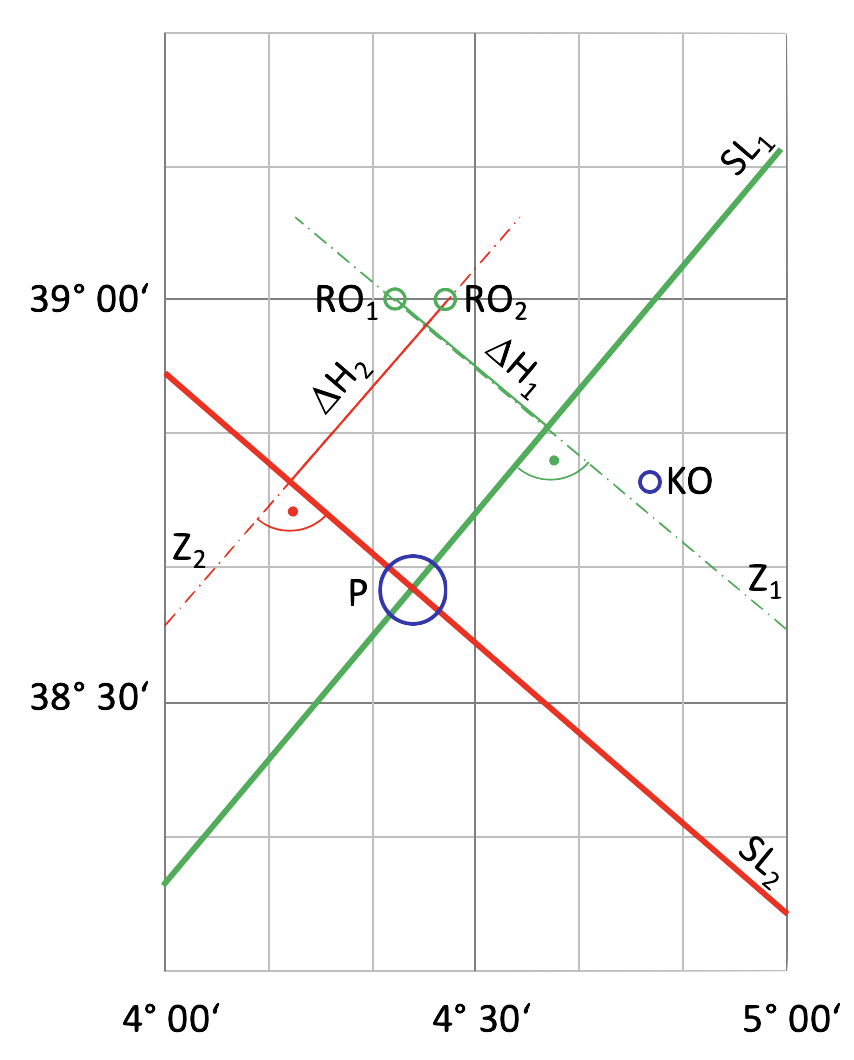 Mit diesen Werten kann jetzt eine zweite Standlinie konstruiert werden. Der Standort ist der Schnittpunkt der beiden Standlinien. Auch hier ist die gemessene Höhe größer als die berechnete. Der eigene Standort, von dem aus die Beobachtung erfolgte, ist also um 18 NM dichter am, Bildpunkt der Sonne als der Rechenort. Der Navigator beginnt wie zuvor mit dem Rechenort, der auf derselben Breite, aber noch etwas östlicher liegt. Sein Abstand beträgt aufgrund des Maßstabes von 15,54 mm/ 10′ in der Horizontalen 42,3 mm vom 4° Längengrad.
Mit diesen Werten kann jetzt eine zweite Standlinie konstruiert werden. Der Standort ist der Schnittpunkt der beiden Standlinien. Auch hier ist die gemessene Höhe größer als die berechnete. Der eigene Standort, von dem aus die Beobachtung erfolgte, ist also um 18 NM dichter am, Bildpunkt der Sonne als der Rechenort. Der Navigator beginnt wie zuvor mit dem Rechenort, der auf derselben Breite, aber noch etwas östlicher liegt. Sein Abstand beträgt aufgrund des Maßstabes von 15,54 mm/ 10′ in der Horizontalen 42,3 mm vom 4° Längengrad.
Durch diesen Rechenort wird dann das Azimut Z2 in einem Winkel von 221° gezeichnet. Nach Verkürzen des Azimutstrahls um 18 NM durch Abtragen der Höhendifferenz von 18 NM = 36 mm, ausgehend vom Rechenort 2 in Richtung Bildpunkt, liegt die Position fest, in welcher die Standlinie senkrecht durch den Azimutstrahl geht. Der Standort ist der Schnittpunkt der beiden Standlinien.
Der Standort muss jetzt aus der Zeichnung herausgelesen werden. Mit einem Zirkel misst der Navigator einen östlichen Abstand von 37,7 mm vom 4° Meridian und nach Norden einen Abstand von 18,1 mm von 38° 30′ Breite. Diese Strecken müssen jetzt mit den Maßstäben der Karten multipliziert werden. Diese betragen in der Vertikalen 1’/2 mm und in der Horizontalen 1’/1,555 mm. Der horizontale Maßstab wird bekanntlich vom Kosinus der Rechenortbreite bestimmt. Wenn in der Vertikalen 10′ = 20 mm sind, dann beträgt der 10′ Meridianabstand in der Horizontalen 20 mm · cos(39°) = 15,55 mm. Somit ist der Standort bestimmt und beträgt
38° 39,05′ N / 004° 24,26′ E.
Nach der Methode von Gauß wird mit den gleichen Daten ein Standort von
39° 38,46′ N / 004° 24,86′ E.
errechnet. Daraus folgt, dass der mit Gauß berechnete Standort jeweils etwa 1 km südlicher und östlicher liegt. Diese Unterschiede sind nicht mit Standortabweichungen gleichzusetzen. Sie beruhen einzig und allein auf der Rechenmethode. Die Gauß Methode rechnet sehr präzise mit der Erde als ideale Kugel, was sie aber nicht ist, denn sie hat an den Polen geringfügige Abplattungen. Abgesehen davon, ein egal wie berechneter Standort weicht größtenteils infolge von Fehlern bei der Messung von Höhe und Zeit vom wahren Standort ab und diese Abweichungen betragen in der Regel mehr als 2 NM bzw 4 km. Wenn die Rechenmethode einen Fehlereinfluß von 0,5 NM bewirkt und die Messunsicherheit 2 NM ausmachen, dann errechnet sich daraus nach dem Fehlerfortpflanzungsgesetz ein Gesamtfehler von Wurzel aus (0,52 + 22) und das sind 2,06 NM. Der Fehler durch die Rechenmethode ist also vernachlässigbar, wenn er im Bereich von 0,5 NM liegt. Setzt man nämlich den Fehler durch die Rechenmethode zu null, dann ist man nur um 0,06 NM genauer. Das sind natürlich statistische Betrachtungen, die sich auf keinen Einzelfall beziehen, sondern für eine größere Menge gelten. Die Tafelmethode ist also durchaus eine brauchbare Methode zur Standortbestimmung mit einem Sextanten.
Anfertigen von Leerkarten
Für beide Methoden, ob nach Hilaire klassisch oder mit Tafeln navigiert wird, sind Leerkarten hilfreich. Das schont die richtigen Seekarten, vor dem ständigen ausradieren der vielen Bleistiftlinien. Ihre Konstruktion ist einfach und im Bild 7 dargestellt. Bei der Konstruktionsart links zeichnet man zuerst die Achsen eines Koordinatensystems, wobei die senkrechte Achse rechts oder links angeordnet sein kann. Danach werden die Breiten eingezeichnet. Dabei startet man vielleicht 15’ südlich des Koppelortes. Beispielsweise liegt der gegisste Standort auf 38° 15’ N, dann startet man bei 38° und zeichnet alle 5’ eine neue Breite ein. Wenn 5 mm 1,0 Bogenminute bzw. 1,0 Seemeile sein soll, dann ist der einzuzeichnende Breitenabstand 25 mm. Man kann aber auch beliebig andere Maßstäbe wählen. Vom Ursprung aus wird jetzt eine Gerade im Anstiegswinkel der Breite eingezeichnet, für die das Mertcator-Netz gezeichnet werden soll. Im Bild ist das die blaue Linie. Jetzt wird ein Zirkel in den Koordinaten-Nullpunkt gestochen und damit die an der vertikalen Achse abgegriffene Breite in der jeweiligen Zirkelspanne auf die Schräge übertragen. Dort wo sich der Bogen mit der 38° Schräge kreuzt, wird eine senkrechte Linie eingezeichnet. Diese Linien sind Meridiane im Abstand von 5’. Auf einer Breite von 38° sind das aber nur 5 ⋅ cos 38° = 3,94 nm.
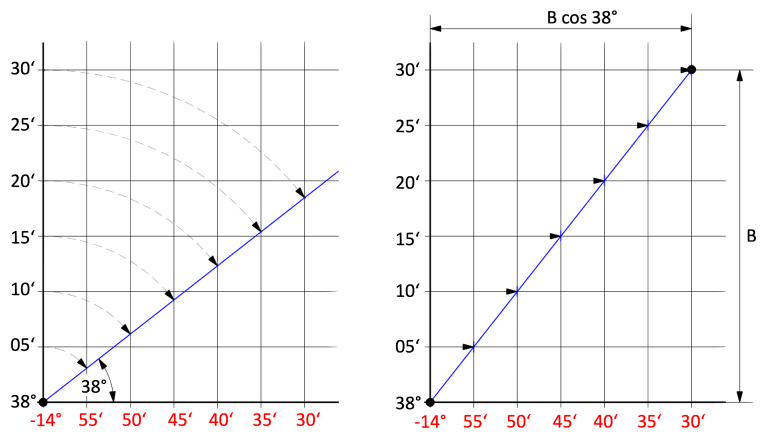
Bei der Konstruktionsart auf der rechten Seite zeichnet man ebenfalls zuerst die Achsen eines Koordinatensystems, wobei auch hier die senkrechte Achse rechts oder links angeordnet sein kann. Danach werden die Breiten eingezeichnet. Startpunkt und Abstand werden nach gleichen Gesichtspunkten vorgegeben wie auf der linken Seite. Jetzt wird die Länge der skalierten Breitenskala ausgemessen. Wenn ein Abstand von 2,5 cm pro 5’ zwischen den Linien vorgegeben ist und die Breitenskala von 38° bis 38° 30’ reicht, dann ist ihre Länge 15 cm. Jetzt wird auf der obersten Breitenlinie ein Abschnitt von B ⋅ cos 38° = 15 cm ⋅ 0,788 = 11,82 cm abgetragen. Vom Koordinatenursprung bis zu diesem Punkt wird jetzt eine Diagonale eingezeichnet. Im Bild ist das ebenfalls eine blaue Linie. An allen Stellen, wo jetzt diese Diagonale von den 5’ Breitenlinien geschnitten wird, entstehen Punkte, an denen die Meridianlinien im 5’ Abstand eingezeichnet werden.
Beginn- oder Ende der Bemaßung der horizontalen Achse ist natürlich breitenunabhängig.
Links:
nach oben ♦ Die Sonne am Himmel ♦ Mittagsbreite und Chronometerlänge ♦ Gauß und das Zweihöhenproblem ♦ Thomas H. Sumner, Begründer der Standliniennavigation ♦ Navigieren mit Excel ♦ Ein wenig Sextantenkunde ♦ Sextantentest Mark 25 ♦ Downloads ♦ Home