
Standort mit Sextant, Handy oder Tablet – ganz stressfrei, kein Nautisches Jahrbuch, kein Rechnen, kein Zeichnen, kein Schätzort und mathematisch präzise.
In diesem Beitrag erstellen wir ein Excel Sheet, mit dem Standorte auf hoher See nach der analytischen Methode von Carl Friedrich Gauß mit hoher Genauigkeit bestimmt werden können. Excel und Word von Microsoft sind weit verbreitete Büroprogramme, die fast jeder auf seinem heimischen Computer hat. Zwar kann auch ein Handy den GPS Standort aus Satellitensignalen anzeigen, doch darum geht es nicht. Es ist schon etwas anderes, wenn man selbst die Berechnungsformeln in eine Excel Tabelle bringt und dabei lernt, wie ein Standort mit einem Sextanten aus dem Lauf der Sonne heraus bestimmt werden kann. Nebenbei lernt man auch gleich Excel zu verstehen, was im normalen Leben gewiss seine Vorteile hat.
Als es noch keine Computer gab, waren grafische Methoden die beste Möglichkeit, einen Standort auf See zu bestimmen. Diese kamen in der Mitte des 19. Jahrhunderts auf, nachdem Kapitän Thomas H. Sumner die Standlinie erfunden hatte. Sie vermittelten eine recht gute Sicherheit und haben sich rasch verbreitet. Doch heute haben wir Computer und da wäre es völliger Unfug, mit großem Aufwand eine solche grafische Methode digitalisieren zu wollen, die sowieso nur eine Näherungslösung ist, wo es doch viel ältere analytische und genaue Methoden von Leonhard Euler und Carl Friedrich Gauß gibt.
Unsere Excel-Navigationsdatei enthält folgende Funktionen:
- grafisch ansprechende Eingabe und Ausgabe von Daten
- Standortbestimmung nach Carl Friedrich Gauß (1809)
- Berücksichtigung einer Versegelung nach Douwes (um 1750)
- automatische Sextantenbeschickung ab Höhen von 7°
- Berechnung des Greenwichwinkels Grt und der Deklination
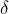
- Standortgrafik
Bei Benutzung dieser Navigations-Datei erfolgt die Sextantenbeschickung automatisch und auch die Sonnenephemeriden Grt und ![]() berechnen wir selbst. Wir brauchen deshalb kein nautisches Jahrbuch, sondern benutzen stattdessen ein paar Formeln. Ein Anwender der Excel Datei muss nichts von Astronomie oder Mathematik verstehen.
berechnen wir selbst. Wir brauchen deshalb kein nautisches Jahrbuch, sondern benutzen stattdessen ein paar Formeln. Ein Anwender der Excel Datei muss nichts von Astronomie oder Mathematik verstehen.
Der Vorteil einer Sextantennavigation ist, dass der Kartenplotter außerhalb einer sichtbaren Küste ausgeschaltet bleiben kann. Das spart nicht nur Strom, es lenkt die Aufmerksamkeit wieder stärker auf die Umgebung. Sind die Gewässer komplizierter, kann gern wieder der Kartenplotter in Betrieb gehen. Nötig ist jedoch eine Papierkarte zur Orientierung und Absetzung eines Kurses. Wir beschränken uns auf das Navigationsgestirn Sonne, denn die Sonne kann mit keinem anderen Gestirn verwechselt werden.
Die Methode von Gauß rechnet sehr präzise. Trotzdem muss mit Standortabweichungen gerechnet werden, die vor allem auf Ungenauigkeiten bei der Höhen- und Zeitmessung beruhen. Deshalb sollte hier viel geübt werden. Ein Anfänger kann froh sein, wenn er einen Standort auf 5 Meilen genau bestimmt. Ein Könner bringt es bei ruhiger See auf ein bis zwei Meilen Standortabweichung.
Man könnte meinen, dass ein derartig selbst gemachtes Programm ohne Nautisches Jahrbuch, mit selbst berechnetem Greenwichwinkel und selbst berechneter Deklination nicht genau ist. Doch das ist Unsinn. Das Programm in diesem Beitrag ist genauer als das bekannte und weit verbreitete Höhenverfahren von Saint Hilaire.
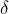 gegenüber einer fehlerfreien Berechnung.
gegenüber einer fehlerfreien Berechnung.Bild 1 zeigt die für das Jahr 2021 ermittelten Standortabweichungen, die sich aus dem Unterschied zwischen den selbst berechneten Daten von Greenwichwinkel Grt und Deklination ![]() und den Daten aus einem amtlichen Nautischen Jahrbuch ergeben würden. Die Abweichungen kommen zustande, weil die Einflüsse des Mondes und der großen Planeten in den eigenen Berechnungen nicht erfasst wurden, damit der Rechenumfang nicht ausufert. Sie sind jedoch niemals größer als eine halbe Meile. Was bedeutet das? Ein guter Navigator bringt es in der astronomischen Standortbestimmung auf einem nicht oder nur wenig schwankenden Deck auf eine Standortabweichung von 2 NM. Nach dem Fehlerfortpflanzungsgesetz addieren sich Einzelfehler jedoch geometrisch. Dafür ein Beispiel
und den Daten aus einem amtlichen Nautischen Jahrbuch ergeben würden. Die Abweichungen kommen zustande, weil die Einflüsse des Mondes und der großen Planeten in den eigenen Berechnungen nicht erfasst wurden, damit der Rechenumfang nicht ausufert. Sie sind jedoch niemals größer als eine halbe Meile. Was bedeutet das? Ein guter Navigator bringt es in der astronomischen Standortbestimmung auf einem nicht oder nur wenig schwankenden Deck auf eine Standortabweichung von 2 NM. Nach dem Fehlerfortpflanzungsgesetz addieren sich Einzelfehler jedoch geometrisch. Dafür ein Beispiel
Man weiß ja nicht, in welcher Höhe diese maximalen Einzelfehler gerade auftreten und ob sie dann positiv oder negativ sind. Der worst case, beide sind gerade maximal positiv oder beide sind gerade maximal negativ ist eine Abweichung des Standortes vom Rechenergebnis von +2,44 NM, dürfte aber äußerst selten eintreten. Für dieses Beispiel gilt eine mittlere zu erwartende Standortabweichung von
![]() .
.
Wenn jetzt der rechnerische Fehler null wird, weil ein hochgenaues amtliches nautisches Jahrbuch benutzt wird, dann bewirken nur noch die Messfehler eine Standortabweichung und die beträgt dann
![]() .
.
Der Unterschied zwischen diesen beiden Ergebnissen beträgt 0,063 NM oder 120 Meter und das sind 3,2%, die auf die im Bild 1 gezeigten Abweichungen zurückzuführen sind.
Dieser geringe Anteil sinkt sogar drastisch, sobald andere Fehler zunehmen. Die im Bild dokumentierten Abweichungen infolge selbst berechneter Sonnenephemeriden haben somit überhaupt keine praktische Bedeutung. Das Höhenverfahren von Saint Hilaire besitzt in der Regel größere Rechenfehler, nicht durch fehlerhafte Ephemeriden, sondern durch die Ungenauigkeit einer Standortschätzung und unpräzise ausgeführte grafische Arbeiten. Da mag es vielleicht hilfreich sein, wenn die Daten eines amtlichen nautischen Jahrbuchs noch ein bisschen genauer sind, als die selbst berechneten.
Interessant ist die Welligkeit der im Bild 1 gezeigten Kurven. Der höherfrequente Anteil der Welligkeit ist durch die Mondzyklen bedingt, denn es ist nicht der Erdmittelpunkt, der auf seiner elliptischen Bahn die Sonne umkreist. Vielmehr kreist der Schwerpunkt des Massensystems Erde-Mond um die Sonne, wobei dieser Schwerpunkt 4760 km vom Erdmittelpunkt entfernt ist. Dadurch “eiert” der Erdmittelpunkt auf seiner Bahn um die Sonne hin und her, entfernt sich von der Sonne und nähert sich dieser wieder an. Eine Schwingungsperiode dauert dabei so lange wie ein Mondumlauf, also etwa einen Monat.
Der niederfrequente Anteil, zeigt die Annäherung der Erde auf ihrer jährlichen Umlaufbahn um die Sonne an die großen Planeten, deren Umlauf um die Sonne wegen ihrer großen Masse einige tausende Jahre betragen kann. Diese großen Wellen, wie sie Bild 1 zeigt, werden wir in den nächsten Erdjahren also immer in denselben Monaten beobachten können.
Alle Berechnungen sind ziemlich anspruchslos. Sämtliche Formeln liegen vor und müssen nur noch eingegeben werden. Schwieriger ist schon die Gewöhnung an die Notation von Excel. Die hier beschriebene Datei hat nur eine Größe von 55 KB und kann hier als
heruntergeladen werden. Das Kennwort, das zur Bearbeitung gebraucht wird lautet change. Das Passwort dient nur zum Eigenschutz, damit während der Benutzung keine Formeln mit irgend welchen Werten überschrieben werden. So kann jeder die Datei verändern und nach eigenen Ansprüchen erweitern.
Eingabenmaske
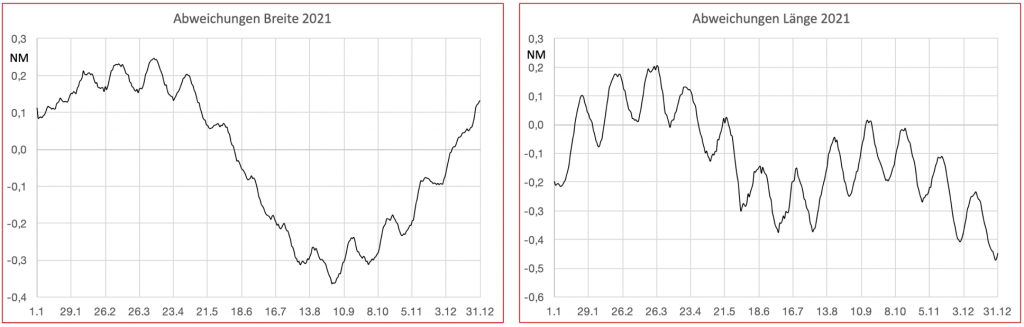
Wer ein derartiges Projekt plant, sollte als erstes eine Eingabenmaske anlegen, damit er weiß, was alles zu erledigen ist. Ein Beispiel dafür ist im Bild 2 gezeigt. Der größte Arbeitsanteil dürfte dabei auf die Rahmengestaltung und Textformatierung entfallen.

Bild 2: Displayanzeige der Eingabenmaske der Excel Datei excel-cop-navigation
Für Eingaben und Ausgaben wurden fünf Blöcke angelegt. Die Felder mit dem grauem Hintergrund sind nicht geschützt. Wird nämlich das ganze Arbeitsblatt mit einem Passwort geschützt, dann bleiben nur diese Felder für einzugebende Daten beschreibbar. Alle anderen sind dann vor unbeabsichtigter Veränderung gesichert.
Im obersten Block werden Einstellungen vorgenommen. Indexberichtigungen können für jede Beobachtung getrennt eingetragen werden. Das ist bei Verwendung von Plastiksextanten von Vorteil, weil diese sehr temperaturabhängig reagieren und sich der Wert zwischen den Beobachtungen ändern kann. Als Indexberichtigung wird der negative Wert des festgestellten Indexfehlers eingetragen. Bei Metallsextanten wird in beide Felder die gleiche Zahl eingetragen. Eine Überprüfung, ob der Indexfehler noch aktuell ist, sollte monatlich erfolgen. Auch der Sonnenrand kann für jede Beobachtung extra angegeben werden. Es könnte ja sein, dass für eine der beiden Beobachtungen der obere oder untere Rand der Sonne von einer Wolke verdeckt ist. Mit Standortwahl wird festgelegt, ob man nördlich oder südlich von der Deklinationsbreite segelt. In unseren Breiten und dazu zählt auch der gesamte Mittelmeerraum, steht dort immer ein N.
In den Feldern Messung 1 und Messung 2 werden Datum, Zeit und Sextantenablesung eingetragen. Eine durch Koppelnavigation festgestellte Ortsveränderung in der Zeit zwischen der ersten und den weiteren Beobachtungen wird unter Versegelung eingetragen. Die im Bild 2 vorgenommenen Eintragungen sind als Beispiel zu verstehen, auf das im Folgenden immer Bezug genommen wird.
Der Standort wird sofort nach Eintragung der Daten unter Messung 2 berechnet und als Ergebnis angezeigt. Darunterstehend wird auch die Zeit des Schiffsmittags ausgegeben. Diese steht allerdings erst nach einer zweiten Beobachtung zur Verfügung.
Sextantenbeschickung
Ein Wert, der an Gradbogen und Trommel eines Sextanten abgelesen wird ist nicht der Kimmabstand bzw. die beobachtete Höhe. Diese erhält man erst durch Addition von Korrekturwerten, die zum Ausgleich von Kimmtiefe und Refraktion dienen. Weitere Korrekturen betreffen den Ausgleich des unterschiedlichen Durchmessers der Sonnenscheibe, die ist nämlich im Winter größer. Das ist dann die sogenannte Zusatzbeschickung. Außerdem ist eine Korrektur eines Indexfehlers des verwendeten Sextanten erforderlich.
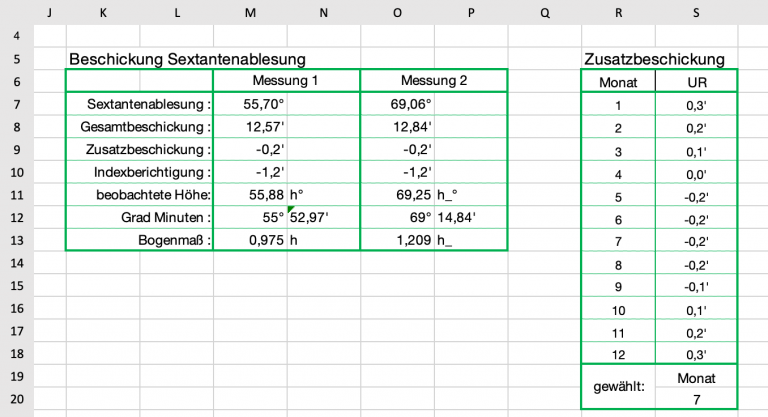
Bild 3 zeigt das Sextantenbeschickungs-Modul. Der Sinn von Tabellenkalkulationen besteht darin, dass die in den Zellen angezeigten Daten nicht nur eingegebene Werte sind, sondern vor allem Ergebnisse von Formeln, die sich auf andere Zellen beziehen. So enthält die Zelle M7 die Formel
=G14+H14/60.
Das ist die vom Gradbogen abgelesene Gradzahl addiert mit der an der Trommel abgelesenen und durch 60 dividierten Anzahl der Bogenminuten und damit die dezimale Sextantenablesung. Das war jetzt ganz einfach. Zelle M8 mit der Gesamtbeschickung sieht schon komplizierter aus:
=16-(55*TAN(BOGENMASS(90-M7))/60-55/1000*(TAN(BOGENMASS(90-M7)))^3/60+
1,777*WURZEL(G8))
Das ist in Excel Schreibweise die Summe der folgenden beiden nachstehenden Formeln, die für eine Gesamtbeschickung gebraucht werden, nämlich
(1) ![]()
(2) ![]()
Hierin ist AH die Augeshöhe. Diese Summe wird von 16’ subtrahiert, denn das ist der halbe mittlere Sonnendurchmesser. Bei einer Beobachtung wird die Sonne meist mit ihrem Unterrand, manchmal aber auch mit ihrem Oberrand auf den Horizont gesetzt und nicht mit ihrer Mitte und das muss mit den 16’ berücksichtigt werden. Für die Zusatzbeschickung wird eine Datenbank-Auszugsfunktion gebraucht, denn die zu verwendenden Werte sind in einer Tabelle von R6 bis S18 tabelliert und wir brauchen einen Auszug daraus. Diesen erhalten wir mit der Funktion
=DBAUSZUG(Datenbank;Datenbankfeld; Suchkriterien).
Darin ist Datenbank der Zellenbereich der gesamten Tabelle. Datenbankfeld ist die Tabellenspalte, aus der wir einen Wert erhalten wollen, also hier die zweite Spalte. Dort wird eine 2 für zweite Spalte eingetragen oder der Namen der Kopfspalte „UR“, der für Unterrand steht. Suchkriterien sind zwei übereinander anzuordnende Felder, wobei das obere den Namen der Suchspalte angibt und das untere die Suchzeile. Gewählt wurden die zwei Zellen S19 und S20. Darin werden der Spaltenname “Monat” und darunter die Zeile mit dem Monat angegeben. In die Zelle K16 wird die Formel =MONAT(G12) eingetragen. Dadurch steht dort immer der Monat, in dem die Beobachtung erfolgt. In unserem Beispiel ist es eine 7 für den Monat Juli, so dass in der Tabelle in der Monatszeile 7 in der zweiten Spalte der Wert -0,2′ als Datenbankauszug gefunden wird.
In den Feldern H6 und H7 konnte angegeben werden, ob die Sonne mit dem Unterrand oder dem Oberrand auf den Horizont gesetzt wurde. Wird der Oberrand benutzt, dann muss der Sonnendurchmesser von 32′ subtrahiert werden. Die Datenbankfunktion muss also mit einer WENN – DANN Funktion verknüpft werden. Damit sieht die Berechnung der Zusatzbeschickung für die erste Beobachtung so aus:
=WENN(H6=”U”;DBAUSZUG(R6:S18;2;S19:S20);
WENN(H6=”O”;-(32+DBAUSZUG(R6:S18;2;S19:S20));#NV)))
Für die zweite Beobachtung wird für die Zusatzbeschickung die anstelle der Zelle 6 die Zelle H7 benutzt. Es könnte schließlich sein, dass zum Zeitpunkt der zweiten Beobachtung der Unterrand der Sonne von Wolken verdeckt ist.
Die beobachtete Höhe ist die Summe aller vorstehenden Zellen M7 bis M9 bzw. O7 bis O9 plus der Indexberichtigung des Sextanten. Das Ergebnis wird in den Zeilen 11 und 13 als Gradmaß und als Bogenmaß ausgegeben. Die Excel-Namen sind h° und h_° für die beobachteten Höhen in der ersten bzw. zweiten Beobachtung im Gradmaß und h bzw h_ im Bogenmaß. Die Variable #NV in der Formel für die Zusatzbeschickung steht steht für “nicht verfügbar”, wenn anstelle von “O” oder “U” irgend etwas anderes eingetragen wurde.
Sun Almanac
Wer astronomisch navigieren will, der braucht normalerweise ein Nautisches Jahrbuch, aus dem er die Position des Bildpunktes des beobachteten Gestirns entnehmen kann. Das sind die Positionen, an denen das Gestirn oder die Sonne gerade im Zenit steht. Das nautische Jahrbuch wurde in Deutschland vom BSH das letzte Mal für das Jahr 2020 herausgegeben. Damit ging nach 170 Jahren eine alte Tradition zu Ende. Es ist aber, wie eingangs gesagt, kein Hexenwerk, sich diese Daten zumindest für das Navigationsgestirn Sonne selbst zu berechnen. Dazu benötigt man die Bahnelemente des Umlaufs der Erde um die Sonne.
Das Problem dabei ist nur, dass kein Jahr mit derselben Sekunde beginnt wie das nächste. Es existiert kein ganzzahliges Verhältnis zwischen der Zahl der Eigenrotationen und dem Umlauf der Erde um die Sonne und somit gibt es auch keinen Kalender, dessen Tage genau auf ein Jahr passen. Einen gewissen Ausgleich erreicht man zwar mit Schalttagen, die in der Regel alle vier Jahre in den Kalender eingefügt werden. Doch auch dann muss man über die Jahrhunderte gesehen mal einen zusätzlichen Schalttag einführen oder auch mal einen ausfallen lassen.
Daraus ergibt sich die Frage, wann die Zeitmessung eigentlich angefangen hat. Das war genau 4713 v. Chr., also vor 6735 Jahren. Damit man jetzt nicht immer bis dahin zurückrechnen muss, hat man Etappen festgelegt und die zuletzt zurückgelegte Etappe endete am 1. Januar 2000 um 12:00:00 UT. Für dieses Referenzdatum wurden die aktuellen Werte der Bahnelemente der Erde als lineare Gleichungen abgelegt. Die Gleichungen haben alle die Form Y = A + B ・ T, wobei A der Wert des Parameters am Referenzdatum um 12:00:00 UT ist und das Produkt B ・ T die mit den zukünftigen Tagen T zu erwartenden Änderungen beschreibt. Die Bahnelemente lauten:
|
1 |
|
Mittlere Länge in Grad ab Perihel |
|
2 |
|
Länge des Perihels in Grad |
|
3 |
|
numerische Exzentrizität |
|
4 |
|
Schiefe der Ekliptik in Grad |
Es ist tatsächlich so, dass wir mit Hilfe dieser Gleichungen in der Lage sind, die Stellung der Erde bezüglich der Sonne auf die Sekunde genau herausfinden zu können. Wir können also genau ausrechnen, an welchem Punkt der Erde zu einem ganz bestimmten Datum und zu einer ganz bestimmten sekundengenauen Zeit, die Sonne gerade im Zenit steht. Um den Greenwichwinkel Grt und die Deklination ![]() der Sonne zu bestimmen, brauchen wir also kein Nautisches Jahrbuch mehr, sondern nur eine kleine Rechnung in Excel, wie sie im Bild 4 gezeigt ist.
der Sonne zu bestimmen, brauchen wir also kein Nautisches Jahrbuch mehr, sondern nur eine kleine Rechnung in Excel, wie sie im Bild 4 gezeigt ist.
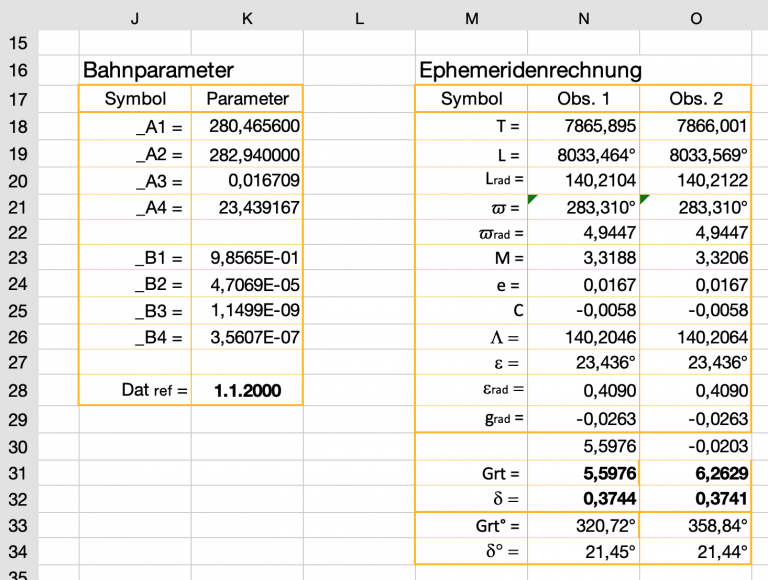
Wir fangen damit an, die Zeit auszurechnen, die vom 1. Januar 12:00:00 UT1 bis zu der Sekunde vergangen ist, in der wir die Sonne im Fernrohr unseres Sextanten auf den Horizont gesetzt haben. Das geht ganz einfach. In der Excel Datei lautet der Name für das in K28 stehende Referenzdatum ref. Datum und Zeit der ersten Beobachtung sind Eingaben in den Zellen G12 und G13 und werden dat und ot genannt. Damit liefert die in der Zelle N18 stehende Excel Formel
=TAGE(dat;ref)+ot-0,5
die Zeit T in Tagen als Dezimalbruch auf die Sekunde genau mit 7865,89505787037 Tagen. Dieser Zeit geben wir den Namen _T1. Damit können wir nun L, ![]() , e und
, e und ![]() in den Zellen N19, N21, N24 und N28 ausrechnen, indem wir einfach die Formeln aus der vorstehenden Tabelle im Excel Format in die entsprechenden Zellen hineinschreiben. So lautet die Formel für L einfach =_A1+_B1*_T1. Bei den anderen Bahnelementen ist das genauso simpel, weil die Bahnparameter in den Zellen K18 bis K26 die Namen _A1 bis _B4 erhalten haben. Die in Grad ausgerechneten Bahnelemente L,
in den Zellen N19, N21, N24 und N28 ausrechnen, indem wir einfach die Formeln aus der vorstehenden Tabelle im Excel Format in die entsprechenden Zellen hineinschreiben. So lautet die Formel für L einfach =_A1+_B1*_T1. Bei den anderen Bahnelementen ist das genauso simpel, weil die Bahnparameter in den Zellen K18 bis K26 die Namen _A1 bis _B4 erhalten haben. Die in Grad ausgerechneten Bahnelemente L, ![]() und
und ![]() werden jetzt ins Bogenmaß umgerechnet und in den darunter liegenden Zellen mit dem Index rad für Radiant abgelegt. Das geht in Excel ebenfalls sehr elegant mit der Formel Xrad = BOGENMASS(X), oder auch mit Xrad =X*PI()/180. In Excel und auch in allen anderen Programmiersprachen wird grundsätzlich im Bogenmaß statt in Graden gerechnet.
werden jetzt ins Bogenmaß umgerechnet und in den darunter liegenden Zellen mit dem Index rad für Radiant abgelegt. Das geht in Excel ebenfalls sehr elegant mit der Formel Xrad = BOGENMASS(X), oder auch mit Xrad =X*PI()/180. In Excel und auch in allen anderen Programmiersprachen wird grundsätzlich im Bogenmaß statt in Graden gerechnet.
Vielleicht wundern wir uns über den großen Winkel von L. Doch im Juli 2021 hat die Erde die Sonne etwa 21,5-mal mit je 360° umrundet und das wären dann knapp 21,5・360° = 7740° plus die 280° vom Frühlingspunkt bis zum Perihel und das wären dann 8020°. Die genaue Zahl liefert das Bahnelement L mit 8033,46412047325 in der Zelle N19 oder mit dem Bogenmaß von 140,2104 in der Zelle N20. Es hätte nur optische Gründe, wenn wir diese Ergebnisse auf den Hauptwinkel ![]() umrechnen würden, d. h., 22 Mal
umrechnen würden, d. h., 22 Mal ![]() bzw. 360° davon abzuziehen. Da wir diesen Winkel später nur in einer Tangensfunktion gebrauchen, muss das aus Gründen der Berechnung nicht gemacht werden, weil tan(x) = tan(x + n・2????) ist und n dabei beliebig groß sein kann.
bzw. 360° davon abzuziehen. Da wir diesen Winkel später nur in einer Tangensfunktion gebrauchen, muss das aus Gründen der Berechnung nicht gemacht werden, weil tan(x) = tan(x + n・2????) ist und n dabei beliebig groß sein kann.
Als nächstes kümmern wir uns um die Ellipsenform der Erdbahn. Dafür liefert uns C ein Maß, das die Abweichung der elliptischen Erdbahn von einer Kreisbahn beschreibt. Weil die Exzentrizität mit e = 0,0167 klein ist, kann C in einer Reihenentwicklung berechnet werden. Dazu braucht man die sog. mittlere Anomalie M, was hier nicht weiter vertieft werden soll, nur soweit, M ist die Differenz aus L und ![]() . Die Reihe konvergiert sehr schnell, so dass man nur die ersten drei Glieder ausrechnen muss. Die Formel dafür lautet:
. Die Reihe konvergiert sehr schnell, so dass man nur die ersten drei Glieder ausrechnen muss. Die Formel dafür lautet:
![]()
In Excel ist diese Formel schon etwas länger, als die vorhergehenden Excel Formeln, nämlich
=(2*N24-N24^3/4)*SIN(N23)+5*N24^2/4*SIN(2*N23)+13*N24^3/12*SIN(3*N23).
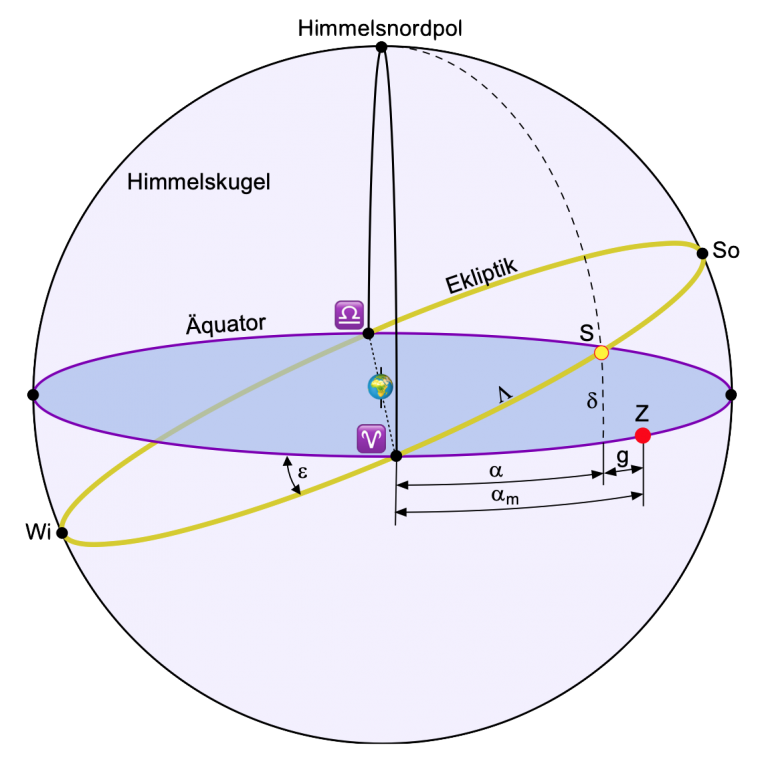
Damit kann die wahre Länge ???? ausgerechnet werden, die sich einfach als Summe der mittleren Länge L und C ergibt. Die mittlere Länge L ist der Weg, den eine Vergleichssonne Z längs des Himmelsäquators zurücklegt. Die wahre Länge ???? ist der Weg, den die wahre Sonne auf der schrägstehenden Ekliptik derselben Himmelskugel zurücklegt. Beide Sonnen haben dabei die gleiche Geschwindigkeit auf einem gleichgroßen Kreis. Sie haben auch zum selben Zeitpunkt den Frühlingspunkt ♈︎ passiert. Bild 5 zeigt das Ganze grafisch. Darin ist ![]() die verkürzte Länge von L, wie oben beschrieben und ???? ist die wahre, ebenfalls auf den Hauptwinkel verkürzte Länge. Wird der Ort der Sonne S längs ihres Himmelsmeridians auf den Himmelsäquator projiziert, dann entsteht ein rechtwinkliges Kugeldreieck, in dem die Länge von
die verkürzte Länge von L, wie oben beschrieben und ???? ist die wahre, ebenfalls auf den Hauptwinkel verkürzte Länge. Wird der Ort der Sonne S längs ihres Himmelsmeridians auf den Himmelsäquator projiziert, dann entsteht ein rechtwinkliges Kugeldreieck, in dem die Länge von ![]() berechnet werden kann. Die Differenz von
berechnet werden kann. Die Differenz von ![]() und
und ![]() liefert dann die Zeitgleichung g.
liefert dann die Zeitgleichung g.
In der Praxis macht die naheliegendste Gleichung zur Berechnung von
![]()
einige Schwierigkeiten bei der Berücksichtigung der Vollkreisigkeit. Deshalb ist hier eine andere Gleichung angebracht, die auch sofort die Zeitgleichung liefert. Durch Anwendung eines Tangens-Additionstheorems auf ![]() erhält man:
erhält man:
![]()
In Excel schreibt sich das als:
=ARCTAN( (TAN(N20)-TAN(N26)*COS(N28)) /(1+TAN(N20)*TAN(N26)*COS(N28)))
Mit der Kenntnis der Zeitgleichung ist es nun ganz einfach, den Greenwich Stundenwinkel auszurechnen. Dieser ist definiert als
![]()
Hierin ist die Zahl 0,261799 das Bogenmaß der Geschwindigkeit der Sonne von 15°/h (15・????/180). Die Sonne braucht 12 h, um von 180° E auf 0° nach Greenwich zu kommen. Deshalb müssen 12 h addiert werden. Wird (ot + 12 h) größer als 24 h, dann startet die Sonne ab Greenwich den nächsten Umlauf und es müssen 24 h abgezogen werden, also wenn (ot + 12 h) > 24, dann muss (ot – 12 h) gerechnet werden. In Excel schreibt man dafür:
=WENN((ot*24+12)>24;N29+BOGENMASS(15)*(ot*24-12);N29+BOGENMASS(15)*(ot*24+12))
Das Ergebnis steht in Zelle N30 als Grt0, denn es müssen noch eventuelle Überträge beachtet werden. Wenn es in Greenwich 12:00:00 UT1 ist, dann kann der Bildpunkt der Sonne auch mal auf Grt = 357° stehen, wofür die beiden vorstehenden Formeln dann -3° ausrechnen würden. In dem Fall, dass Grt0 negativ ist, müssen also 2???? addiert werden:
=WENN(N30<0;N30+2*PI();N30)
Wir haben jetzt den Grt im Bogenmaß und können ihn durch Multiplizieren mit 180/???? ins Winkelmaß umrechnen. In Excel geht das auch einfach mit der Formel = Grad(X) und schon erscheint der im Bogenmaß gegebene Winkel X im Gradmaß.
Die Berechnung der Deklination ???? ist jetzt super einfach. Wir haben, wie im Bild 5 gezeigt, die wahre Länge ???? und die Schräge ![]() eines rechtwinkligen Kugeldreiecks und wollen ???? ausrechnen. Das geht mit der Formel
eines rechtwinkligen Kugeldreiecks und wollen ???? ausrechnen. Das geht mit der Formel
![]() ,
,
die in Excel =ARCSIN(SIN(N26)*SIN(N28)) lautet. Auch hier kann der im Bogenmaß vorliegende Winkel ins Gradmaß umgerechnet werden, was grundsätzlich nur für Informationszwecke getan werden muss. Die folgende Standortberechnung arbeitet natürlich wieder mit den Bogenmaßen. Für die zweite Beobachtung gilt dann die zweite Spalte von O17 bis O34. Zur Unterscheidung sind dort die Variablen mit einem Apostroph gekennzeichnet.
Die erforderlichen Berechnungen für Grt und ???? sind also wirklich kein Hexenwerk, wenn dazu die richtigen Mittel eingesetzt werden. Sie ist mit 14 einfachen, in einem Durchgang zu berechnenden Formeln getan, wozu ein normaler Computer, wie ihn jeder zu Hause hat nicht mal eine Millisekunde braucht. Genauso einfach ist dann auch die Berechnung eines versegelten Standortes, was im nächsten Abschnitt dargelegt wird.
Die Gauß Methode
Johann Carl Friedrich Gauß war ohne Frage der berühmteste Mathematiker aller Zeiten. Er beschäftigte sich mit der Astronomie, aber auch mit der Landesvermessung. Dafür musste er auch Längengrade und Breitengrade bestimmen können.
Seit dem 16. Jahrhundert kennt man ein Dreiecksmodell, das aufzeigt, wie ein Standort aus zwei Höhen der Sonne oder anderer Gestirne bestimmt werden kann. Das Problem war nur, dass niemand eine Berechnungsmöglichkeit für den Standort angeben konnte, die einfach genug ist, dass sie auch auf See angewendet werden konnte. Für Mathematiker hingegen war es auch damals nicht unmöglich, Schritt für Schritt aus den gegebenen Elementen und langwieriger Rechenarbeit einen Standort zu berechnen.
Gauß ging einen anderen Weg, er betrachtete nicht die Zeichnung, sondern ein Gleichungssystem, welches das vorliegende Dreiecksmodell komplett beschrieb und ging dann mit den Mitteln der mathematischen Analyse vor. Das Ergebnis war ein Formelapparat, mit dem ein Standort aus nur zwei Gestirnshöhen einfach nur berechnet wird. Seine Formeln sind an Genialität nicht zu übertreffen. Doch leider verstand sie niemand, sie waren wie der Ansatz viel zu abstrakt und hatten überhaupt keinen Bezug mehr zu den einzelnen Elementen des ursprünglichen Dreiecksmodells. Es war halt pure Mathematik. Auch die Seeleute konnten damit nichts anfangen, auch weil zur Lösung immer noch zu viele Logarithmen nötig gewesen wären, was einfach auf eine viel zu langwierige Berechnung hinausgelaufen wäre.
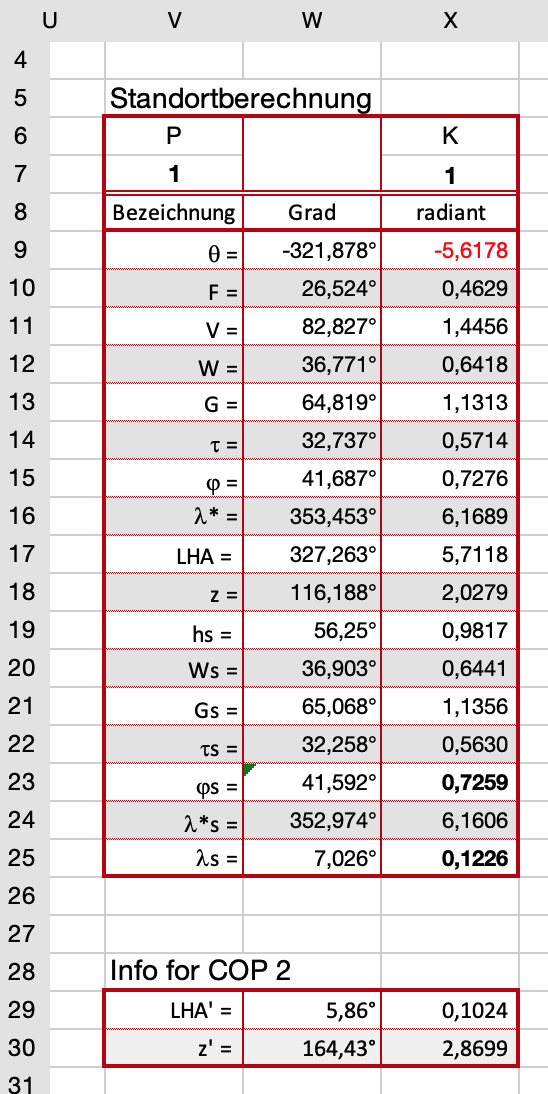
Mit Elektronenrechnern ist das heute kein Thema mehr. Die Tabelle im Bild 6. zeigt eine Excel Rechentabelle, die in 17 Zeilen eine komplette Standortberechnung mit Versegelung durch zweifache Anwendung des Formelsatzes bewerkstelligt.
In den Zellen V7 und X7 werden erstmal grundsätzliche Dinge betrachtet. Weil zwei sich überlappende Höhenkreise zwei mögliche Standorte zulassen, muss im Feld C8 angegeben werden, ob ein Standort nördlich oder südlich der Deklinationsbreite berechnet werden soll. Mit N (Nord) wird P = 1 und mit S (Süd) wird P = -1.
Die Konstante K ist zuständig für Beobachtungen an aufeinanderfolgenden Tagen. Kein Problem ist es, wenn die erste Beobachtung um 23 Uhr und die zweite um 1 Uhr am darauffolgenden Tag erfolgt. Das gibt es von uns aus gesehen auf der anderen Seite der Erde. Es existieren jedoch Zeitkonstellationen, die eine Vorzeichenumkehr erfordern und dafür ist die Konstante K mit 1 bzw. -1 zuständig. Beispielsweise wird eine erste Beobachtung erst um 19 Uhr möglich, weil der Himmel den ganzen Tag über bewölkt war und am Folgetag schaut die Sonne ganz kurz schon mal um 16 Uhr nur für wenige Minuten aus den Wolken hervor. Dann will man sich das nicht entgehen lassen und macht eine Beobachtung, obwohl die zweite Beobachtung dann tageszeitlich gesehen vor der ersten Beobachtung liegt. Doch mit der richtigen Vorzeichenanwendung mittels K ist das kein Problem. Die Basisformeln lauten in der Übersicht:
![]()
![]()
![Rendered by QuickLaTeX.com \[W=P\cdot\cos^{-1}\Bigg[\frac{\cos V\cdot\tan h}{\tan (F-\delta)}\bigg(\frac{\sin h'\cdot\sin F}{\sin h\cdot\sin \delta'\cdot\cos(F-\delta)}-1\bigg)\Bigg]\]](https://zephir-yacht.com/wp-content/ql-cache/quicklatex.com-fb9d04c8ae4da2ba93b448f6177086f4_l3.png)
![]()
![]()
![]()
Dabei ist:
![]()
Diese Formeln stehen als Excel Formeln in den Zellen X9 bis X15. Aus der jetzt bekannten Breite und dem Greenwichwinkel aus der ersten Beobachtung könnte jetzt auch eine Länge berechnet werden. Zuvor wollen wir aber noch eine Versegelung berechnen. Um das möglichst professionell zu erledigen, muss eine sog. Höhenanpassung vorgenommen werden. Dazu muss das Azimut berechnet werden, was in den Zellen X16 bis X18 gemacht wird. In der Zelle X20 erfolgt dann die Höhenanpassung:
![]()
Mit der auf den versegelten Standort angepassten Höhe hs wird dann der versegelte und damit aktuelle Standort berechnet, wozu die in den Zellen X10 bis X15 angewendeten Formeln kopiert und erneut angewendet werden, wobei in den kopierten Formeln h gegen hs auszutauschen ist. Jetzt werden ![]() und Grt addiert und man erhält den Längengrad. Dieser ist als Stundenwinkel angegeben und muss auf die geografischen Ostgrade und Westgrade umdefiniert werden. Es handelt sich um Westgrade, wenn das Ergebnis kleiner als ???? ist. Ist das Ergebnis größer als ????, dann ist es von 2???? abzuziehen und es sind Ostgrade. Die Umwandlung vom Bogenmaß in Grade für eine Ergebnisanzeige erfolgt sowohl für den Breitengrad, als auch für den Längengrad mit der Excel Formel =GRAD(x) oder durch Multiplikation mit 180/????.
und Grt addiert und man erhält den Längengrad. Dieser ist als Stundenwinkel angegeben und muss auf die geografischen Ostgrade und Westgrade umdefiniert werden. Es handelt sich um Westgrade, wenn das Ergebnis kleiner als ???? ist. Ist das Ergebnis größer als ????, dann ist es von 2???? abzuziehen und es sind Ostgrade. Die Umwandlung vom Bogenmaß in Grade für eine Ergebnisanzeige erfolgt sowohl für den Breitengrad, als auch für den Längengrad mit der Excel Formel =GRAD(x) oder durch Multiplikation mit 180/????.
Schiffsmittag
Der Ortsstundenwinkel LHA ist der Längengradunterschied vom Standortmeridian in westliche Richtung gehend bis zum Meridian des Bildpunkts. Rechnet man 360° – LHA, dann ist das umgekehrt der Längengradabstand, den die Sonne bis zum Schiffsort noch zurückzulegen hat. Teilen wir diesen Wert durch 15°/h, dann ist das die Zeit, bis der Bildpunkt den Meridian des Schiffsortes erreicht. Diese Zeit des Durchgangs der Sonne durch den Standortmeridian ist der Schiffsmittag. Man muss an Bord also immer (360° – LHA)/15° Stunden warten, bis Schiffsmittag ist. Daraus folgt dann, dass die Zeit des Schiffsmittags die aktuelle Uhrzeit plus dieser Wartezeit ist.
Mit Zeiten kann in Excel unterschiedlich kompliziert umgegangen werden. Weil dort per Definition 24 h = 1 d (Tag) sind, kann eine Tageszeit ganz einfach auch als Dezimalzahl formatiert werden. So steht in unserem Beispiel in der als Zeit formatierten Zelle G13 der Wert 9:28:53, die Zeit der ersten Beobachtung. Jetzt könnte man einfach diese Zelle per Mausklick auswählen und als Standardzahl formatieren rechte Maustaste; Zellen formatieren … – Zahlen – Standard. Dann steht in dieser Zelle die Zahl 0,39506. Das ist ebenfalls eine Zeitangabe und bedeutet 0,39506 Tag.
Die Wartezeit bis zum Mittag ist wie oben gezeigt (360° – LHA°)/15, also (360° – 327,3°)/15 h = 2,1825 h und das sind 2,1825/24 = 0,09094 Tag. Dazu wird jetzt die Beobachtungszeit von 0,39506 addiert und das Ergebnis ist 0,48599 d oder in Zeit formatiert 11:39:50 UT1. Die Excelformel in Zelle C26, die mit D26 verbunden ist lautet:
=(360-V17)/15/24+ot
die Variable ot in dieser Formel bedeutet Observationszeit der ersten Beobachtung.
Zusatzinformationen
Beim praktischen Gebrauch dieses Tools muss eigentlich niemand wissen, was die Begriffe Deklination, Greenwichwinkel oder Ortsstundenwinkel bedeuten.
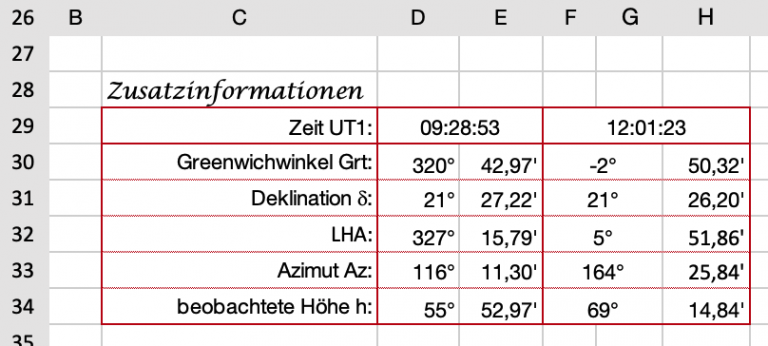
Ebenso muss niemand wissen, was ein Azimut ist oder worin der Unterschied zwischen der Sextantenablesung und einer beobachteten Höhe besteht. Trotzdem schadet es niemandem, davon etwas zu verstehen und deshalb werden diese Werte in einer kleinen Tabelle ausgegeben, die im Bild 8 dargestellt ist. Für den einen oder anderen ist es vielleicht interessant, wenn er diese Daten zu sehen bekommt.
Die Angaben in dieser Tabelle erfolgen alle, genau wie bei der Ergebnisanzeige in den Zellen C25 bis H25, in Grad und Minuten. Diese Angaben werden aus dem errechneten Dezimalgrad gewonnen.
Warnmeldungen
Manchmal kann es unbeabsichtigt zu Falscheingaben kommen. Wird das nicht sofort erkannt, dann kann es schon eine Menge Zeit rauben, bis der Fehler gefunden wird. Fehlerausschriften können hier ganz hilfreich sein. Wenn bei der Standortwahl statt N oder S fälschlicherweise W oder E eingegeben wird, dann erscheint im Feld C9 die Warnausgabe “N oder S eingeben”. Wird ein falscher Sonnenrand eingegeben, so z. B. H oder L dann erscheint im Feld H5 das wort “ERROR”. die Excel Formeln für diese Zellen lauten für die Zelle C9:
=WENN(ODER(C8=”N”;C8=”S”);” “;”N oder S eingeben”)
und für die Zelle H5:
=WENN(ODER(UND(H6=”O”;ODER(H7=”O”;H7=”U”));
UND(H6=”U”;ODER(H7=”O”;H7=”U”)))=WAHR;” “;”ERROR”)
Weitere Fehlerausschriften gibt es auch, wenn eine Uhrzeit falsch eingegeben wurde.
Namen und Formelzeichen
Die Symbole aus der Mathematik können nicht einfach in Excel übernommen werden. Beispielswese wird die Höhe aus zweiter Beobachtung in einer mathematischen Gleichung als h2 bezeichnet. Excel versteht darunter jedoch die zweite Zeile in der Spalte H. So muss man für fast alle mathematischen Symbole Excel-Namen festlegen und diesen dann bestimmte Zellen zuweisen. So kann man in den Zellenfunktionen einfach diese Namen verwenden und muss die Bezüge zu diesen Zellen nicht mehr als absolut definieren. Eine Aufstellung der Namen, Symbole, Bezeichnung und den Zellbezug der hier beschriebenen Navigationsdatei ist in der nachstehenden Tabelle aufgeführt.
| Name in Excel | math. Symbol | Bezeichnung | Zelle |
| _A1 bis _A2 | Orbitalkonstanten am 1. Jan 2000 | J18 – J21 | |
| _B1 bis _B2 | Orbitalkoeffizienten ab 1. Jan 2000 | J23 – J26 | |
| Az_° | Azimut Beobachtung 2 | U30 | |
| Az° | Azimut Beobachtung 1 | U18 | |
| B | Grafik, LHA° > 180° | M12 | |
| B_ | Grafik, LHA_° > 180° | M13 | |
| cmg | c | course made good in Grad | H17 |
| d | Deklination Beobachtung 1 | N32 | |
| d_ | Deklination Beobachtung 2 | O32 | |
| dat | Datum Beobachtung 1 | G12 | |
| dat_ | Datum Beobachtung 2 | G20 | |
| dmg | d | distance made good in NM | C17 |
| F | Hilfswinkel | V10 | |
| G | Hilfswinkel | V12 | |
| grt | Grt | Greenwichwinkel Beob. 1 | N31 |
| grt_ | Grt’ | Greenwichwinkel Beob. 2 | O31 |
| Gs | Hilfswinkel nach Versegelung | V21 | |
| h | h | beobachtete Höhe Beobachtung 1 | L13 |
| h_ | h’ | beobachtete Höhe Beobachtung 2 | N13 |
| h_° | beobachtete Höhe Beobachtung 2 in Grad | N11 | |
| h° | beobachtete Höhe Beobachtung 1 in Grad | L11 | |
| hs | hs | angepasste Höhe nach Versehelung | V19 |
| j | mittlere Breite | V15 | |
| js | Standortbreite | V23 | |
| K | K | Konstante 1 oder -1 | V7 |
| lat | Latitude nach Versegelung in Dezimalgrad | U23 | |
| lat° | Latitude vor Versegelung in Grad | U15 | |
| LHA | LHA | Ortsstundenwinkel Beob. 1 | V17 |
| LHA° | Ortsstundenwinkel Beob. 1 in Grad | U17 | |
| LHA°_ | Ortsstundenwinkel Beob. 2. in Grad | U29 | |
| lon | Longitude nach Versegelung in Dezimalgrad | U25 | |
| ls | Längengrad nach Versegelung | V25 | |
| ot | Tageszeit Beobachtung 1 | G13 | |
| ot_ | Tageszeit Beobachtung 2 | G21 | |
| q | Zwischenzeit in Grad | V9 | |
| ref | Referenzdatum 01.01.2000 | K28 | |
| tau | Stundenwinkel | V14 | |
| taus | Stundenwinkel nach Versegelung | V22 | |
| TG | Tage nach erster Beobachtung | F20 | |
| V | Hilfswinkel | V11 | |
| var |
Variable füe Falsch |
U6 |
|
| vb | Grafik, versegelte Breite | O9 | |
| vl | Grafik, versegelte Länge | O10 | |
| W | W | Hilfswinkel | V12 |
| Ws | Ws | Hilfswinkel nach Versegelung | WV20 |
| z_ | z’ | Azimut Beobachtung 2 | V30 |
Grafik
Das Gauß Verfahren liefert als Ergebnis nur die Standortkoordinaten als Zahlen. Wenn man eine Grafik haben möchte, dann müsste man den errechneten Standort mittels zusätzlicher Software als Schiffsymbol in eine elektronische Vektorkarte übertragen, so wie das in der Satellitennavigation gemacht wird. In Excel für Mac kann leider keine Karte eingebracht werden. Da gibt es nur die Möglichkeit, Grafiken in kartesischen Koordinaten darzustellen. Aber auch das kann interessant sein. Für die Grafik wurde ein zweites Arbeitsblatt verwendet.
Eine Grafik wird erzeugt, indem unter Verwendung aller Höhen, also der Höhen aus beiden Beobachtungen und der durch Versegelung angepassten Höhe Stücke der Höhenkreise berechnet werden. Dazu werden in einer Wertetabelle für jede Breite die zugehörigen Längen unter Verwendung der entsprechenden Höhen berechnet und in ein kartesisches zweidimensionales Diagramm gebracht. Nachteilig ist, dass dabei die Nord-Süd Achse nur horizontal dargestellt werden kann. Das Diagramm ist also um 90° nach rechts gekippt.
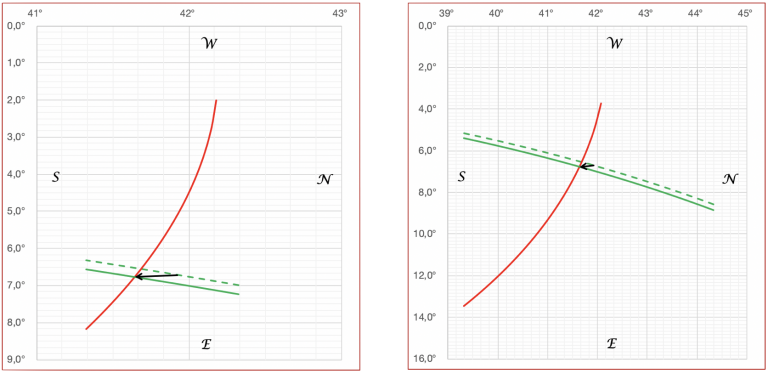
Unverkennbar ist, dass der Algorithmus keine Standlinien benutzt. Als Standort werden die tatsächlichen Kreuzungen der Höhengleichen berechnet. Die verschiedenen Farben bedeuten:
grün gestrichelt: Höhengleiche aus Beobachtung 1
grün: versegelte Höhengleiche aus Beobachtung 1
rot: Höhengleiche aus Beobachtung 2
schwarz: Versegelungsvektor (DMG & CMG)
Um eine solche Grafik zu machen, muss eine Wertetabelle erstellt werden. Für diese Wertetabelle muss der Rechner um ein Vielfaches mehr rechnen, als für die gesamte auf dem ersten Arbeitsblatt gezeigte Standortberechnung. Den Aufbau der Wertetabelle zeigt Bild 9.
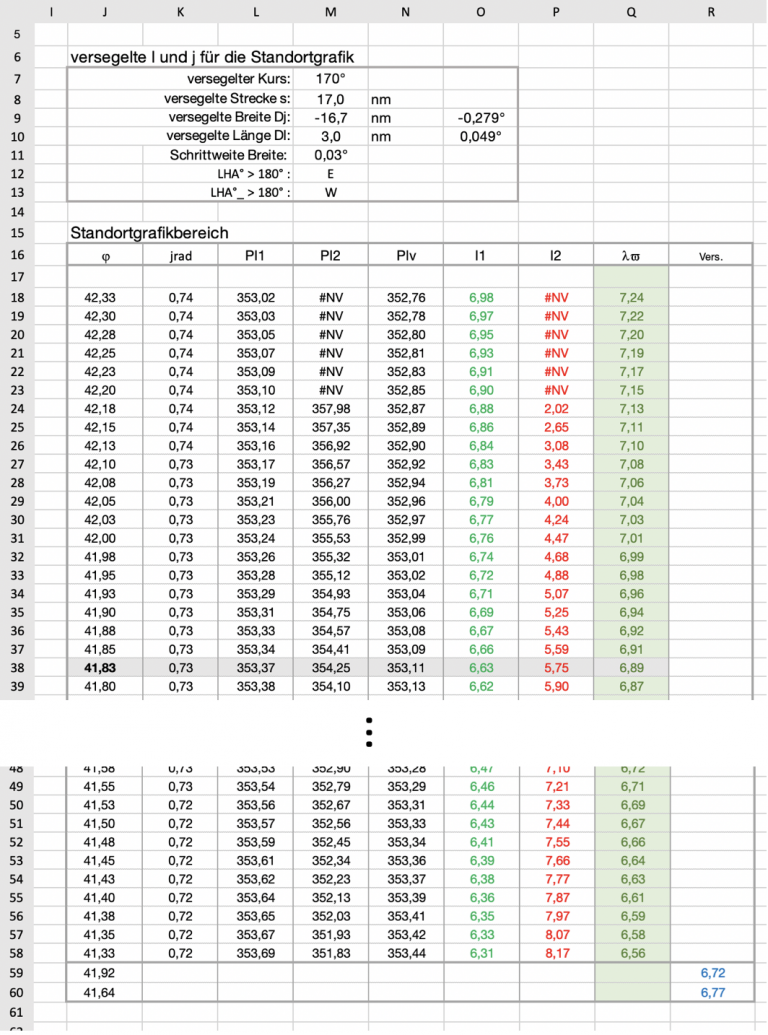
Ganz oben werden in einer kleinen Tabelle einige Basiswerte errechnet bzw. zusammengestellt. Das Vorgehen soll nicht näher kommentiert werden, da die verwendeten Formeln in der Datei eingesehen werden können. Nur soviel: Aus den Angaben von Kurs und Distanz müssen die versegelten Breiten und Längen in den möglichen Quadranten gefunden werden. In der Haupttabelle werden unter P wie Polwinkel zunächst die Stundenwinkel berechnet und daraus dann die Längen. Würde man gleich die Längen berechnen, dann würden die Excel Formeln recht lang und damit unübersichtlich werden. Die Variable #NV erscheint, wenn ein Polwinkel nicht lösbar ist, weil dann Längen berechnet werdensollen, für die es keine Breiten mehr gibt. Das ist immer nördlicher oder südlicher von einer Höhengleiche der Fall. Die mit #NV beschriebenen Zellen werden nicht zur Anzeige gebracht.
Arbeitsblätter schützen
Ein Schutz der Arbeitsblätter dient hier nicht der Geheimhaltung, sondern vielmehr dem Schutz der Datei vor einem selbst. Schnell ist in einer ungeschützten Datei der Inhalt einer Zelle überschrieben, die eine wichtige Formel beinhaltete. Die ist dann weg. Wenn Eingaben gemacht werden sollen, dann muss vor dem Blattschutz ausgewählt werden, welche Zellen nach einem Blattschutz beschreibbar bleiben sollen, denn man muss ja Datum, Uhrzeit, Sextanten Ablesung usw. eingeben können.
In der Beispieldatei sind das alle in der Eingaben Maske im Bild 2 grau hinterlegten Zellen und auf dem Arbeitsblatt Grafik die Zelle H5 zur Eingabe eines darzustellenden Breitenbereichs. Man geht folgendermaßen vor:
- gesamtes Arbeitsblatt auswählen (Dreieck in dem Feld oben links über der 1 und vor dem A anklicken)
- Bearbeiten; Zellen formatieren, Schutz – Haken bei Gesperrt und ausgeblendet setzen – OK
- alle beschreibbaren Zellen auswählen
- Bearbeiten; Zellen formatieren, Schutz – Haken bei Gesperrt und ausgeblendet entfernen – OK
Der Zellenschutz ist allerdings erst wirksam, nachdem auch das Arbeitsblatt geschützt wird. Zu diesem Zweck ist das Drop Down Menü “Überprüfen” aufzurufen und darin das Symbol “Blatt schützen”. In dem daraufhin erscheinenden Auswahlfenster muss ein Kennwort eingegeben und in der Zeile darunter wiederholt werden. Außerdem kann ausgewählt werden, welche Elemente geschützt werden sollen. Hier genügt ein Haken bei “Nicht gesperrte Zellen auswählen”.
Aus optischen Gründen sollten vor dem Schutz in den Arbeitsblättern die Spalten J bis V bzw J bis R ausgewählt und ausgeblendet werden. Dazu diese Bereiche markieren, mit rechter Maustaste irgendwohin klicken und ausblenden wählen. Eine so vorbereitete Datei kann anschließend auf ein Smartphone oder Tablet geladen werden. Dort muss natürlich Excel installiert sein. Auf dem Display erscheint dann nur die Eingaben Maske gemäß Bild 2, in der die erforderlichen Eingaben gemacht werden können.
Zur Standortbestimmung ist nichts weiter nötig, als Datum, Uhrzeit und Sextanten Ablesung zweier Beobachtungen der Sonne. Durch Eingabe von Distanz und Kurs einer Ortsveränderung zwischen den Beobachtungen, einer sogenannten Versegelung, wird die Genauigkeit erheblich besser. Diese sollte man durch Kopplung zwischen den Beobachtungen ermitteln. Die Grundeinstellungen dürften auch kein Problem darstellen. Die Augeshöhe ist von der Standhöhe auf dem Boot abhängig. Ob man nördlich oder südlich der Deklinationsbreite segelt wird wohl jeder wissen. Die Indexberichtigung findet man durch Beobachtung des Horizonts, wobei in den Strahlengang des Indexspiegels das schwächste Filter oder gar kein Filter eingeschwenkt wird. Man sieht dann zwei übereinanderliegende Horizonte, die mit der Mikrometerschraube in Deckung zu bringen sind. Der Wert der danach abgelesen werden kann ist der Indexfehler. Einzutragen ist die Berichtigung dieses Fehlers, also sein negativer Wert. Doch das ist die einzige Rechenaufgabe, die bei der Verwendung dieses Tools noch gemacht werden muss – eine Vorzeichenumkehr.
Was noch zu sagen wäre
Das war jetzt mal eine ganz andere Methode zur Standortberechnung, als sie die heutigen Segelschulen immer noch vermitteln wollen. Ein nautisches Jahrbuch und all die anderen Utensilien sind auch nicht mehr nötig. Das ist eben der Vorteil der sehr viel älteren analytischen Methoden, die jedoch nur mit Computern nutzbar sind. Verwunderlich ist allerdings, dass man nicht gleich mit der Verbreitung des Computers darauf zurückgegriffen hat und dadurch eine ganze Generation von Schülern sich mit dem grafischen Höhenverfahren von Saint Hilaire herumplagen musste.
Die Gauß Methode ist in der nautischen Literatur nicht überliefert und nur als Faximile der Originalveröffentlichung von 1812 zu bekommen. In der moderneren Literatur findet man hin und wieder eine Methode beschrieben, mit der ein Standort direkt aus den Höhengleichen berechnet werden kann. Das ist eine sehr alte Methode, deren Anfänge sogar auf den Portugiesen Pedro Nunes (1502 bis 1578) zurückgeführt werden können.
Die Aufgabe, den Breitengrad aus den Höhen der Sonne zu zwei unterschiedlichen Zeiten zu bestimmen, ist als Zweihöhenproblem in die Geschichte der Navigation eingegangen und hat im Laufe der Zeit unzählige Lösungsvorschläge hervorgebracht. Dabei ging es gar nicht mal darum, überhaupt eine Lösung zu finden. Es ging vielmehr darum, mit einer Lösung den praktischen Anforderungen auf einem damaligen Segelschiff gerecht zu werden. Eine sehr alte genaue Berechnung stammt beispielsweise von Leonhard Euler und damit lange vor Gauß.
So war Gauß nicht der Erste, der das Problem der doppelten Höhen löste, wie oft gesagt wird. Er löste das Zweihöhenproblem vielmehr auf eine neue und damals höchst ungewöhnliche Weise, durch Anwendung der mathematischen Analyse. Neben der Breite war die Länge als Nebenprodukt gleich in seiner Lösung enthalten. Was Gauß jedoch präsentierte, war den Seefahrern absolut suspekt. Konnte man Formeln trauen, die durch mathematische Umwandlungen entstehen, die niemand nachvollziehen konnte? Etwa nach der Devise: “Das kann man nicht erklären, das kann man nur berechnen.” Jedenfalls ist das Hintergrundwissen dieser Methode bis zum heutigen Tage nicht anschaulich vermittelbar und deshalb wurde Gauß in der Seefahrt nie benutzt. Dass man Dinge nur berechnen kann, ohne sie erklären zu können, gehört heute durchaus zur Realität. Gauß war seiner Zeit viel zu weit voraus.
links:
nach oben ♦ Die Sonne am Himmel ♦ Mittagsbreite und Chronometerlänge ♦ Gauß und das Zweihöhenproblem ♦ Thomas H. Sumner, Begründer der Standliniennavigation ♦ Die Methode des Marcq Saint Hilaire ♦ Ein wenig Sextantenkunde ♦ Sextantentest Mark 25 ♦ Downloads ♦ Home